CSCI 3022 Intro to Data Science
Midterm Exam
数据科学代考 Multiple choice problems 1. (3 points) Consider the data set: [4, 10, 9, 19, 0, x], where x ∈ R is an unknown quantity.
Read the following:
- RIGHT NOW! Write your name, student ID and section number on the top of your exam. If you’re handwriting your exam, include this information at the top of the fifirst page!
- You may use the textbook, your notes, lecture materials, and Piazza as resources. Piazza posts should not be about exact exam questions, but you may ask for technical clarififications and ask for help on review/past exam questions that might help you. You may not use external sources from the internet or collaborate with your peers.
- You may use a calculator or Python terminal to check numerical results.
- If you print a copy of the exam, clearly mark answers to multiple choice questions in the provided answer box. If you type or hand-write your exam answers, write each problem on their own line, clearly indicating both the problem number and answer letter.
- Mark only one answer for multiple choice questions. If you think two answers are correct, mark the answer that best answers the question. No justifification is required for multiple choice questions. For handwriting multiple choice answers, clearly mark both the number of the problem and your answer for each and every problem.
- For free response questions you must clearly justify all conclusions to receive full credit. A correct answer with no supporting work will receive no credit.
- When submitting your exam to Gradescope, use their submission tool to mark on which pages you answered specifific questions. Submitting your exam properly is worth 1/100 points. The other problems sum to 99.
Multiple choice problems
1. (3 points) 数据科学代考
Consider the data set: [4, 10, 9, 19, 0, x], where x ∈ R is an unknown quantity. What is the smallest set of possible values that the median of this data set must belong to?
A. (−∞, ∞)
B. [6.5, 9.5]
C. 9
D. [0, 19]
E. {4, 9, 10}
F. ∅
2.(3 points)
Suppose Zach has a list consisting of all the fifirst generation Pok´emon and their types (Water, Ground, Fighting, etc.). He is conducting a study of how many of them are actually stronger than Mudkip – the cutest Pok´emon ever – by drawing a sample from his Pok´edex, which he has sorted alphabetically. He writes a loop that will randomly pick two Pok´emon of each type and compares those selected Pok´emon’s statistics to Mudkip’s. What type of sample did Zach collect?
A. Simple random sample
B. Systematic sample
C. Census sample
D. Stratifified sample
E. Free samples, all you can eat!
3.(3 points) 数据科学代考
Consider performing a simulation experiment where we record whether or not the events A and B happened. We perform the experiment n times, and store whether or not the events occurred each time into logical vectors of length n. What does the code below calculate?
def CountOutcomes(eventA,eventB): return np.sum(np.logical_and((eventA==True),(eventB==True))) / np.sum((eventA==True))
A. P(A ∪ B)
B. P(A ∩ B)
C. P(A|B)
D. P(B|A)
E. P(both flflips are heads)
4.(3 points) 数据科学代考
We’re considering a random variable to describe major earthquakes (above 8 Richter). We want to count how many such earthquakes occur per year. What variable is most appropriate?
A. Binomial
B. Negative binomial
C. Uniform
D. Normal
E. Poisson
F. Exponential
Use the following information for Problems 5 – 7, which may build offff of each other.
Ani (A) has run out of interesting games to play over quarantine, and now is stuck playing a rather bland variant of Snakes and Ladders with Blaine (B). In this game, each player tries to escape a maze.
Suppose that in general, Ani escapes 40% of the time and Blaine escapes 35% of the time.
5.(3 points)
Both players are able to escape in 1/4 of the games played. What is the probability that neither escape?
A. 1/10 B. 3/20
C. 1/6 D. 1/5
E. 1/4 F. 1/2
G. 3/4 H. 4/5
I. 5/6 J. 17/20
K. 19/20
6.(3 points) 数据科学代考
Suppose that Ani fails to escape. Now what is the probability that Blaine escapes?
A. 1/10 B. 3/20
C. 1/6 D. 1/5
E. 1/4 F. 1/2
G. 3/4 H. 4/5
I. 5/6 J. 17/20
K. 19/20
7.(3 points)
What is the probability that exactly one of them escapes?
A. 1/10 B. 3/20
C. 1/6 D. 1/5
E. 1/4 F. 1/2
G. 3/4 H. 4/5
I. 5/6 J. 17/20
K. 19/20

9. (3 points)
Suppose when you get to the cafeteria, you and your best friend have a competition to determine who gets the sushi rolls. You each type np.random.rand() into a terminal, and the person who gets the higher number wins and gets a sushi roll. You play the game until all 7 available sushi rolls are claimed. What is the probability that you get 5 or more of them?

10.(3 points) 数据科学代考
Suppose we have a real-valued random variable with pdf/pmf f and cdf F. Consider each function where we input an outcome x. Which of the following can be said about the relative magnitudes of f(x) and F(x)?
A. f(x) ≥ F(x) for both discrete and continuous random variables.
B. f(x) ≥ F(x) for discrete but not continuous random variables.
C. f(x) ≥ F(x) for continuous but not discrete random variables
D. F(x) ≥ f(x) for both discrete and continuous random variables.
E. F(x) ≥ f(x) for discrete but not continuous random variables.
F. F(x) ≥ f(x) for continuous but not discrete random variables.
G. None of the above are always true.
11.(3 points) 数据科学代考
Suppose we have a discrete rv X with pdf f. We then decide to take X and compute Z = X² + 2X + 1. Which of the following represent the expected value of Z?
A. E[X]² + 2E[X] + 1
B. E[(X + 1)²]
C. V ar[X]
D. V ar[X] + 2E[X] + 1
E. V ar[X] + (E[X] + 1)²
F. Stdev[X] + 2E[X] + 1
Free Response problems
12.(20 points) 数据科学代考
No justifification is necessary for this problem. Consider the given seven box plots, each from a data set with exactly 15 elements. Three of the data sets were generated by:
A = np.linspace(0,1,15) B = [x**3 for x in np.linspace(0,1, num=15)] C = [0,0,0,0,0,0,0,0,0,.1,.2,.3,.4,.5,1.0]
(a) (5 points) Match each of the three given data sets to their boxplot (box-whisker plot). Use the conventions from lecture, and clearly mark the number corresponding to your choice of boxplot in the boxes below for each data set. No boxplot is used more than once, and some are not used.
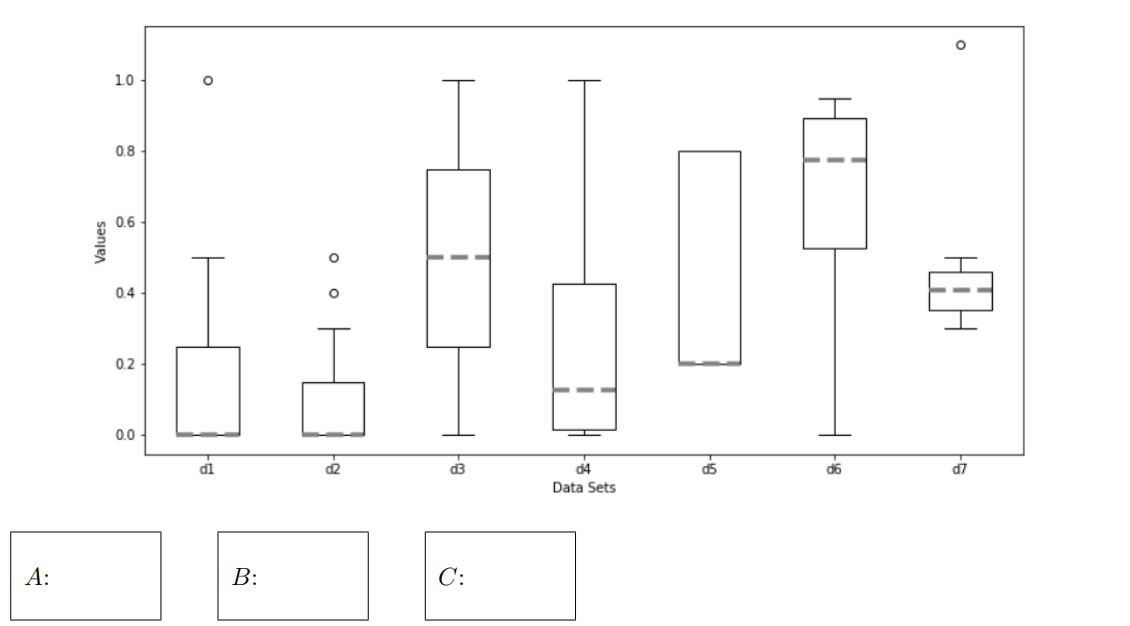
(b) (5 points) For the data sets labeled d2, d3 and d6 in the image above, characterize the data set as symmetric, right-skew, or left-skew. No justifification needed.
d2:
d3:
d6:
(c) (4 points) Some of the data sets in question have repeated observations, where the same data value occurs multiple times. Using only the boxplots shown, which of the 9 data sets must have repeated observations in them? Explain why.
(d) (3 points) Is the mean of d1 or d2 likely to be higher? Explain.
(e) (3 points) The data sets above were meant to represent possible observations of probabilities or proportions. Could any of the data sets above not have been proportion data? Why or why not?
13.(10 points) 数据科学代考
In order to get a little stress relief, we’re volunteering for the humane society, which is currently sheltering 23 puppies (P) and 14 kittens (K). The adorable creatures usually put us in a good mood (G), to the degree that we end up having a good time if we’re petting a puppy 85% of the time and we end up having a good time 70% of the times we’re petting a kitten.
Suppose on a Monday we’re assigned one of the available pets at random to play with when we enter the humane society.
(a) (6 points) After we’re done, we reflflect on our time and realize we didn’t actually have a good time. What’s the probability that the random pet we were assigned was a puppy?
(b) (4 points) Are the events P(G|P) and P(G) independent? Justify your response.
14.(16 points) 数据科学代考
Suppose whenever you roll a six-sided die and it comes up as a ”2”, you yell the word ”deuces” as loud as you can. You enjoy this activity so much that you manufacture a biased die. This die rolls a two 2/3 of the time, with each other other outcome equally likely.
(a) (4 points) What is the probability mass function for the face of the die?
(b) (4 points) What is the probability that it takes you 5 rolls before you can yell “deuces” twice?
(c) (4 points) What is the expected value of the face of the die after rolling?
(d) (4 points) What is the expected value of the square root of the face of the die after rolling?
15.(20 points) 数据科学代考
Consider a random variable X given by probability density function f(x) = ax(3 − x)² on the region x ∈ (0, 3) with an unknown constant a.
(a) (4 points) Sketch the pdf of X on a standard Cartesian axis, labeling any important features.
(b) (4 points) Find the value of a that will make f a proper pdf. Use this value for the rest of the problem.
(c) (3 points) Calculate E[X].
(d) (3 points) Calculate the cumulative density function for X.
(e) (3 points) Calculate V ar[X].
(f) (3 points) Is the median for x greater than or less than its mean? You may compute exactly or explain your result graphically.

