Data 102, Spring 2022 Midterm 2
数据期中代考 1.(7 points) For each of the following, determine whether the statement is true or false. For this question, no work will be graded and no partial
- You have 110 minutes to complete this exam. There are 7 questions, totaling40 points.
- You may use one 8.5 ×11 sheet of handwritten notes (front and back), and the provided reference sheet. No other notes or resources are allowed.
- You should write your solutions inside this exam sheet.
- You should write your name and Student ID on every sheet (in the provided blanks).
- Make sure to write clearly. We can’t give you credit if we can’t read your solutions.
- Even if you are unsure about your answer, it is better to write down partial solutions so we can give you partial credit.
- You may, without proof, use theorems and facts that were given in the discussions or lectures, but please cite them.
- There will be no questions allowed during the exam: if you believe something is unclear, clearly state your assumptions and complete the question.
- Unless otherwise stated, no work or explanations will be graded for multiple-choice questions.
- Unless otherwise stated, you must show your work for free-response questions in order to receive credit.
| Last name | |
| First name | |
| Student ID (SID) number | |
| Calcentral email
(@berkeley.edu) |
|
| Name of person to your left | |
| Name of person to your right | |
| Row (main exam room only) |
Honor Code: I will respect my classmates and the integrity of this exam by following this honor code. I affirm that all of the work submitted here is my original work, and I did not collaborate with anyone else on this exam.
Signature:______________________________________________________________
1.(7 points) 数据期中代考
For each of the following, determine whether the statement is true or false.
For this question, no work will be graded and no partial credit will be assigned.
(a) (1 point) In a k-armed bandit setting, the first k rounds of the UCB algorithm pull different arms.
○ A. TRUE ○ B. FALSE
(b) (1 point) Consider a k-armed bandit setting where one arm has an expected reward of 1 and all other arms have expected reward of 0. In this setting, the pseudo-regret of any algorithm is equal to the number of rounds where it selects an arm with expected reward of 0.
○ A. TRUE ○ B. FALSE
(c) (1 point) The stable unit treatment value assumption (SUTVA) requires that the potential outcomes are conditionally independent of the treatment.
○ A. TRUE ○ B. FALSE
(d) (1 point) When evaluating the causal relationship between a treatment Z and outcome Y , suppose that variable T is not directly caused by Z or Y (in other words, it is not a child of either in the causal DAG). T can still be a collider.
○ A. TRUE ○ B. FALSE
(e) (1 point) Random Forests are more interpretable than linear regression because their decisions can be expressed as majority votes of other classifiers.
○ A. TRUE ○ B. FALSE
(f) (1 point) An advantage of using random forests over decision trees is that they have lower variance.
○ A. TRUE ○ B. FALSE
(g) (1 point) In order to have good prediction accuracy with a two-layer neural net with prediction y = W1σ(W2x + b2) + b1, we must assume that the data are generated using that same process.
○ A. TRUE ○ B. FALSE
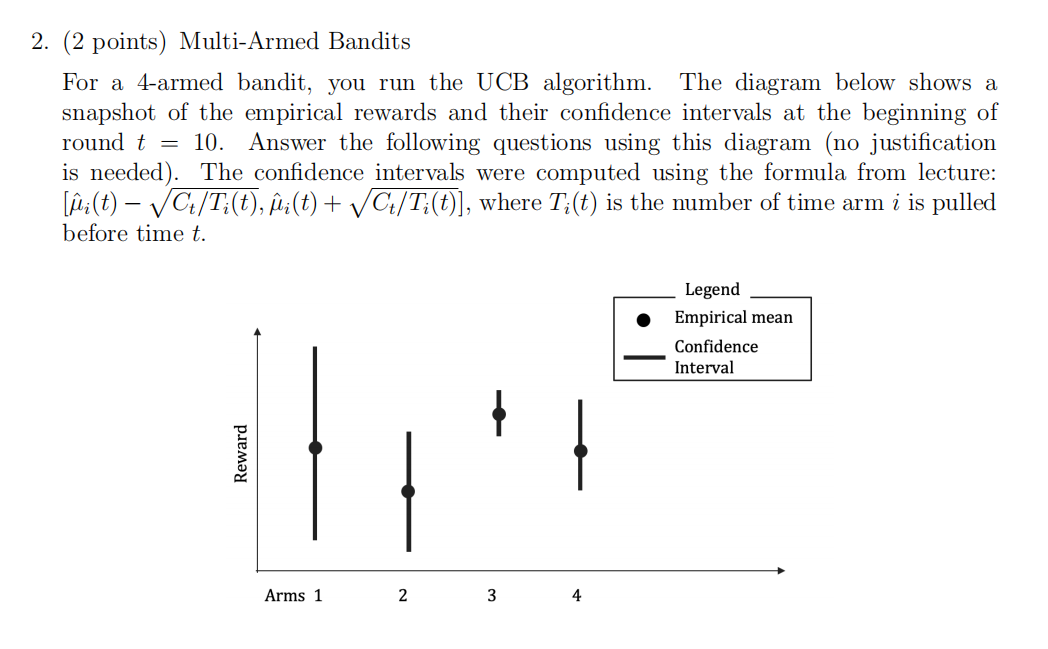
(a) (1 point) Which arm has been pulled most often by UCB up to time t = 10?
(b) (1 point) Which arm will be pulled by UCB at round t = 10?
3.(6 points) 数据期中代考
Consider an MDP with five adjacent states. The far left and far right states are terminal states, and the center state is the start state. The reward for entering each
state is as follows:
| 10 | 1 | 0 | -4 | 1000 |
There are two actions, left and right. Assume that the actions are deterministic: they move to the left one square and to the right one square respectively. Unless otherwise stated, assume that the discount factor is γ = 0.5.
(a) (2 points) Compute the optimal value function for the starting state, V*(start).
You do not need to simplify your answer arithmetically.
Hint: you don’t need to compute the value function for all states.
(b) (2 points) For this part only, we change the discount factor to γ = 1. In this case, what is the optimal policy? Give your answer by filling in the empty squares below with a left arrow for the left action and a right arrow for the right action. Briefly justify your answer.
| × | × |

4.(5 points)
Neural Networks and Backpropagation
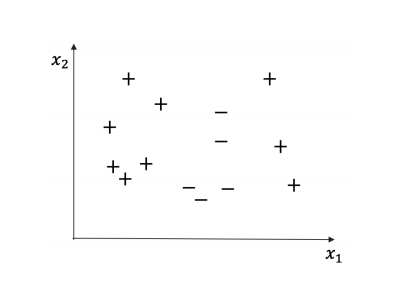
(a) (2 points) Consider a neural network with a sigmoid activation function at every hidden node and at the output (similar to what you saw in lecture). In order to achieve perfect classification accuracy on the dataset shown below, what is the smallest number of hidden layers needed? Briefly justify your answer. You don’t need to compute the weights of the network; just explain how many hidden layers and why.
(b) (1 point) Consider the following function to predict y from x: y = θ1sin(θ2x + θ3). Draw a computational graph for this function.
(c) (2 points) When computing the gradients of the function from the previous part (with respect to θ1, θ2, and θ3), which of the following is equal to the number of partial derivatives that must be computed when applying backpropagation? Choose the single best answer by filling in the circle next to it.
○ A. The number of nodes in the graph
○ B. The number of edges in the graph
○ C. The number of nodes on the path from x to y
○ D. The number of edges on the path from x to y
○ E. n1 + n2 + n3, where ni is the number of nodes on the path from θi to y.
○ F. e1 + e2 + e3, where ei is the number of edges on the path from θi to y.
5.(9 points) 数据期中代考
Matei is investigating whether watching Netflix causes lower grades. He finds data from a study that followed 1000 students for a semester, with the average number of hours they watched Netflix per week (W), their GPA (G), and whether they had high-speed internet (H). A separate study (not shown here) found that having high-speed internet caused students to earn higher grades.
W G H
1 3.4 1
15 3.7 1
15 2.9 0
(a) (2 points)
For this part only, assume that the data come from a randomized experiment, where each student was randomly assigned to watch either 1 or 15 hours per week. Matei wants to know the average treatment effect (ATE) of watching Netflix for 15 hours/week versus 1 hour/week on GPA. Assuming that the dataframe above is called netflix, either write 1-4 lines of code to compute an unbiased estimate for the ATE, or explain why this is impossible from the information given.
For the remainder of the question, we assume the data come from an observational study. Matei creates a new column Wb that is 0 if W ≤ 10 and 1 if W > 10.
He calls these categories “light watching” and “heavy watching” respectively, and wants to investigate whether heavy watching causes lower GPA than light watching.
(b) (2 points) 数据期中代考
Matei computes the average GPA for heavy watching students (3.4) and for light watching students (3.1), and incorrectly concludes that heavy watching causes students’ GPA to increase by 0.3 compared to light watching.
Which of the following statements are reasons that Matei’s conclusion (bolded above) is incorrect?
□ A. High-speed internet is a confounder for the treatment (light/heavy watching) and the outcome (GPA).
□ B. High-speed internet is a collider for the treatment (light/heavy watching) and the outcome (GPA).
□ C. Hours of Netflix watched and GPA could have a nonlinear relationship.
□ D. Choosing a threshold of 10 hours violates the stable unit treatment value assumption (SUTVA).
(c) (3 points) 数据期中代考
Matei finds out that Netflix randomly offered a free promotion (P) to half the students in the data: they were given $100 if they watched more than 10 hours a week during the semester.
Matei decides to use the promotion as an instrumental variable (IV). For each assumption required to use IVs, explain why the promotion does or doesn’t satisfy it. You should draw a causal DAG with the variables Wb, H, G, and P to support your answer.
(d) (2 points)
Matei decides to use inverse propensity weighting (IPW). He computes the IPW estimate for the ATE, removing points with propensity scores below 0.1 and 0.9 (as in Lab 8). Assume all necessary assumptions for using IPW are satisfied, and that he implements it correctly.
Now, he wants to quantify the uncertainty in his estimate. Is bootstrap appropriate?
Select all answers that apply.
□ A. Yes, because the IPW estimate is not sensitive to removal/inclusion of a small number of points.
□ B. No, because the IPW estimate is not sensitive to removal/inclusion of a small number of points.
□ C. Yes, because the random sampling in bootstrap eliminates the effect of any confounding variables.
□ D. No, because the random sampling in bootstrap eliminates the effect of any confounding variables.
□ E. No, because the number of parameters in the IPW estimate is equal to the number of data points.
□ F. None of the above
6.(6 points) 数据期中代考
Kaiea wants to predict the number of views that his YouTube videos will get. For each of his past videos, he collects the number of views, the time he spent creating it (in hours), its length (in minutes), and the number of guest stars. He builds the following dataframe, and applies negative binomial regression.
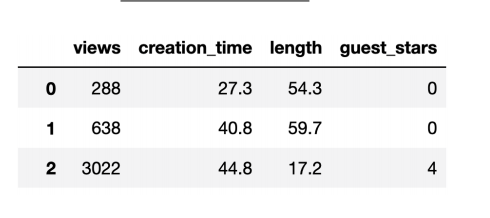
(a) (3 points) Bayesian: He implements the model correctly in PyMC3 and visualizes the coefficient posterior distributions (not all are shown):
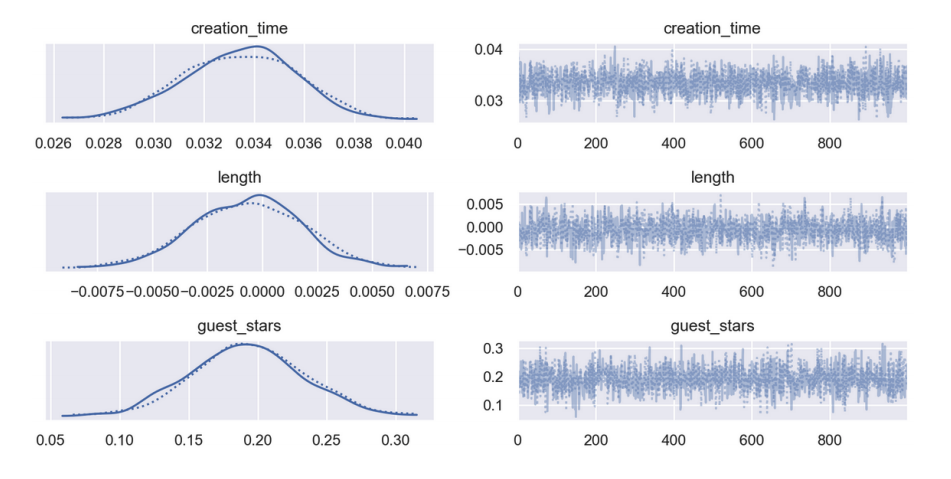
Which of the following are valid conclusions from these plots? Select all answers that apply.
□ A. Using a 99% credible interval for the coefficient of length, according to the model, longer videos are associated with more views.
□ B. Using a 99% confidence interval for the coefficient of length, according to the model, longer videos are associated with more views.
□ C. According to the model, each additional guest star is associated with an increase of between 0.05 and 0.35 additional views.
□ D. According to the model, adding one guest star is associated with the same effect on the number of views as spending an additional T hours making the video, and T is between 5 and 7.
(b) (3 points)
Frequentist: He implements the model correctly in statsmodels and obtains the following results:
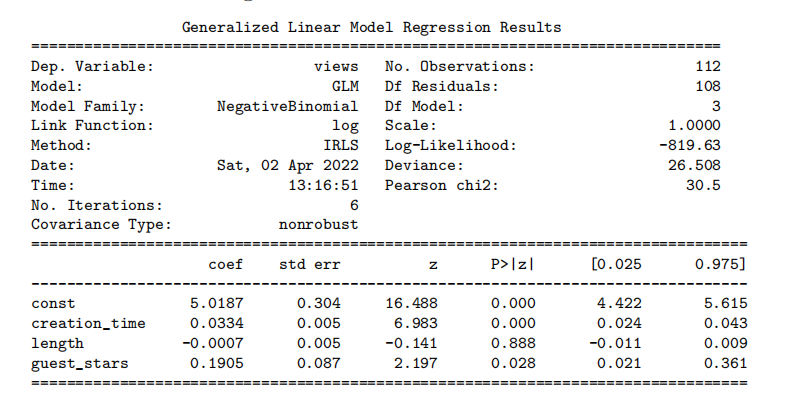
Which of the following are valid conclusions from these results? Note that the choices are the same as in the previous question, except for the numbers in choice C. Select all answers that apply.
□ A. Using a 99% credible interval for the coefficient of length, according to the model, longer videos are associated with more views.
□ B. Using a 99% confidence interval for the coefficient of length, according to the model, longer videos are associated with more views.
□ C. According to the model, each additional guest star is associated with an increase of between 0.021 and 0.361 additional views.
□ D. According to the model, adding one guest star is associated with the same effect on the number of views as spending an additional T hours making the video, and T is between 5 and 7.

(a) (2 points) Ritvik wants to know the probability of winning big, and decides to use Markov’s inequality with S50. He computes that E[S50] = 100, and writes down the following calculation: Pr(S50 ≥ 1000) ≤ 100/1000, but Ruhi points out that this isn’t correct. Explain to Ritvik why and where he made a mistake.
(b) (3 points) Ritvik decides to play at a table with limits on the bets, so that he can assume Xi is bounded between largest p for which Pr(S50 > 75) − ≥ 10 and 10. Given the information so far, find the p using what you learned in Data 102.


