Math 574
Midterm # 2: due April 19
数学Midterm代考 Let (xi, yj)0≤i,j≤N be uniform grids discretize the domain Ω and Let Uij de- note the approximation of u at point (xi, yj) and Fij = f (xi, yj).
Problem 1. Consider finite difference method to solve the Laplace prob- lem
−uxx − uyy = sin(πx) sin(πy) in Ω = (0, 1)2,
and
u = 0 on the boundary ∂Ω.
Let (xi, yj)0≤i,j≤N be uniform grids discretize the domain Ω and Let Uij de- note the approximation of u at point (xi, yj) and Fij = f (xi, yj).
a)Writedown the finite difference method for solving the Laplace equation above.
b)In MATLAB implementation, we use the command
U = zeros(N+1, N+1); 数学Midterm代考
to generate an initial guess of (U 0 )0≤i,j≤N to approximate u(xi, yj). To solve for Uij satisfies part a), write down a Gauss-Seidel iteration to generate a
U(kij≈ Uij .
c)In MATLAB code, we use the command
f = @(x,y) sin(pi*x).*sin(pi*y);
to define the function f (x, y) = sin(πx) sin(πy) and use the command
[X,Y] = meshgrid(0:h:1); F = f(X,Y);to generate Fij = f (xi, yj). Implement the Gauss Seidel iteration in part b). Set the tolerance tol = 1e-9, and
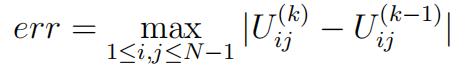
stop the iteration if err < tol. To plot the approximation U , use the com- mand
surf(X,Y,U)

d)For N = 8, 16, 32, record the number of the GS iteration in part c) and theerror 数学Midterm代考
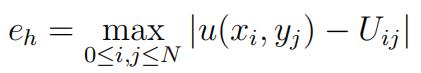
Note that the exact solution u(x, y) = 1 sin(πx) sin(πy).
e)Now suppose that the error eh≈ Chα for some constants C and α. Then
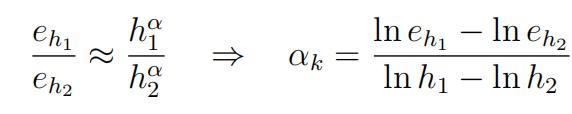
How do the values of α computed in part (d) compare to the rates of con- vergence for these norms predicted by the theory? Make sure to hand in a copy of your program as m file and the values you computed of e1/8, e1/16, e1/32 and α.
Problem 2. a) Write a computer program to approximate the solution of the boundary value problem: 数学Midterm代考
−u” + u = 1, 0 < x < 1, u(0) = 0 u(1) = 1.
by the finite element method using continuous piecewise linear elements on a uniform mesh of width h. Use h = 1/100 and 1/200.
b)Let uI(x) denote the piecewise linear interpolant of u, e., the piecewise linear function satisfying
uI(xi) = u(xi), i = 0, · · · , N, and e(x) = uI(x) − uh(x).
Let
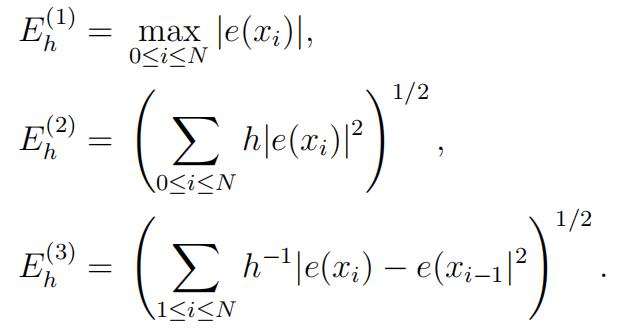
Have the computer determine E(1), E(2), E(3), for h = 1/100 and 1/200.
Note: the true solution of the boundary value problem is given by
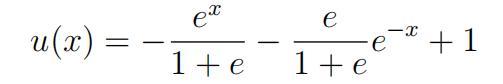
c)Now suppose that the error E(k)≈ Ckhαk for some constants Ck andαk.The error Eh gives an approximation to “u − uh“L2(0,1) and the errorEh gives an approximation to “∇(u − uh)“L2(0,1). How do the values of α2and α3 computed in part (c) compare to the rates of convergence for thesenorms predicted by the theory? Make sure to hand in a copy of your program as m file and the values you computed of E1/100, E1/200, and α.

更多代写:美国本科computer science论文代写 雅思代考 商科Online exam代考 美国essay写作 论文apa代写 代写的风险
