数学math代写 MT4516代写 Mathematics代写

School of Mathematics and Statistics MT4516 Finite Mathematics

数学math代写 (ii) If G is a generator matrix for C then G is a parity check matrix for C⊥.(iii) If C has dimension m then C⊥ has dimension n − m.

1.Consider the linear code C given by the parity check matrix  数学math代写

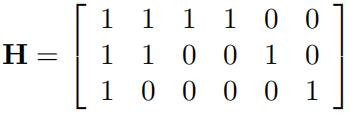
Use syndromes and coset leaders to decode the received words: 110001,111011 and 001110 .

2.Let C be a binary code with generator matrix

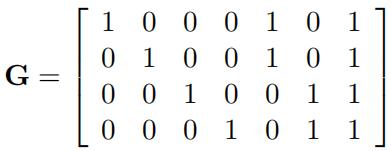
(i) Find a parity check matrix for C.

(ii) Compute the syndromes of the words 0000000, 1000000, 0010000, 0000100, 0000010, 0000001, 1000010, 0000110. Prove that they are coset leaders.

(iii) Decode the following received words: 1101011, 0110111, 0111000.

3.For x, y ∈ Zⁿ₂ , with x = x1x2 . . . xn and y = y1y2 . . . yn, defifine the dot product of x and y by  数学math代写

x · y = x1y1 + x2y2 + · · · + xnyn.

Prove that this operation satisfifies

x · y = y · x, x · (y + z) = x · y + x · z.

For a linear code C ⊆ Z ⁿ₂ , defifine its dual by

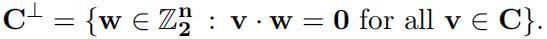
Prove the following statements.

(i) C^⊥ is a linear code.

(ii) If G is a generator matrix for C then G is a parity check matrix for C^⊥.

(iii) If C has dimension m then C^⊥ has dimension n − m.

(iv) If H is a parity check matrix for C then H is a generator matrix for C^⊥.

4.Let C be the code with parity check matrix

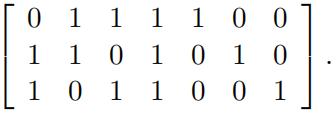
For each x = x1 . . . x7 ∈ C defifine x = x1 . . . x7x8 ∈ Z⁸ ₂ , where 

x8 = x1 + . . . + x7,

and let  = {x : x ∈ C}. Prove that C is a linear code. Prove that

is self-dual, i.e. that ^⊥= .

更多代写：全包网课化学  托福网考代考  商科quiz网课代考   美国essay写作  留学生论文作业  编程代做

合作平台：essay代写 论文代写 写手招聘 英国留学生代写