数学Final exam代考 mathematics代写

mathematics 220

Final Examination — December 20th 2016

数学Final exam代考 Candidates must follow any additional examination rules or directions communicated by the examiner(s) or invigilator(s).

This final exam has 8 questions on 12 pages, for a total of 100 marks.

Duration: 2 hours 30 minutes

Full Name (Last, First, All middle names):

Student-No: Course Section:

Signature:

Student Conduct during Examinations 数学Final exam代考

Each examination candidate must be prepared to produce, upon the request of the invigilator or examiner, his or her UBCcard for identifification.

Candidates are not permitted to ask questions of the examiners or invigilators, except in cases of supposed errors or ambiguities in examination questions, illegible or missing material, or the like.

No candidate shall be permitted to enter the examination room after the expiration of one-half hour from the scheduled starting time, or to leave during the fifirst half hour of the examination. Should the examination run forty-fifive (45) minutes or less, no candidate shall be permitted to enter the examination room once the examination has begun. 数学Final exam代考

Candidates must conduct themselves honestly and in accordance with established rules for a given examination, which will be articulated by the examiner or invigilator prior to the examination commencing. Should dishonest behaviour be observed by the examiner(s) or invigilator(s), pleas of accident or forgetfulness shall not be received.

Candidates suspected of any of the following, or any other similar practices, may be immediately dismissed from the examination by the examiner/invigilator,and may be subject to disciplinary action:

(a) speaking or communicating with other candidates, unless otherwise authorized;

(b) purposely exposing written papers to the view of other candidates or imaging devices;

(d) using or having visible at the place of writing any books, papers or other memory aid devices other than those authorized by the examiner(s); and,

(e) using or operating electronic devices including but not limited to telephones, calculators, computers, or similar devices other than those authorized by the examiner(s)–(electronic devices other than those authorized by the examiner(s) must be completely powered down if present at the place of writing). 数学Final exam代考

Candidates must not destroy or damage any examination material, must hand in all examination papers, and must not take any examination material from the examination room without permission of the examiner or invigilator.

Notwithstanding the above, for any mode of examination that does not fall into the traditional, paper-based method, examination candidates shall adhere to any special rules for conduct as established and articulated by the examiner.
Candidates must follow any additional examination rules or directions communicated by the examiner(s) or invigilator(s).

Question:	1	2	3	4	5	6	7	8	Total
Points:	32	10	10	10	8	10	10	10	100
Score:

Please read the following points carefully before starting to write. 数学Final exam代考

Readall the questions carefully before starting to work.
You should give complete arguments and explanations for all your answers and calcu- lations; answers without justifications will not be marked.
Continueon the back of the previous page if you run out of space.
Attemptto answer all questions for partial credit.

This is a closed-book examination. None of the following are allowed: documents,cheat sheets or electronic devices of any kind (including calculators, cell phones, etc.)

You may not leave during the first 30 minutes or final 15 minutes of the exam.

1.ForPart (a) to Part (g), determine whether the statements are true or false — Put True or False in the boxes. Part (h) is not a True/False type question. Justify your answers. 数学Final exam代考

(a)(4 marks) Let A, B be Then P(A ∪ B) ⊆ P(A) ∪P(B).

(b)(4 marks) Let R be a relation on the set A = {1, 2, 3} definedbelow

R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (1, 3), (3, 1)}.

Then R is an equivalence relation.

(c)(4marks)There is no smallest positive rational number.

(d)(4 marks) LetA_n = (0,¹ ) and B_n = (− 1 , 0) be open intervals for each n ∈ N. Then

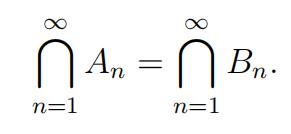
(e)(4marks) Let f, g, h be three functions from R to R. Then f ◦ (g + h) = f ◦ g + f ◦ h.

(f)(4 marks) Suppose n ∈ N, n ≥ 2, and [a], [b], [c] ∈ Z_nsuch that [c] ƒ= [0]. If [a] · [c] = [b] · [c], then [a] = [b]. 数学Final exam代考

(g)(4 marks) Let a, b, c ∈ R and c ≥ If ab < c, then a < √c or b <√c.

(h)(4marks) Let P, Q, R and S be Suppose that P is false and (R ⇒ S) ⇔(P ∧ Q) is true. Find the truth values of R and S.

2.Show for all integers n ≥ 0 that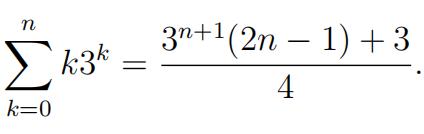

Prove: For all integers n we have 5 ‡ n²− 2.
Proveor disprove: for every a, n ∈ N with n ≥ 2, there exist distinct k, A ∈ N such that n divides a^k − a^A.
Let A, B, C be Prove: A × C ⊆ B × C if and only if A ⊆ B or C =∅.

6.Suppose that S ⊆ R is a set defined by 数学Final exam代考

S = {x ∈ R : x = m√π + n√2 for some m, n ∈ Z}

and S^j is a proper subset of S defined by

S^j = {x ∈ S : x = p√π + q√2 for some prime numbers p, q}.

(a)Show that S is countably infifinite.

(b)Is there a bijection from S^jto S? Justify your answer.

(If needed, you may use the fact that π, √2 are irrational numbers without proof.)

Let x ∈ R satisfy x⁷+ 5x² − 3 = 0. Prove that x is irrational. 数学Final exam代考

8.Let f : A → B be a function.Prove:

(a)(4 marks) If there is a function g: B A such that g f (x) = x, for all x A, then f is injective.

(b)(6marks) If f is injective, then there is a function g : B → A such that g ◦ f (x) = x, for all x ∈ A.

This page has been left blank for your workings and solutions.

合作平台：essay代写论文代写写手招聘英国留学生代写