Quiz 1
Math 317
数学exam代考 The fifirst 4 questions of this quiz can be served as a checklist for you to see how well you understand the concepts mentioned in this course.
Read before you start: The fifirst 4 questions of this quiz can be served as a checklist for you to see how well you understand the concepts mentioned in this course. The last 5 questions are more related to the contents after the midterm. I will give you plenty of time on this quiz and the only restriction is that you MUST do it on your own. Among this quiz,Q2 and Q3 are extremely fundamental so I will give them 1 extra bonus each to emphasize the importance. Also, those who answer Q9 (optional) correctly can get another bonus.
1.(6 × 4 marks) True or False. Justififications are required. 数学exam代考
(a)If˙r (s) is an arclength parameterization of the curve C, then its unit normal vector N˙ (s) is in parallel to the acceleration ˙r jj(s), i.e., 
.
(b)LetF˙ (x, y, z) be a vector field defined on D ⊂ R3. If ∇ × F= 0,then 
for all closed curve C ∈ R3.
(c)If a vector field F˙ (x, y, z) is continuously differentiable on a piecewise smooth surface S, S is given by G(x, y, z) = h(x, y) + z + 3 = 0, where h(x, y) is a continuously differentiable function, then the vectorial surface element of S can be defined as
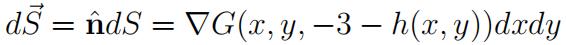
(d)Assume S is an outward oriented portion of the cylinder x2+ y2 = 1, 0 < z ≤ 3. If we add a downward disk S2 : z = 0, x2 + y2≤ 1, then for all F˙ continuously differentiable on R3,
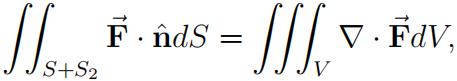
where V denotes the solid region enclosed by the cylinder x2 + y2 = 1 and the planes z = 0 and z = 3.
(e)AssumeS is a portion of the cone z = 
, z < 3. If we add a disk S2 : z = 3, x2 + y2 ≤ 9, and assume that both S and S2 are oriented upwarded, then for all F˙ continuously differentiable on R3,
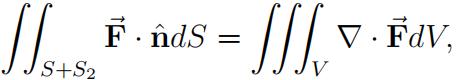
where V denotes the solid region enclosed by the cone z = x2 + y2 and the planes z = 3.
(f)Let F˙ = (x − y, y − z, x − z). If S1 and S2 are two smooth surfaces on R3 and ∂S1 = ∂S2, then
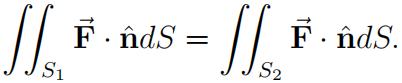
2.(8×3 marks + 1 bonus) Determine the types of the objects described below (empty set, point, curve, surface or solid region). 数学exam代考
For curves and surfaces, find one parameterization for each of them with the domain of your variables.
(a)Theintersection of the paraboloid z = x2 + 2y2 and the plane z = 2x.
(b)The intersection of the paraboloid z = x2+ 4y2 and the plane z = 2x −1.
(c)The object that is described as {<x, y, z> ∈ R3 : 2x + 3y + z = 5, x2+ y2 ≤ 4}.
(d)Theobject that is described as {<x, y, z> ∈ R3 : x2 + y2 ≤ 4, 0 ≤ z ≤ 2 − x}.
(e)The object that is described as {<x, y, z> ∈ R3 : z3= x2 + y2, 0 ≤ z ≤ 1}.
(f)Theboundary of the object described in (e).
(g)The object that is described as {<x, y, z> ∈ R3 : z4= 1 − x2 − y2}.
(h)Theboundary of the object described in (g).
3.(4×4 marks + 1 bonus)Find the vectorial surface element dS˙ = nˆdS for the following surfaces. 数学exam代考
(a)The plane ax + by + cz + d = 0, where a, b, c and d are constants and you may leave your answer in terms of them.
(b)The paraboloid given by x + z2+ y2 = −4.
(c)Theellipsoid 4x2 +4y2 +z2 = 4 lies in the region D : {(x, y, z) : x2 +z2 ≤ 1, y ≥ 0}.
(d)Thesurface defined by (z − 2)2 + z = −2x2 − xy + 3.
4.(23 marks)Determine whether the following functions are scalar functions or vectorial function.
For scalar ones, compute their gradient, and for vectorial ones, compute their divergence and curl.
(a)F(x, y, z) = x sin y + xz2 + 
.
(b)F(x, y, z) = <x sin y, xz2,
)>.
5.(8marks)Let S be a portion of the paraboloid z = 4 (x2 + y2) with restrictions
0 ≤ z ≤ 3, the vector field F˙ (x, y, z) =< y2 cos z, ex+z 1, x2z + y2z>. Find the outward flux Ψ through S, i.e.,
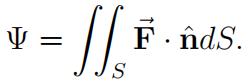
6.(8marks) Let S be the portion of the ellipsoid x2 + 4y2 + z2 = 4 where z ≥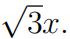 
数学exam代考
Suppose that S is oriented so that the unit normal vector at (0, 0, 2) is<0, 0, 1 >. Let F˙ be a vector field such that
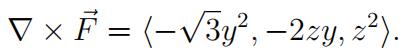
Use Stokes’s theorem to compute 
7.(6marks) Let F˙ (˙x) = A˙x, A =
, where aij are real constants.
(a)Findthe condition on A so that F˙has a scalar potential. 数学exam代考
(b)Findthe condition on A so that F˙has a vector potential.
8.(8 marks) The vector field F˙ = <x − y, y − z, x − 2z> has a vector poten. Find avector potential A˙ = (A1, A2, A3) with A3 = 0 (the answer may not be unique but you are just required to find one).
9.(1bonus) Let f, g be smooth scalar functions on R3 and F˙ be a smooth vector field on R3. Find the condition on ∇f and ∇g so that ∇×(g∇ f ) = ˙0. Specify vector identities that you are using, but you are not required to justify them.
