数学2302代写 Discrete Mathematics II代写

MATH2302 Discrete Mathematics II

数学2302代写 1.Recall that a binary string is a sequence of 0’s and 1’s.(a) How many binary strings of length 16 have at most three 1’s? (1 mark)

1.

Recall that a binary string is a sequence of 0’s and 1’s.

(a) How many binary strings of length 16 have at most three 1’s? (1 mark)

(b) Determine the number of binary strings of length 16 in which the pattern 100 occurs exactly four times. (3 marks)

 

2.  数学2302代写

Recall that µ : Z⁺  → {−1, 0, 1} is the Möbius function, see the reference pages for more details. Let

S = {2 ⁱ 3 ʲ  for 0 ≤ i, j ≤ 3} = {1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216}.

Defifine the poset (S, ρ) by a ρ b if and only if a|b and µ(a) = µ(b) for all integers a and b in S. You do not need to prove that (S, ρ) is a poset.

(a) List the minimal elements of this poset. (2 marks)

(b) List the maximal elements of this poset. (2 marks)

(c) Determine the length of a maximum chain in this poset, and justify your answer (4 marks)

 

3.  数学2302代写

Determine all the partitions of 50 into parts of consecutive sizes. (Note that in addition to listing the partitions, you need to justify that you have found all of them (4 marks)

 

 

5.  

Determine whether each of the following sequences is graphical; if the sequence is graphical, then draw a graph having that degree sequence, if the sequence is not graphical, then brieflfly explain why not. (4 marks)

(a) 5, 5, 4, 4, 4, 1, 1

(b) 6, 6, 6, 5, 5, 5, 4, 4, 4, 3, 3, 2, 2

 

6.  数学2302代写

Indicate whether each of the following statements is True or False. No explanation required. Recall that a graph does not have any loops or multiple edges. (6 marks)

(a) Up to isomorphism, the 6-cycle C₆ is the only 2-regular graph of order 6.

(b) A graph with 9 vertices and 6 edges has at least 3 components.

(c) The graph K_m,n is Hamiltonian if and only if m = n and m ≥ 2.

(d) There exists a 4-regular graph of order 10 that is not Hamiltonian.

(e) If the largest independent set in a graph of order 16 is 3, then the chromatic number of G is at least 6.

(f) The edge chromatic number of any graph is no larger than the order of the graph.

 

7.  数学2302代写

(a) Draw a 3-regular graph of order 18 that has no perfect matching. No explanation required. (3 marks)

 

(b) Find a minimum weight spanning tree in the weighted graph shown below. (3 marks)

 

 

 

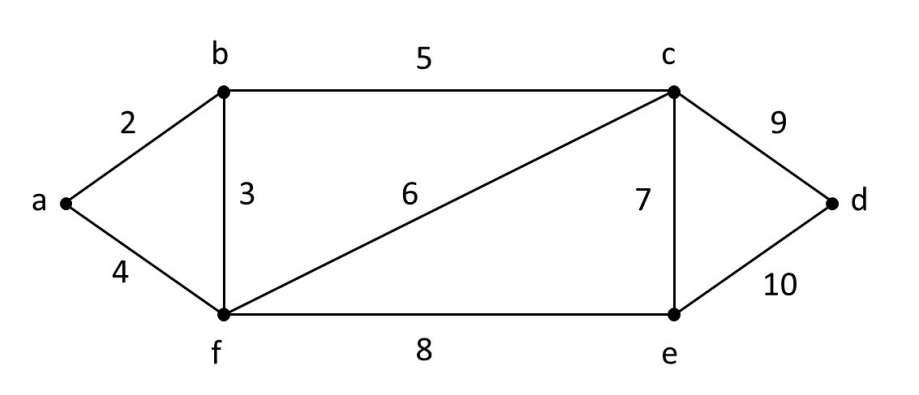
8.  

Find a minimum weight perfect matching in the weighted complete bipartite graph G with parts { v₁, v₂, v₃, v₄, v₅ } and{u₁, u₂, u₃, u₄, u₅}. The weight w(vᵢu_j ) of the edge vᵢu_j is given byw(vᵢu_j ) = mᵢ_j where M = [mᵢ_j ] is the matrix shown below. (5 marks)

 

 

9.  数学2302代写

Consider the word abcd﹣¹c﹣¹da﹣¹d﹣¹.

(a) Draw the polygon that is represented by this word. (1 mark)

(b) Compute the Euler characteristic of the corresponding surface. (2 marks)

(c) Is the corresponding surface orientable or non-orientable? (No explanation required.) (1 mark)

(d) Name the surface that this word represents. (1 mark)

 

10.  数学2302代写

Given any closed surface S, we can add a crosscap to S by cutting out a small disc and attaching a Möbius band to the resulting boundary, giving a new closed surface S‘.

 

 

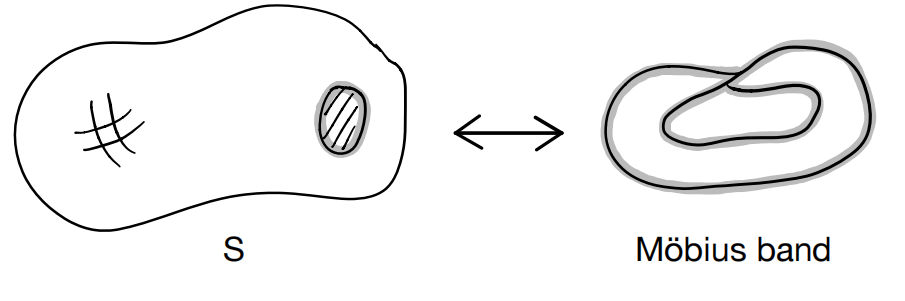
(a) Give a formula (with explanation) for χ(S’ ) in terms of χ(S). (3 marks)

(b) Determine whether S’ is orientable and explain your answer. Your answer is allowed to depend upon the orientability of S. (2 marks)

(c) What surface do we obtain when we add a crosscap to the torus? You should give your answer in terms of the classifification theorem (i.e., your answer should be a sphere, or a connected sum of k tori for some k, or a connected sum of ι projective planes for some ι). (1 mark)

 

11.  数学2302代写

(a) Determine the number of triples in a Steiner triple system of order 19. (2 marks)

(b)  A Steiner triple system of order 15 is constructed using the Bose Construction and contains the following four triples.

{(1, 1),(3, 1),(5, 2)}        {(4, 3),(2, 3),(5, 1)}       

{(4, 2),(1, 2),(2, 3)}        {(4, 1),(5, 1),(3, 2)}

Write down the triple containing the points (1, 3) and (3, 1). (4 marks)

 

12.

Does there exist a symmetric Latin square with symbol set {1, 2,…,n} for some integer n ≥ 3 such that there is exactly one occurrence of symbol 1 on the main diagonal, and exactly two occurrences of the symbol 2 on the main diagonal? Explain fully. (5 marks)

 

 

其他代写：作业代写 report代写 paper代写 code代写 algorithm代写 作业加急 北美代写 CS代写 Data Analysis代写 data代写 澳大利亚代写 essay代写 assignment代写 analysis代写 homework代写 加拿大代写 英国代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写