COMP9020 2019 Term 3
数学 Assignment代写 Submission is through WebCMS/give and should be a single pdf file, maximum size 2Mb. Prose should be typed, not handwritten.
Assignment 3
Due: Sunday, 24th November, 23:59
Submission is through WebCMS/give and should be a single pdf file, maximum size 2Mb. Prose should be typed, not handwritten. Use of LATEX is encouraged, but not required.数学 Assignment代写
Discussion of assignment material with others is permitted, but the work submitted must be your own in line with the University’s plagiarism policy.
Problem 1 (40 marks)数学 Assignment代写
For this question, let F denote the set of well-formed formulas over a set Prop of propositional variables.
(a)Showthat the logical equivalence relation, ≡, is an equivalence relation on F. (12 marks)
(b)List four elements in [⊥], the equivalence classof ⊥. (4 marks)
(c)For all ϕ, ϕj, ψ, ψj∈ F with ϕ ≡ ϕj and ψ ≡ ψj; show that:
(i)¬ϕ≡ ¬ϕj (4 marks)
(ii)ϕ∧ ψ ≡ ϕj ∧ ψj (4 marks)
(iii)ϕ∨ ψ ≡ ϕj ∨ ψj (4 marks)数学 Assignment代写
Let us define F≡ to be the set of equivalence classes of F under ≡. That is,
F≡ := {[ϕ] : ϕ ∈ F}.
Part (c) above shows that the following operations are well-defined1 on F≡:
- [ϕ]∧ [ψ] defined to be [ϕ ∧ ψ]
- [ϕ]∨ [ψ] defined to be [ϕ ∨ ψ]
- [ϕ]j defined to be[¬ϕ]
(d)Show that F≡together with the operations defined above forms a Boolean Algebra. Note: you will have to give a suitable definition of a zero element and a one element in F≡. (12 marks)
1well-defined means that the output is not dependent on different representations of the same input.
Problem 2 (10 marks)数学 Assignment代写
This is the Petersen graph:
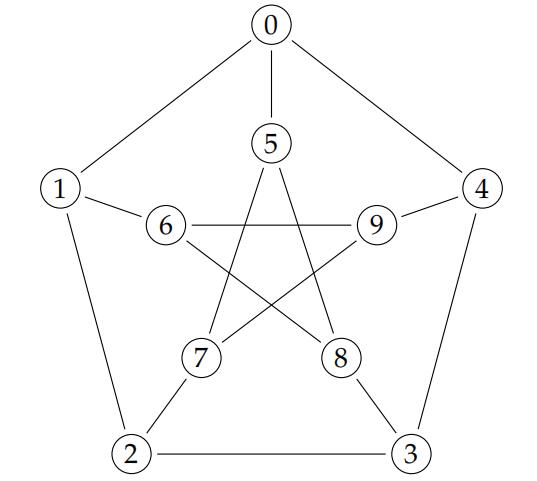
(a)Givean argument to show that the Petersen graph does not contain a subdivision of K5. (5 marks)
(b)Show that the Petersen graph contains a subdivisionof K3,3. (5 marks)
Problem 3 (10 marks)数学 Assignment代写
Harry would like to take each of the following subjects: Defence against the Dark Arts; Potions; Herbology; Transfiguration; and Charms. Unfortunately some of the classes clash, meaning Harry cannot take them both. The list of clashes are:
- Defenceagainst the Dark Arts clashes with Potions and Charms
- Potions also clashes withHerbology
- Herbology also clashes with Transfiguration,and
- Transfiguration also clashes with
Harry would like to know the maximum number of classes he can take.
(a)Model this as a graph problem. Rememberto:
(i)Clearlydefine the vertices and edges of your (4 marks)
(ii)State the associated graph problem that you need to (2 marks)
(b)Givethe solution to the graph problem corresponding to this scenario; and solve Harry’s (4 marks)
Problem 4 (22 marks)
Recall from Assignment 2 the definition of a binary tree data structure: either an empty tree, or a node with two children that are trees.数学 Assignment代写
Let T(n) denote the number of binary trees with n nodes. For example T(3) = 5 because there are five binary trees with three nodes:

(a)Using the recursive definition of a binary tree structure, or otherwise, derive a recurrence equationforT(n). (8 marks)
A full binary tree is a non-empty binary tree where every node has either two non-empty children (i.e. is a fully-internal node) or two empty children (i.e. is a leaf).
(b)Using observations from Assignment 2, or otherwise, explain why a full binary tree must have an odd numberof (4 marks)
(c)Let B(n) denote the number of full binary trees with n Derive an expression for B(n), involving of T(nj ) where nj ≤ n. Hint: Relate the internal nodes of a full binary treeto T(n). (6 marks)数学 Assignment代写
A well-formed formula is in Negated normal form if it consists of just , , and literals (i.e. propositional variables or negations of propositional variables). That is, a formula that results after two steps of the process for transforming a formula into a logically equivalent one. For example, p ∨ (¬q ∧ ¬r) is in negated normal form; but p ∨ ¬(q ∨ r) is not.
Let F(n) denote the number of well-formed, negated normal form formulas2 there are that use precisely n propositional variables exactly one time each. So F(1) = 2, F(2) = 16, and F(4) = 15360.
(d)Using your answer for part (c), give an expression for F(n). (4 marks)
2Note: we do not assume ∧ and ∨ are associative
Problem 5 (18 marks)
Consider the following graph:
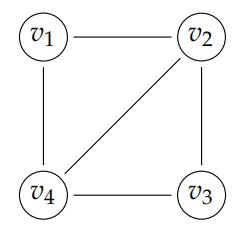
and consider the following process:
- Initially, start atv1.
- At each time step, choose one of the vertices adjacent to your current location uniformly at random, and move there.
Let p1(n), p2(n), p3(n), p4(n) be the probability your location after n time steps is v1, v2, v3, or v4 respectively. So p1(0) = 1 and p2(0) = p3(0) = p4(0) = 0.
(a)Expressp1(n + 1), p2(n + 1), p3(n + 1), and p4(n + 1) in terms of p1(n), p2(n), p3(n), and p4(n).(6 marks)数学 Assignment代写
(b)As n gets larger, each pi(n) converges to a single value (called the steady state) which can be deter- mined by setting pi(n + 1) = pi(n) in the above Determine the steady state probabilities forall vertices. (8 marks)
(c)The distance between any two vertices is the length of the shortest path between them. What is your expected distance from v1in the steady state? (4 marks)
Advice on how to do the assignment
All submitted work must be done individually without consulting someone else’s solutions in accordance with the University’s “Academic Dishonesty and Plagiarism” policies.
- Assignmentsare to be submitted via WebCMS (or give) as a single pdf
- Be careful with giving multiple or alternative answers. If you give multiple answers, then we will give you marks only for your worst answer, as this indicates how well you understood the question.数学 Assignment代写
- Some of the questions are very easy (with the help of the lecture notes or book). You can use the material presented in the lecture or book (without proving it). You do not need to write more than necessary (see comment above).
- When giving answers to questions, we always would like you to prove/explain/motivate your an- swers.
- If you use further resources (books, scientific papers, the internet,…) to formulate your answers, then add references to your sources.

其他代写:algorithm代写 analysis代写 app代写 assembly代写 C++代写 course代写 dataset代写 java代写 web代写 北美作业代写 编程代写 考试助攻 program代写 cs作业代写 source code代写 dataset代写 finance代写 data代写
