MF 796: Computational Methods in Mathematical Finance
数学金融作业代写 Option Pricing via FFT Techniques The Heston Model is defined by the following system of stochastic differential equations
Professors Christopher Kelliher and Eugene Sorets Spring 2019
Problem set # 3 数学金融作业代写
Due: Wednesday, February 13, by 8am
1.Option Pricing via FFT Techniques The Heston Model is defined by the following system of stochastic differentialequations:
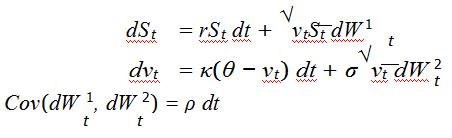
The characteristic function for the Heston Model is known to be: 数学金融作业代写
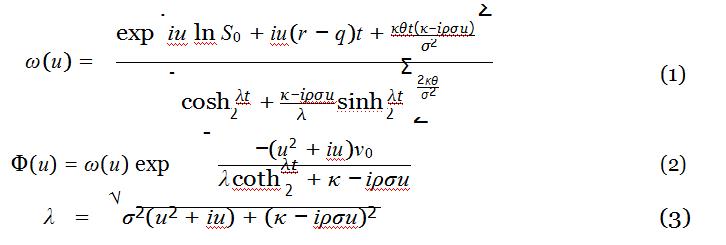
Assume the risk-free rate is 2%, the initial asset price is 250 and that the asset pays no dividends.
(a)Exploring FFT Technique Parameters Consider a European Call Option with strike 250 expiring in six month. 数学金融作业代写
Additionally, assume you know that the parameters of the Heston Model are:
| σ | = | 0.2 |
| ν0 | = 数学金融作业代写 | 0.08 |
| κ | = | 0.7 |
| ρ | = | −0.4 |
| θ | = | 0.1 |
i.Calculatethe price of the European Call option with many values for the damping factor, α. What values of α seem to lead to the most stable price?

ii.Using the results above, choose a reasonable value of α and calculate the price of the same European Call with various values of N and ∆k (or equivalently N and B). Comment on what values seem to lead to the most accurate prices, and the efficiency of each parameterization.数学金融作业代写
iii.Calculate the price of a European Call with strike 260 using various values of N and ∆k (or N and B). Do the same sets of values for N , B and ∆k produce the best results? Comment on any differences that arise.
(b)Exploring Heston Parameters Assume the risk-free rate is 2.5%, the initial asset priceis 150 and that the asset pays no dividends.数学金融作业代写
| σ | = | 0.4 |
| ν0 | = | 0.09 |
| κ | = | 0.5 数学金融作业代写 |
| ρ | = | 0.25 |
| θ | = | 0.12 |
i.Using these parameters, calculate Heston Model prices for three-month options at a range of strikes and extract the implied volatilities for each strike. Plot the impliedvolatility σ(K) as a function of strike.数学金融作业代写
ii.Usethe FFT pricing technique to obtain prices of 150 strike calls at many Extract the implied volatility for each and plot the term structure of volatility by plotting time to expiry on the x-axis and implied volatility on the y-axis.
iii.Holdingall other parameters constant, vary each of the model parameters and plot the updated volatility skews and term structures. Comment on the impact that each parameter has on the skew and term structure.

其他代写:代写CS C++代写 java代写 r代写 金融经济统计代写 matlab代写 web代写 app代写 作业代写 物理代写 数学代写 考试助攻 algorithm代写
