CSC 165 H1 — Question 1 of 4
数学表达与推理代写 1.[6 marks]For both statements below:(i)Write the negation of the original statement without using the ¬ symbol.
Submission Instructions
- You may type your answers or hand-write them legibly, on paper or using a tablet and stylus.
- You may write your answers directly on the question paper, or on another piece of paper/document.
- You may submit your answers as a single fifile/document or as multiple fifiles/documents. Each document may contain answers for only part of one question, an entire question, or multiple questions, but please label each part of your answers to make it clear what you are answering.
- You may name your fifile(s) any way you want (there is no “required fifile”).
- You must submit your answers in PDF or as photos (JPEG/JPG/GIF/PNG/HEIC/HEIF). Other for-mats (e.g., Word documents, LATEX source fifiles, ZIP fifiles) are NOT accepted—you must export or compile documents to PDF, convert images into a supported format, and upload each fifile individually. 数学表达与推理代写
For all questions in this test, “proof” means a formal proof that includes a header, and a proof body with justififications for each deduction. Each question can be answered correctly in less than one (1) page, and some questions have very short correct answers. You will NOT be penalized directly if you use more space for your answer, but longer answers increase the chance of errors… Remember that we are looking for evidence that you understand the conventions for writing correct proofs—NOT just how to answer these specifific questions—so pay close attention to the structure of your answers!
1.[6 marks] 数学表达与推理代写
For both statements below:
(i)Write the negation of the original statement without using the ¬ symbol.
(ii)Write whether the original statement is true or false.
(iii)If the original statement is true, prove it. If the original statement is false, disprove it.
(Note: The notation R≥0 represents the set [0, ∞) = {x ∈ R | x ≥ 0}.)
(a)∀x ∈ R, ∀n ∈ Z,(x < n) ⇒ (3x > 7n − 4)
(b)∀x ∈ R≥0, ∃n ∈ Z,(x ≤ n) ∧ (6 + 10x > 3n2 + 3)
Don’t forget: this test contains four separate questions (plus the Academic Integrity statement)!
2.[5 marks] 数学表达与推理代写
This question tests you on “proof by induction”. Even if there is a simple proof using another technique, you will receive at most half the marks if you do NOT use a proof by induction.
In your answer, you may use the facts that e = 2.71828 . . . and 1/e = 0.367879 . . . Also, if you want to look at the graph of any function in this question, you may use https://www.desmos.com/calculator—but NO other online resource is allowed.
Use induction to prove the following statement. As part of your answer, make sure to provide an explicit defifinition for your predicate P(n), and to state clearly what you are proving in each section of your proof.
∀n ∈ N,(n ≥ 2) ⇒ (e1-n + 3 < n2 + 2)
3.[3 marks] 数学表达与推理代写
This question tests you on “proof by contradiction”. Even if there is a simple proof using another technique, you will receive at most half the marks if you do NOT use a proof by contradiction.
Defifinition: A Pythagorian prime p is a prime number for which ∃d ∈ N, p = 4d + 1.
For example, 5 is a Pythagorean prime because 5 = 4(1) + 1.
Give a proof by contradiction that 11 is NOT a Pythagorean prime.
4. [5 marks]
In this question, you must use the following defifinition of absolute value:
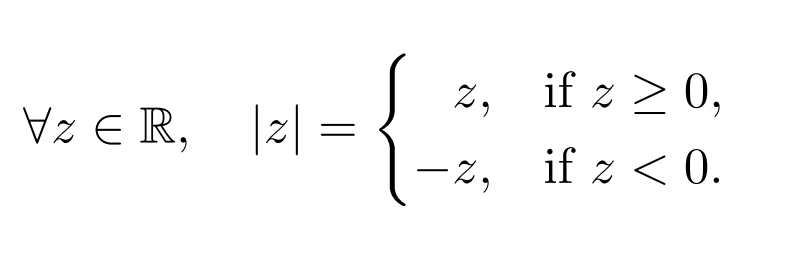
Prove that every solution to
|x − 6| ≤ b − 2x
belongs to the set (−∞, b − 6], where b is the last non-zero digit in your student number. (Here, “last” means furthest to the right; for example, if your student number is 1000305070, the last non-zero digit is “7”.)

其他代写: homework代写 北美作业代写 algorithm代写 analysis代写 app代写 assembly代写 C/C++代写 code代写 CS代写 cs作业代写 Data Analysis代写 essay代写 英国代写 Exercise代写 finance代写
