School of Mathematics and Statistics
MT4003 Groups
Problem Sheet VI: Finite Abelian Groups
数学网课代修价格 Deduce that if H is a subgroup of G, then H is a direct product of at most t cyclic groups of prime-power order.
1.List all the abelian groups of order 64 up to isomorphism. 数学网课代修价格
List all the abelian groups of order 2025 up to isomorphism.
2.List all the abelian groups of order 1000 up to isomorphism.
For the group G = C8 × C5 × C25, fifind the orders of elements and the number of elements of each order.
Do there exist two non-isomorphic abelian groups of order 1000 with the same number of elements of order 10?

3.Prove that a fifinite abelian group that is not cyclic contains a subgroup isomorphic to Cp × Cp for some prime p. 数学网课代修价格
Prove that no cyclic group contains such a subgroup.
4.Prove that, for every fifinite abelian group G and every divisor m of |G|, there is a subgroup of G of order m.
[Hint: First consider the case when G is cyclic of prime-power order.]
5.Let p be a prime and suppose that G is an abelian group of order a power of p. Write
![]()
as a direct product of cyclic groups of prime-power order.
Show that M = { x ∈ G | xp = 1 } is a subgroup of G and that
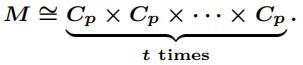
Deduce that if H is a subgroup of G, then H is a direct product of at most t cyclic groups of prime-power order.
6.Consider the group G = C3 × C9 × C85. Describe the subgroups of G up to isomorphism.
7.Consider the group G = C3 × C3. Determine the number of ordered pairs (x, y) such that {x, y} is a generating set for G. 数学网课代修价格
8.Consider the group G = C3 ×C3 × C27.
(a) Determine how many elements there are in G of order 3.
(b) Determine how many elements there are in G of order 9.
(c) Determine how many subgroups there are in G of order 3.
(d) Determine how many subgroups there are in G of order 9. [Hint: Use Question 7.]

更多代写:商业剖析代写 雅思indicator作弊 蒙特利尔网课代修 留学生Exam Essay代写 留学申请论文代写 Finite Mathematics代考
