数学编程代写 Python代写

Programming for Math and Science Project 2

数学编程代写 Goal: Implement substitution and elimination algorithms Purpose: Gain fine control of numerical linear algebra Logistics: The draft should be as

Goal: Implement substitution and elimination algorithms

Purpose: Gain fine control of numerical linear algebra

Logistics: The draft should be as polished as you can make it. 50% of the grade will come from the draft version, you will then receive feedback to improve it, and 50% of the grade will come from the final version.

Details: In the following, an m by n matrix is represented by a length-m list of lists. Always write down the steps of a concrete example by hand when developing your algorithm. It is the surest and fastest way to spot a bug. Also, print all indices to ensure they are taking the value you think they are.

Part 1. 数学编程代写

The first task is to write a function

def BackSub(U, b):
  """Solve the upper triangular system Ux = b by backward 
  substitution.
  """
  ...
  return x

and

def ForwSub(L, b):
  """Solve the upper triangular system Lx = b by forward substitution.
  """
  ...
  return x

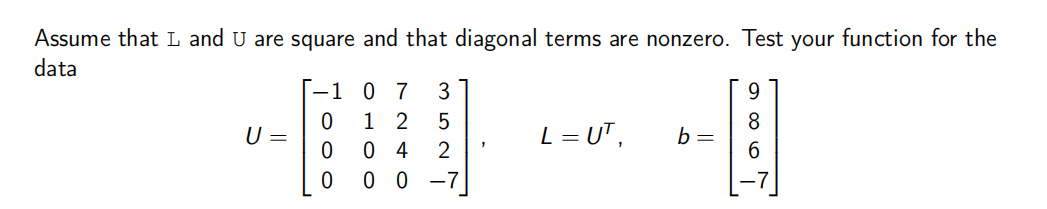
Part 2.

Now write a function

def GE0(A):
  """Performs Gaussian elimination on a square matrix with row exchanges. Return the lower triangular matrix L and upper triangular matrix U so that LU = A.
  """
  ...
  return L, U

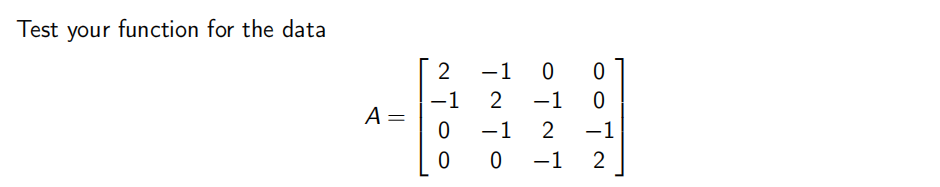
Part 3. 数学编程代写

A little more advanced, include partial pivoting (row exchanges). Write a function

def GE1(A):
  """Performs Gaussian elimination on a square matrix A with row   exchanges. Return the lower triangular matrix L, upper triangular matrix U, and permutation matrix P so that LU = PA.
  """
  ...
  return P, L, U

Recall that the row exchanges happen as follows: if eliminating column j, find the row i ≥ j with the largest value for |a_ij|, and swap it with the jth row.

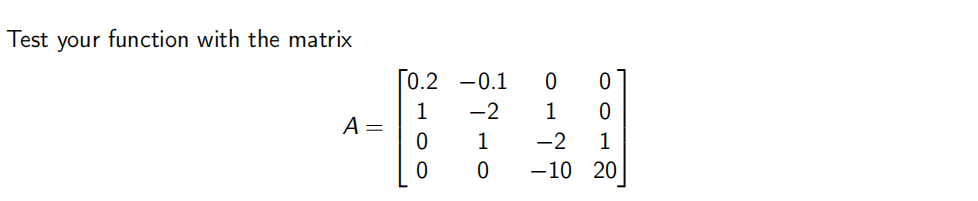
Part 4. 数学编程代写

Finally, combine part 1 and part 2 into one function

def Solve(A, RHS):
  """Solve the linear system Ax = RHS for an invertible square matrix A.
  """
  ...
  return x

The Solve function has three parts. First, it performs elimination on A to derive the factorization P A = LU: If Ax = RHS; then

LUx = P Ax = PRHS

Second, solve for Ux using forward substitution. Finally, solve for x using backward substitution. Check your results for the case RHS = [0.1, 0, 0, 10].

合作平台：essay代写论文代写写手招聘英国留学生代写

Programming for Math and Science Project 2

Part 1. 数学编程代写

Part 2.

Part 3. 数学编程代写

Part 4. 数学编程代写

关键字：