Math 223 Practice Midterm 2
数学线性代数代写 Instructions: This examination consists of 8 questions for a total of 122points. You have one hour and fifty minutes to complete thisexamination.
Instructions:
- This examination consists of 8 questions for a total of 122points.
- You have one hour and fifty minutes to complete thisexamination.
- No aids are permitted. Do not use books, notes, calculators,computers, tablets or phones.
- Write legibly and darkly.
- Cross out any work that you do not wish to have scored.
- Show all of your work. Unsupported answers may not earn credit.
1. 数学线性代数代写
Complete the following sentences with a mathematicallycorrect definition. No marks will be awarded for a “close” but incorrect definition.

(d) (2 points) The function T : Rn → Rm is a linear transformation if
(e) (2 points) The range of a linear transformation T : Rn → Rm is
(f) (2 points) The image of X ⊂ Rn under a linear transformation T : Rn → Rm is
(g) (2 points) The null space of a linear transformation T : Rn → Rm is
(h) (2 points) The n × n identity matrix is
(i) (2 points) The row space of a matrix M is
(j) (2 points) The dimension of a subspace V ⊆ Rn is
2. 数学线性代数代写
Let P ⊆ R4be the plane with equations x + y − z − w = 2 , x + y + z + w = 0 and let Q =
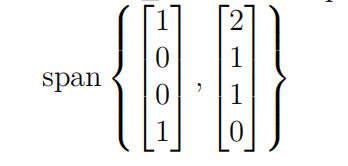
(a) (3 points) Is P a subspace? Prove your answer.
(b) (3 points) Is Q a subspace? Prove your answer.
(c) (3 points) Is P ∩ Q a subspace? Prove your answer.
(d) (3 points) Is P ∪ Q a subspace? Prove your answer.

3. 数学线性代数代写
For each of the following, give an example if possible.Otherwise, explain why it is impossible.
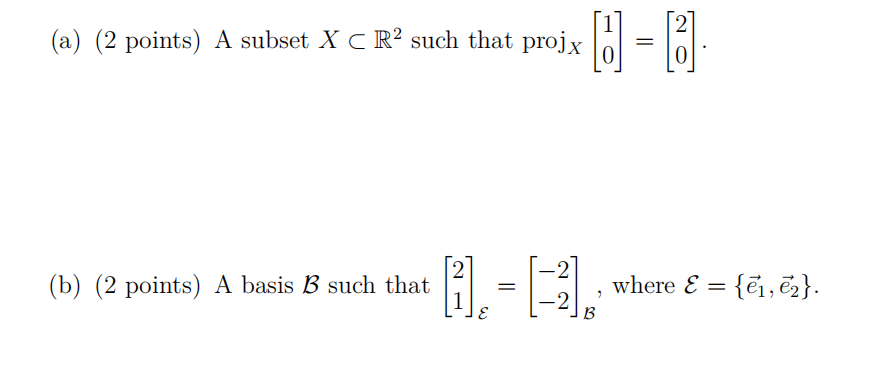
(c) (2 points) A 2 × 2 matrix whose null space equals its column space.
(d) (2 points) A 2 × 2 matrix whose null space equals its row space.
(e) (2 points) A 2 × 2 matrix whose row space equals its column space.

(g) (2 points) A linear transformation from T : R2 → R1 whose null space equals to its range.

(l) (2 points) 2 × 2 matrices A, B, C so that AB = BA but AC ≠ CA.
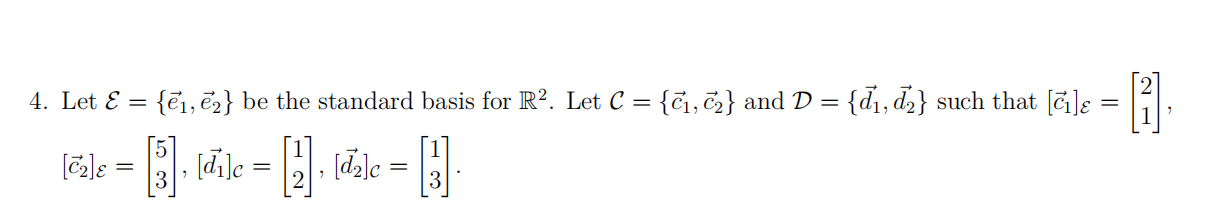
(a) (2 points) Is C a basis? Explain using the definition of basis.
(b) (2 points) Is D a basis? Explain using the definition of basis.





8.(7 points) 数学线性代数代写
On this question, you will be graded on yourcommunication as well as your correctness.
Note: part of good communication is writing in complete sentences, explaining what definitions you are using, having an argument that flows logically, and arranging your work neatly on the page.
Pat wants to find a linear transformation that will transform the figure on the left to the figure on the right.
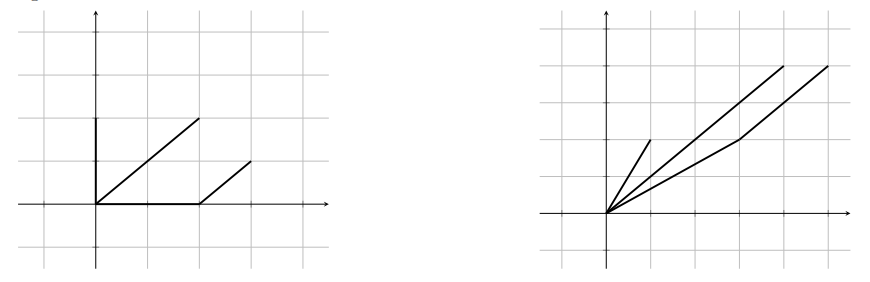
Either: (i) give Pat an example of such a transformation and explain how you found it or (ii) explain to Pat why no such linear transformation exists.

