MACM 401/MATH 801/CMPT 891
Assignment 5
数学算法代写 Question 1 Factorization in Zp[x] (20 marks) (a) Factor the following polynomials over Z11 using the Cantor-Zassenhaus algorithm.
Question 1
Factorization in Zp[x] (20 marks)
(a) Factor the following polynomials over Z11 using the Cantor-Zassenhaus algorithm.
a1= x4 + 8x2 + 6x + 8,
a2 = x6 + 3x5 − x4 + 2x3 − 3x + 3,
a3 = x8 + x7 + x6 + 2x4 + 5x3 + 2x2 + 8.
Use Maple to do all polynomial arithmetic, that is, you can use the Gcd(…) mod p and Powmod(…) mod p commands etc., but not Factor(…) mod p.
(b) Compute the square-roots of the integers a = 3, 5, 7 in the integers modulo p, if they exist, for p = 1020 + 129 = 100000000000000000129 by factoring the polynomial x2 − a in Zp[x] using the Cantor-Zassenhaus algorithm. Show your working. You will have to use Powmod here.
Question 2 数学算法代写
Factorization in Z[x] (25 marks)
Factor the following polynomials in Z[x].
a1 = x10− 6x4 + 3x2 + 13
a2 = 8x7 + 12x6 + 22x5 + 25x4 + 84x3 + 110x2 + 54x + 9
a3 = 9x7 + 6x6 − 12x5 + 14x4 + 15x3 + 2x2 − 3x + 14
a4 = x11 + 2x 10 + 3x9 − 10x8 − x7 − 2x6 + 16x4 + 26x3+ 4x2 + 51x − 170
For each polynomial, fifirst compute its square free factorization. You may use the Maple command gcd(…) to do this. Now factor each non-linear square-free factor as follows. Use the Maple command Factor(…) mod p to factor the square-free factors over Zp modulo the primes p = 13, 17, 19, 23. From this information, determine whether each polynomial is irreducible over Z or not. If not irreducible, try to discover what the irreducible factors are by considering combinations of the modular factors and Chinese remaindering (if necessary) and trial division over Z.
Using Chinese remaindering here is not effiffifficient in general. Why?
Thus for the polynomial a4, use Hensel lifting instead; using a prime of your choice from 13, 17, 19, 23, Hensel lift each factor mod p, then determine the irreducible factorization of a4 over Z.
Question 3
The linear x-adic Newton iteration (15 marks)

XadicSqrt := proc(a,x::name,p::prime)
# Input a(x) in Zp[x]
# Output sqrt(a) if it is in Zp[x] else FAIL
local a0,u0,u,i,k,d,m,e,uk;
if a=0 then return 0; fi;
d := degree(a,x);
if irem(d,2) <> 0 then return FAIL fi;
a0 := coeff(a,x,0);
if a0 = 0 then error “not implemented”; fi;
u0 := numtheory[msqrt](a0,p);
if u0 = FAIL then return FAIL; fi;
i := modp(1/2/u0,p);
u := u0;
e := Expand( a-u^2 ) mod p;
for k from 1 to d/2 do
uk := coeff(e,x,k)*i mod p;
u := u + uk*x^k;
e := Expand( a-u^2 ) mod p;
od;
if e = 0 then u else FAIL fi;
end:
The algorithm is correct but not effiffifficient. Let us fifind out why and then fifix it. 数学算法代写 Let deg a = d and let T(d) be the number of arithmetic operations algorithm XadicLift does in Zp. Assuming the polynomial multiplication u2 uses a classical quadratic algorithm, show that T(d) is cubic in d. You are to modify the computation of the error so that that T(d) ∈ O(d² ). You must show that T(d) ∈ O(d² ). Implement your modifified algorithm in Maple – just modify my code appropriately. Finally make your Maple code work for inputs where a0 = 0. Test your code on the following inputs for p = 11.
a = (9x³ + 3x² + 5x + 6)² , a = x³ + (9x³ + 3x² + 5x + 6)2 , a = (9x³ + 3x² + 5x)² .
Hint: The error ek+1 = a − (u(k+1)) ² = a − (u(k) + ukxk)² .
Use the error ek = a − u(k)2 from the previous iteration to calculate ek+1 faster.
Question 4 数学算法代写
Integration and Difffferentiation in Maple (10 marks)
(a) You were probably taught that the derivative of tan x is sec² x. Difffferentiate tan x in Maple. Now use Maple to show that Maple’s answer equals sec² x.
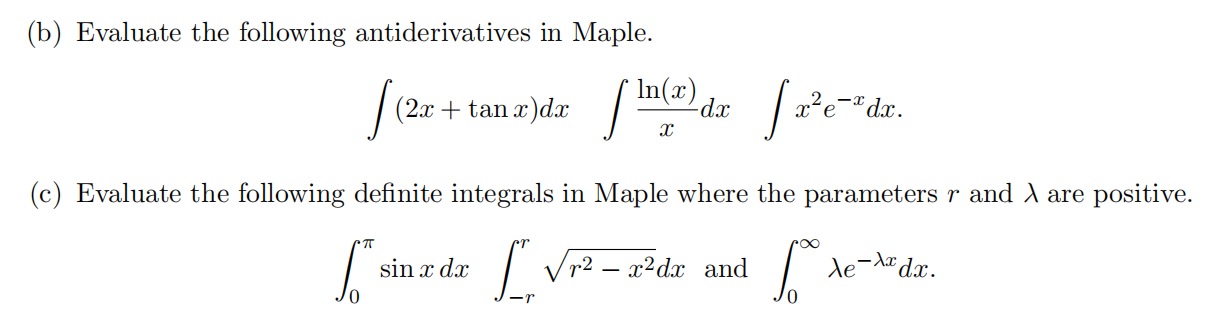
Question 5 数学算法代写
Symbolic Integration (15 marks)
Implement a Maple procedure INT (you may use Int if you prefer) that evaluates antiderivatives ∫f(x)dx. For a constant c and positive integer n your Maple procedure should apply
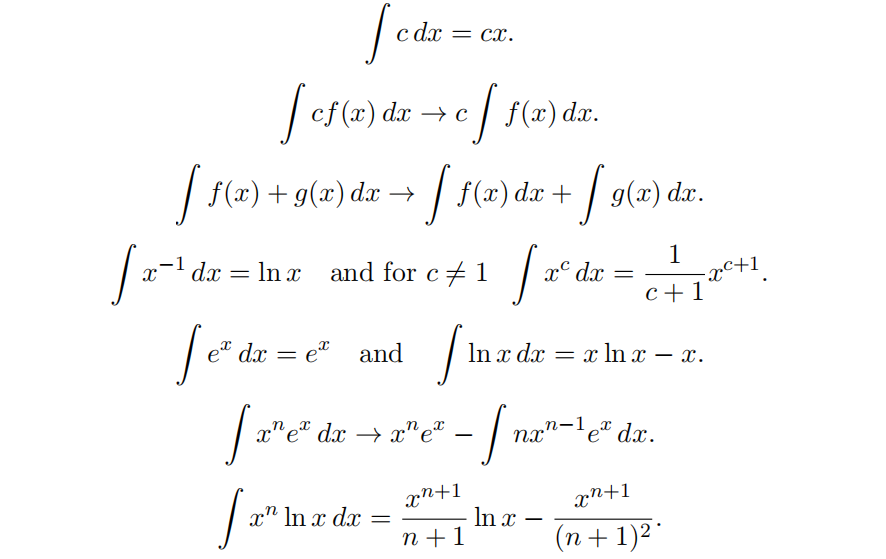
You may ignore the constant of integration. NOTE: ex in Maple is exp(x), i.e. it’s a function not a power. HINT: use the diff command for difffferentiation to determine if a Maple expression is a constant wrt x. Test your program on the following.
> INT( 2*f(x) + 3*y*x/2 + 3*ln(2), x );
> INT( x^2*exp(x) + 2*x*exp(x), x );
> INT( 4*x^3*ln(x), x );
> INT( 2*exp(-x) + ln(2*x+1), x );

其他代写:加拿大代写 作业代写 作业加急 北美代写 英国代写 北美作业代写 paper代写 assignment代写 homework代写 java代写 matlab代写 program代写 project代写 essay作业代写 finance代写 python代写 essay代写 report代写