IFYME004 Mathematics (Engineering) Examination Exemplar
数学工程代考 The line with equation y = x + 12 intersects the line withequation y = 2 − 4x at point P.Find the coordinates of point P. You must show your working.
INSTRUCTIONS TO STUDENTS 数学工程代考
Answer ALL questions
The marks for each question are indicated in square brackets [ ].
- A formula booklet and graph paper will be provided.
- An approved calculator may be used in the examination.
- Show ALL workings in your answer booklet.
- Examination materials must not be removed from the examination booklet.
DO NOT OPEN THIS QUESTION PAPER UNTIL INSTRUCTED BY THE INVIGILATOR
Question 1 数学工程代考
The table below shows the values of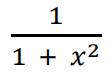 
for some values of x given to 3 significant figures where appropriate.
| x | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
| 1
1 + x2 |
1 |
0.962 |
0.862 |
0.735 |
0.610 |
0.5 |
Use the trapezium rule with five intervals to find an approximate value of
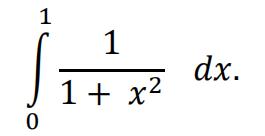
[ 3 ]
Question 2
a)The line with equation y = x + 12 intersects the line withequation y = 2 − 4x at point P.
Find the coordinates of point P. You must show your working. [ 3 ]
b)Point A lies at (2p, −q) and point B lies at (5p, 8q). A line which is perpendicular to AB has gradient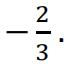 
Express p in terms of q. [ 3 ]
Question 3
a)A bag holds 8 red sweets, 4 blue sweets and 6 yellow sweets.
Three sweets are drawn, one after the other with no replacement.
Find the probability that all three sweets are red. Give your answer as a decimal to 3 significant figures.
In this question, 1 mark will be given for the correct use of significant figures.[ 4 ] 数学工程代考
b)The masses of melons can be assumed to follow a Normal distribution with standard deviation 40 grams.
A sample of 30 melons has a mean mass of 820 grams.
Find a 99% confidence interval for the mean mass of all the melons. [ 2 ]
Question 4 数学工程代考
A curve has equation y =3x3 + 7x2 − 28x − 32.
a)Use the Factor Theorem to show that (x + 4) is a factorof 3x3 + 7x2 − 28x − 32.[ 2 ]
(b)Divide 3×3 + 7x2− 28x − 32 by (x + 4) and hence factorise the expression completely. [ 3 ]
Question 5
a)In the expansion of(2 + cx)6, the coefficient of the x3 term is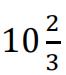 
times larger than the coefficient of the x4 term.
Find the value of c. [ 3 ] 数学工程代考
b)The 5th term of an arithmetic series is one more than the common difference.
If a is the first term and d is the common difference, show that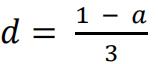 
and hence find an expression for the sum of the first 37 terms of the series,giving your answer in terms of a.[ 3 ]
(c)A geometric series has first term 240 and common ratio 
Show that the sum of the series cannot exceed 275. [ 2 ]
Question 6
a)
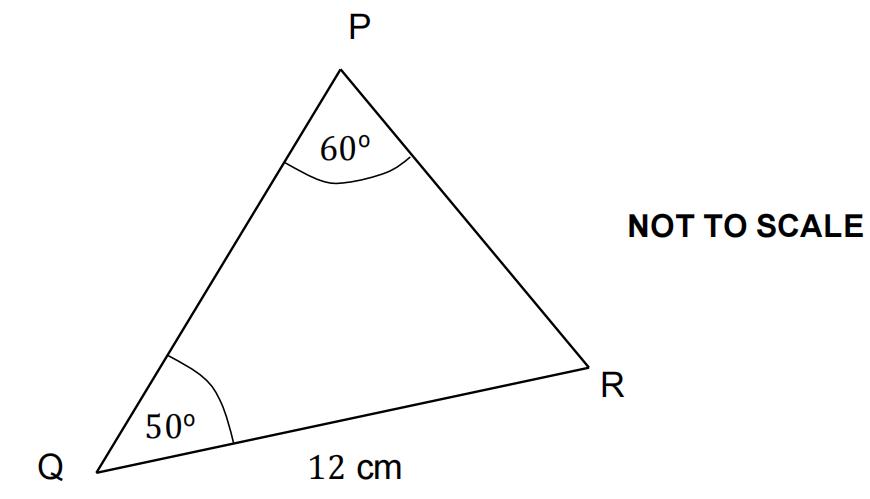
Figure 1
Figure 1 shows triangle PQR with angle P = 60o, angle Q = 50o and QR = 12 cm.
Find the length of PR and hence find the area of triangle PQR. [ 4 ]
b) Solve 2cos2θ=1 (0 ≤ 8 ≤ 2n)
Give your answers as exact multiples of π. [ 4 ]
Question 7 数学工程代考
Line l1 has equation r = (2i − j + 7k) + h(−i + 2j − 3k) where h is a scalar.
Line l2 has equation r = (i + 3j − 2k) + µ(2i − 5j + 9k) where µ is a scalar.
(a)Show that lines l1and l2 intersect and find the coordinates of their point of intersection.[ 6 ]
(b)Find the acute angle between lines l1and l2. [ 3 ]
You are given point P(4, −5, 13) lies on line l1 and point Q(3, −2, 7) lies on line l2.
(c)Find the unit vector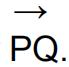 
[ 2 ]
Question 8
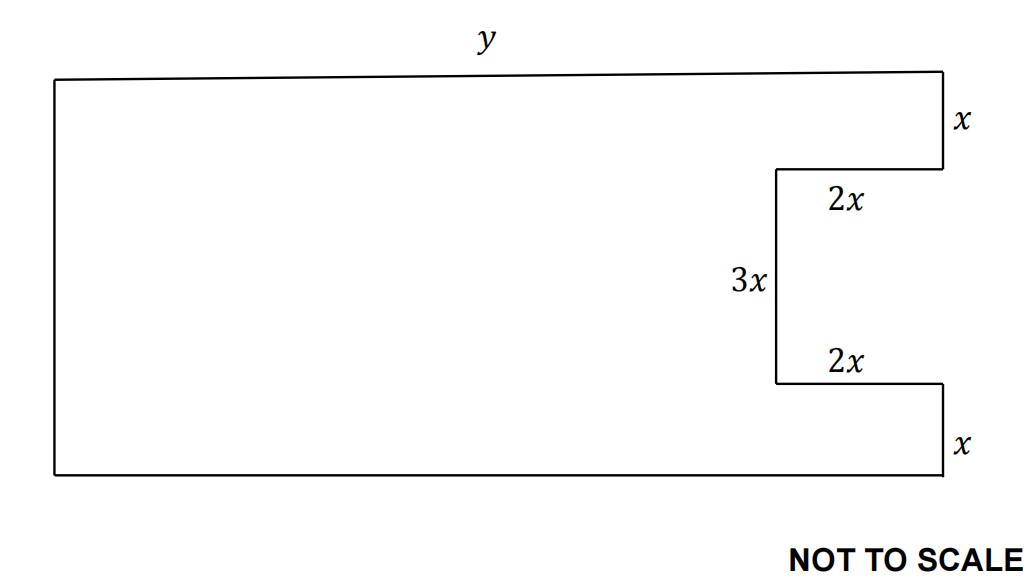
Figure 2
The shape in figure 2 shows a rectangular piece of wood with a smaller rectangle cut from one of the ends. All measurements are in cm.
The perimeter of the shape is 246 cm.
a)Express y in terms of x and hence show that the area of the shape, A, is given by
A = 615x − 41x2 [ 5 ]
(b)Use calculus to find the value of x which gives themaximum area. [ 3 ]
(c)Confirm that your value of x gives a maximum.[ 3 ]
Question 9
A circle has equation x2 + y2− 12x + 2y − 63 = 0.
a)Find the radius of the circle and the coordinates of its centre.[ 4 ]
b)Find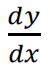
in terms of x and y. [ 3 ] 数学工程代考
(c)Confirm that point A(14, 5) lies on the circle and find the equation of the normal to the circle at point A.
Give your answer in the form ax + by + c = 0 where a, b and c are integers. [ 4 ]
Question 10
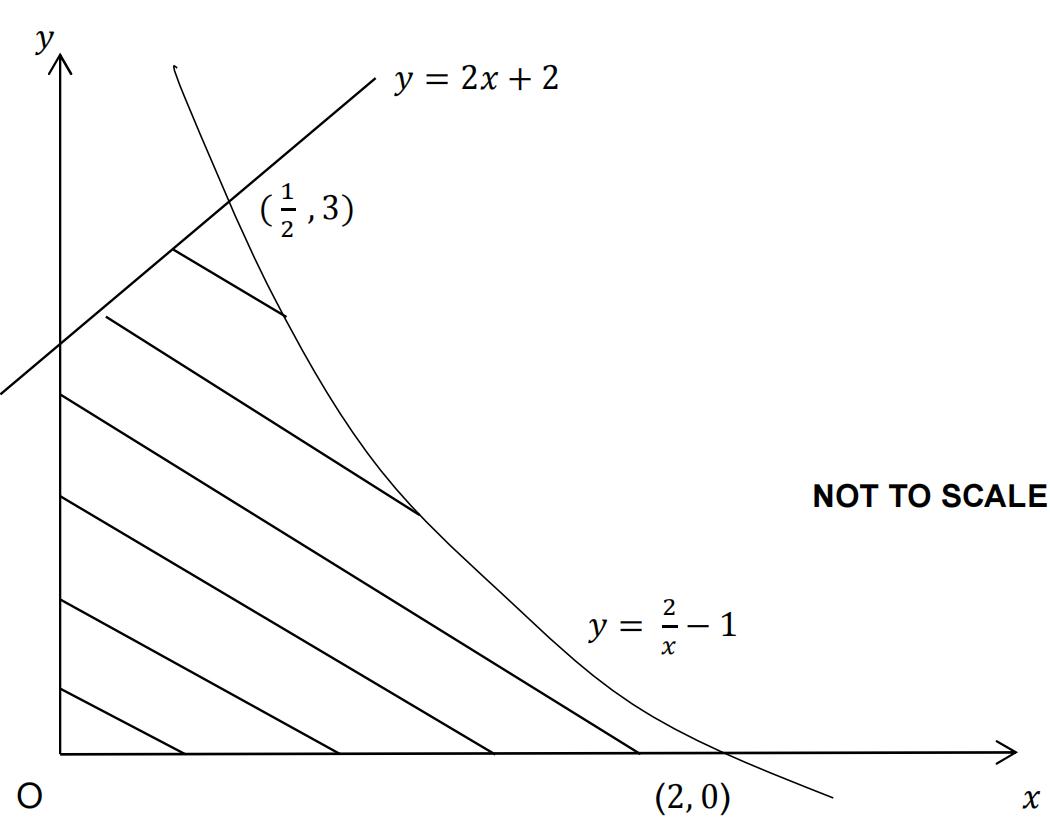
Figure 3
Figure 3 shows the curve y = 
− 1 and the line y = 2x + 2. The curve crosses the x− axis at (2, 0) and meets the line y = 2x + 2 at ( 
, 3).
Find the area, which is shaded on the diagram, that is bounded by the line
y = 2x + 2, the curve y = 
− 1 and both axes.
Give your answer in the form ln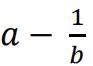 
where a and b are integers.[ 6 ]
All working must be shown. Just giving the answer, even the correct one, will score no marks if this working is not seen.
(b)Resolve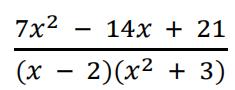 
into partial fractions. [ 4 ]
Question 11
a) Show that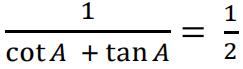 
sin 2A where A is acute. [ 3 ]
b) Solve 3 cos 2θ − cos θ + 1=0 (0 ≤ θ ≤ 360°) [ 5 ]
c) Differentiate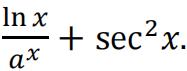 
Question 12 数学工程代考
Functions ƒ, g and ℎ are defined as follows:
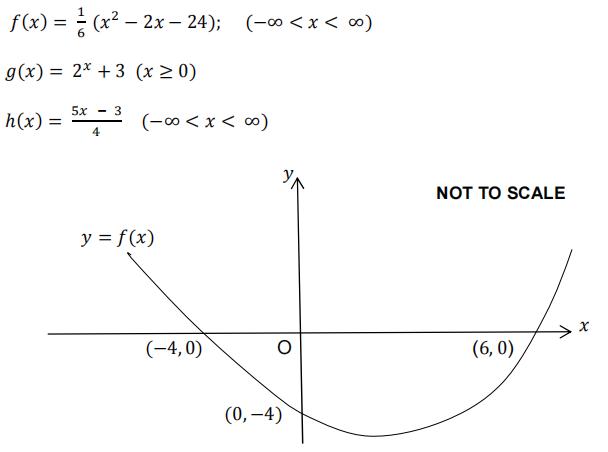
Figure 4
Figure 4 shows a sketch of y = ƒ(x). The curve crosses the x − axis at(−4, 0) and (6,0); and the y − axis at (0, −4).
a)Draw a sketch of y = ƒ(2x). This must not be drawn on graph paper. On your sketch, show clearly the coordinates where the graph crossesthe x − and y − axes.
Explain why y = ƒ(x) has no inverse. [ 4 ]
b)Find an expression for g–1(x). State its domainand [ 3 ]
c)Solve the equation ℎ[g(x)]= [ 3 ]
Question 13
a)Find the values of n if
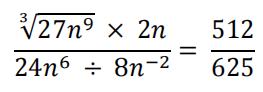
[ 3 ]
b)Solve the equation log5(5×3 + 3×2) − 3 log5x= 2 (x > 0)
All working must be shown.[ 4 ]
c)The variables p and t are connected by the formula p =e2t− 7et + 8t +1.
Find 
and hence find the exact value of t when 
= 2. [ 5 ]
Question 14
a)Evaluate
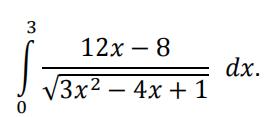
All working must be shown. Just giving the answer, even the correct one,will score no marks if this working is not seen. [ 5 ]
b)Find
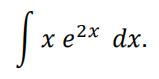
[ 3 ]
c)Solve the differential equation 数学工程代考
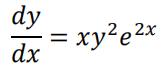
subject to y = 
when x = 0.
Give your answer in the form y = ƒ(x). [ 4 ]
