数学分析原理代写 Midterm代写

Midterm 1

数学分析原理代写 Throughout this exam, you may use any theorems from class, class assignments, or in the class textbook Chapters 1-8

Throughout this exam, you may use any theorems from class, class assignments, or in the class textbook Chapters 1-8, for which a proof has been provided.

Question 1: Uniform Convergence, Part I  数学分析原理代写

Consider the sequence of functions, {f_n}_n, for n ∈ N₊, given by:

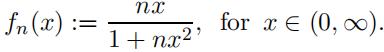
1. Findthe point-wise limit, f (x) = lim，
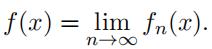
2. Prove that convergence to f (x) is notuniform over the interval (0, 1).
3. Prove the convergence to f (x) isuniform over the interval (1, ∞).

Question 2: Uniform Convergence, Part II  数学分析原理代写

Consider a function f : (0, ∞) → R, defined via the series:

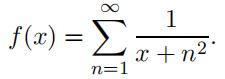
1. Considering the Riemann integral ” 1 f (x)dx, prove the following limitexists:

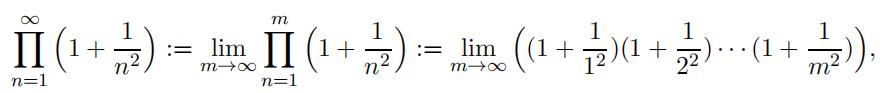
(Hint: Show e! 1 f (x)dx exists.)

2. Prove that  f (x)  is  differentiable.

Question 3: Stone – Weierstrass 数学分析原理代写

We denote by C([0, 1]), the space of real valued continuous functions with domain [0, 1] ⊂ R. We also give C([0, 1]) a metric space structure with the supremum norm:

d(f, g) := sup{|f (x) − g(x)| x ∈ [0, 1]}  for  f, g ∈ C([0, 1]).

Now consider the subset A ⊂ C([0, 1]):

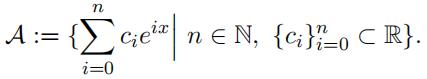
1. Prove that A is a dense subset ofC([0, 1]).
2. Assume f ∈ C([0, 1])satisfies:

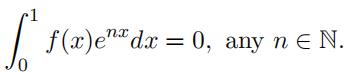
Prove f = 0.

更多代写：haskhell程序代写 haskhell程序代写 1000字-2000字的essay怎么写 article代写 Assignment论文写作  math数学代考

合作平台：essay代写 论文代写 写手招聘 英国留学生代写