CHAPTER 6
Mathematical Analysis代写 I built up my courage to ask her to dance By drinking too much before taking the chance. I fell on my butt when
Inferring a Binomial Probability via Exact Mathematical Analysis
Contents Mathematical Analysis代写
6.1.The Likelihood Function:Bernoulli Distribution 124
6.2.A Description of Credibilities: The BetaDistribution . 126
6.2.1Specifying abeta prior 127
6.3.ThePosterior Beta 132
6.3.1Posterior is compromise of priorand likelihood 133
6.4Examples 134
6.4.1Prior knowledge expressed as abeta distribution 134
6.4.2Prior knowledge that cannot be expressed as abeta distribution 136
6.5.Summary 138
6.6.Appendix: R Code forFigure 4 138
6.7.Exercises 139
I built up my courage to ask her to dance
By drinking too much before taking the chance. I fell on my butt when she said see ya later; Less priors might make my posterior beta.1Mathematical Analysis代写
This chapter presents an example of how to do Bayesian inference using pure analytical mathematics without any approximations. Ultimately, we will not use the pure analytical approach for complex applications, but this chapter is important for two reasons. First, the relatively simple mathematics in this chapter nicely reveal the underlying concepts of Bayesian inference on a continuous parameter. The simple formulas show how the continuous allocation of credibility changes systematically as data accumulate. The examples provide an important conceptual foundation for subsequent approximation methods, because the examples give you a clear sense of what is being approximated. Second, the distributions introduced in this chapter, especially the beta distribution, will be used repeatedly in subsequent chapters.
We continue with situations in which the observed datum has two nominal levels, and we would like to estimate the underlying probability of the two possible outcomes.
1 This chapter is about using the beta distribution as a prior distribution for the Bernoulli likelihood function, in which case the posterior distribution is also a beta distribution. The poem explains another way to make a posterior beta.
Doing Bayesian Data Analysis, 2nd Edition Copyright © 2015 Elsevier Inc. http://dx.doi.org/10.1016/B978-0-12-405888-0.00006-4 All rights reserved. 123
One stereotypical case is the flip of a coin,
in which the observed outcome could be heads or tails, and we want to estimate the underlying probabilities of the two outcomes.As has been emphasized before (e.g., Section 4.1.1, p. 73), the coin merely stands in for a real-world application we care about, such as estimating the success probability of a drug, or the probability correct on an exam, or the probability of a person being left handed, or the probability of successful free throw by a player in basketball,
or the probability that a baby is a girl, or the probability that a heart surgery patient will survive more than a year after surgery, or the probability that a person will agree with a statement on a survey, or the probability that a widget on an assembly line is faulty, and so on. While we talk about heads and tails for coins, keep in mind that the methods could be applied to many other interesting real-world situations.Mathematical Analysis代写
We require in this scenario that the space of possibilities for each datum has just two values that are mutually exclusive.
These two values have no ordinal or metric relationship with each other, they are just nominal values. Because there are two nominal values, we refer to this sort of data as “dichotomous,” or “nominal with two levels,” or “binomial.” We also assume that each observed datum is independent of the others. Typically, we will also assume that the underlying probability is stationary through time. Mathematical Analysis代写Coin flipping is the standard example of this situation: There are two possible outcomes (head or tail), and we assume that the flips are independent of each other and that the probability of getting a head is stationary through time.
In a Bayesian analysis, we begin with some prior allocation of credibility over possible probabilities of the coin coming up heads. Then, we observe some data that consist of a set of results from flipping the coin. Then, we infer the posterior distribution of credibility using Bayes’ rule. Bayes’ rule requires us to specify the likelihood function and that is the topic of the next section.
6.1. THE LIKELIHOOD FUNCTION: BERNOULLI DISTRIBUTION Mathematical Analysis代写
The Bernoulli distribution was defined back in Equation 5.10 (p. 109). We repeat it here for convenience. The outcome of a single flip is denoted y and can take on values of 0 or 1. The probability of each outcome is given by a function of parameter θ :
p(y|θ) = θy (1 − θ )(1−y) (6.1)
Notice that Equation 6.1 reduces to p(y 1 θ) θ , so the parameter θ can be interpreted as the underlying probability of heads for the coin flip. The formula in Equation 6.1 expresses the Bernoulli distribution, which is a probability distribution over the two discrete values of y, for any fixed value of θ . In particular, the sum of the
probabilities is 1, as must be true of a probability distribution: y p(y θ) p(y1 θ) p(y 0 θ) θ (1 θ) 1.Mathematical Analysis代写
Another perspective on Equation 6.1 is to think of the data value y as fixed by an observation,
and the value of θ as variable. Equation 6.1 then specifies the probability of the fixed y value as a function of candidate values of θ . Different values of θ yield different probabilities of the datum y. When thought of in this way, Equation 6.1 is the likelihood function of θ .
Notice that the likelihood function is a function of a continuous value θ , whereas the Bernoulli distribution is a discrete distribution over the two values of y. The likelihood function, although it specifies a probability at each value of θ , is not a probability distribution. In particular, it does not integrate to 1. For example, suppose we have observed that y = 1. Then, the integral of the likelihood function is ¸ 1 dθ θy(1 − θ )(1−y) = ¸ 1 dθθ = 1 , which does not equal 1.
In Bayesian inference, the function p(y θ) is usually thought of with the data, y,
known and fixed, and the parameter, θ , uncertain and variable. Therefore, p(y θ) is usually called the likelihood function for θ , and Equation 6.2 is called the Bernoulli likelihood function. Don’t forget, however, that the very same formula is also the probabilityof the datum, y, and can be called the Bernoulli distribution if θ is considered to be fixed and y is thought of as the variable.
We also previously figured out the formula for the probability of a set of outcomes, back in Equation 5.11 (p. 110), which again we repeat here for convenience. Denote the outcome of the ith flip as yi, and denote the set of outcomes as yi . We assume that the outcomes are independent of each other, which means that the probability of the set of outcomes is the multiplicative product of the probabilities of the individual outcomes. If we denote the number of heads as z y and the number of tails asN − z = .i(1 − yi), then
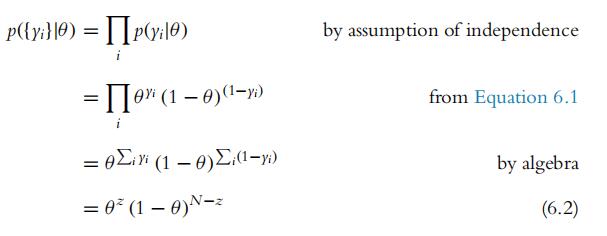
This formula is useful for applications of Bayes’ rule to large data sets. I will sometimeslapse terminologically sloppy and refer to the formula in Equation 6.2 as the Bernoullilikelihood function for a set of flips, but please remember that the Bernoulli likelihood function really refers to a single flip in Equation 6.1.2
6.2.A DESCRIPTION OF CREDIBILITIES: THE BETA DISTRIBUTION
In this chapter, we use purely mathematical analysis, with no numerical approximation,to derive the mathematical form of the posterior credibilities of parameter values. To dothis, we need a mathematical description of the prior allocation of credibilities. That is, we need a mathematical formula that describes the prior probability for each value of the parameter θ on the interval 0, 1 .Mathematical Analysis代写
In principle, we could use any probability density function supported on the interval 0, 1 . When we intend to apply Bayes’ rule (Equation 5.7, p. 106), however, there are two desiderata for mathematical tractability. First, it would be convenient if the productof p(y θ) and p(θ ), which is in the numerator of Bayes’ rule, results in a function of thesame form as p(θ ). When this is the case, the prior and posterior beliefs are describedusing the same form of function.
This quality allows us to include subsequent additional data and derive another posterior distribution,
again of the same form as the prior. Therefore, no matter how much data we include, we always get a posterior ofthesame functional form. Second, we desire the denominator of Bayes’ rule (Equation 5.9,p.107),namelydθ p(y θ )p(θ ), to be solvable analytically. This quality also depends onhow the form of the function p(θ ) relates to the form of the function p(y θ ). When theforms of p(y θ) and p(θ ) combine so that the posterior distribution has the same formas the prior distribution, then p(θ ) is called a conjugate prior for p(y θ ). Notice that the prior is conjugate only with respect to a particular likelihood function.
In the present situation, we are seeking a functional form for a prior density over θ that is conjugate to the Bernoulli likelihood function in Equation 6.1. If you think about it a minute, you’ll notice that if the prior is of the form θa(1 θ )b, then when you multiply the Bernoulli likelihood with the prior, you’ll again get a function of thesame form, namely θ(y+a)(1 − θ )(1−y+b). Therefore, to express the prior beliefs over θ , we seek a probability density function involving θa(1 − θ )b.
2Some readers might be familiar with the binomial distribution, p(z N, θ) N θz (1 θ)(N−z),
and wonder why it is not used here. The reason is that here we are considering each flip of the coin tobe a distinct event, whereby each observation has just two possible values, y 0, 1 . Therefore, the likelihood function is the Bernoulli distribution, which has two possible outcome values. The probability of the set of events is then the product of the individual event probabilities, as in Equation 6.2.Mathematical Analysis代写
If we instead considered a single “event” to be the flipping of N coins, then an observation of a single event could have N 1 possible values, namely z 0, 1, … , N . Then we would need a likelihood function that provided the probabilities of those N 1 possible outcomes, given the fixed value N that defines a single observational event. In this case, the probabilities of the values would be given by the binomial distribution. The binomial distribution is explained in the section accompanying Equation 11.5 on p. 303.
A probability density of that form is called a beta distribution.
Formally, a beta distribution has two parameters, called a and b, and the density itself is defined as
p(θ |a, b) = beta(θ |a, b)
= θ(a−1) (1 − θ )(b−1)/B(a, b) (6.3)
where B(a, b) is simply a normalizing constant that ensures that the area under the beta density integrates to 1.0, as all probability density functions must. In other words, the normalizer for the beta distribution is the beta function
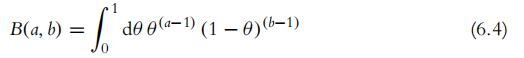
Remember that the beta distribution (Equation 6.3) is only defined for values of θ in the interval 0, 1 , and the values of a and b must be positive. Notice also that in the definition of the beta distribution (Equation 6.3), the value of θ is raised to the power a 1, not the power a, and the value of (1 θ) is raised to the power b 1, not the power b.
Be careful to distinguish the beta function,
B(a, b) in Equation 6.4, from the beta distribution, beta(θ a, b) in Equation 6.3. The beta function is not a function of θ because θ has been “integrated out,” the function only involves the variables a and b. In the programming language R, beta(θ a, b) is dbeta(θ ,a,b), and B(a, b) is beta(a,b).3
Examples of the beta distribution are displayed in Figure 6.1. Each panel of Figure 6.1plots p(θ a, b) as a function of θ for particular values of a and b, as indicated inside eachpanel. Notice that as a gets bigger (left to right across columns of Figure 6.1), the bulkof the distribution moves rightward over higher values of θ , but as b gets bigger (top tobottom across rows of Figure 6.1), the bulk of the distribution moves leftward over lowervalues of θ .Mathematical Analysis代写
Notice that as a and b get bigger together, the beta distribution gets narrower.The variables a and b are called the shape parameters of the beta distribution because they determine its shape, as can be seen in Figure 6.1. Although Figure 6.1 features mostly integer values of a and b, the shape parameters can have any positive real value.
6.2.1. Specifying a beta prior Mathematical Analysis代写
We would like to specify a beta distribution that describes our prior beliefs about θ . Youcan think of a and b in the prior as if they were previously observed data, in which there
3 Whereas it is true that B(a, b) 1 dθ θ(a−1) (1 θ)(b−1), the beta function can also be expressed as B(a, b) T(a)T(b)/ T(a b), where T is the Gamma function: T(a) 0∞ dt t(a−1) exp( t). The Gamma function is a generalization of the factorial function, because, for integer valued a, T(a) (a 1) . In R,T(a) is gamma(a). Many sources define the beta function this way, in terms of the Gamma function. We will not be using the Gamma function.
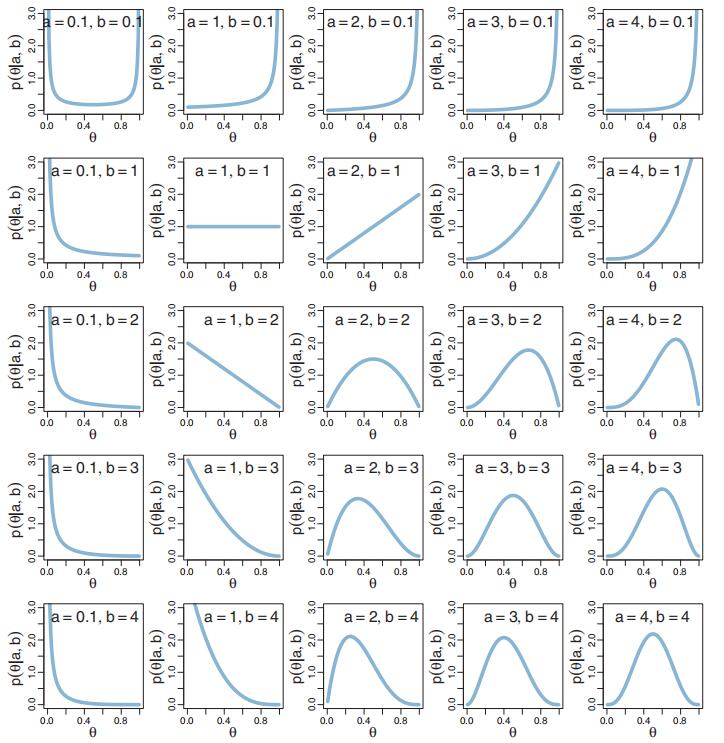
Figure 6.1 Examples of the beta distribution (Equation 6.1). The shape parameter a increases from leftto right across the columns, while the shape parameter b increases from top to bottom across the rows.
were a heads and b tails in a total of n a b flips.
For example, if we have no prior knowledge other than the knowledge that the coin has a head side and a tail side, that’s tantamount to having previously observed one head and one tail, which corresponds to a 1 and b 1. You can see in Figure 6.1 that when a 1 and b 1, the beta distribution is uniform: All values of θ are equally probable. As another example, if wethink that the coin is probably fair but we’re not very sure, then we can imagine that the previously observed data had, say, a 4 heads and b 4 tails. You can see in Figure 6.1 that when a 4 and b 4, the beta distribution is peaked at θ 0.5, but higher or lower values of θ are moderately probable too.Mathematical Analysis代写
Often we think of our prior beliefs in terms of a central tendency and certainty about that central tendency. For example, in thinking about the probability of left handedness in the general population of people, we might think from everyday experience that it’s around 10%. But if we are not very certain about that value, we might consider the equivalent previous sample size to be small, say, n 10, which means that of 10 previously observed people, 1 of them was left handed.
As another example,
in thinking about the probability that a government-minted coin comes up heads, we might believe that it is very nearly 50%, and because we are fairly certain, we could set the equivalent previous sample size to, say, n 200, which means that of 200previously observed flips, 100 were heads. Our goal is to convert a prior belief expressedin terms of central tendency and sample size into equivalent values of a and b in the beta distribution.
Toward this goal, it is useful to know the central tendency and spread of the beta distribution expressed in terms of a and b. It turns out that the mean of the beta(θ a, b) distribution is μ a/(a b) and the mode is ω (a 1)/(a b 2) for a > 1 and b > 1 (μ is Greek letter mu and ω is Greek letter omega).
Thus, when a b, the mean and mode are 0.5. When a > b,
the mean and mode are greater than 0.5, and when a < b, the mean and mode are less than 0.5. The spread of the beta distribution is related to the “concentration” κ a b (κ is Greek letter kappa). You can see from Figure 6.1 that as κ a b gets larger, the beta distribution gets narrower or more concentrated.Solving those equations for a and b yields the following formulas for a and b in terms of the mean μ, the mode ω, and the concentration κ:
a = μκ and b = (1 − μ)κ (6.5)
a = ω(κ − 2) + 1 and b = (1 − ω)(κ − 2) + 1 for κ > 2 (6.6)
The value we choose for the prior κ can be thought of this way: It is the number of new flips of the coin that we would need to make us teeter between the new data and the prior belief about μ. If we would only need a few new flips to sway our beliefs, thenour prior beliefs should be represented by a small κ.Mathematical Analysis代写
If we would need a large numberof new flips to sway us away from our prior beliefs about μ, then our prior beliefs are worth a very large κ. For example, suppose that I think the coin is fair, so μ 0.5, but I’m not highly confident about it, so maybe I imagine I’ve seen only κ 8 previous flips. Then, a μκ 4 and b (1 μ)κ 4, which, as we saw before, is a beta distribution peaked at θ 0.5 and with higher or lower values less probable.
The mode can be more intuitive than the mean,
especially for skewed distributions, because the mode is where the distribution reaches its tallest height, which is easy tovisualize. The mean in a skewed distribution is somewhere away from the mode, in the direction of the longer tail. For example, suppose we want to create a beta distribution that has its mode at ω 0.80, with a concentration corresponding to κ 12.
Then, using Equation 6.6, we find that the corresponding shape parameters are a 9 and b 3. The lower panels of Figure 6.2 show plots of beta distributions for which the mode falls at θ 0.8. On the other hand, if we create a beta distribution that has its mean at 0.8, we get the distributions shown in the upper panels of Figure 6.2, where it can be seen that the modes are considerably to the right of the mean, not at θ 0.8.Mathematical Analysis代写
Yet another way of establishing the shape parameters is by starting with the mean and standard deviation, σ , of the desired beta distribution. You must be careful with this approach, because the standard deviation must make sense in the context of a betadensity. In particular, the standard deviation should typically be less than 0.28867, which
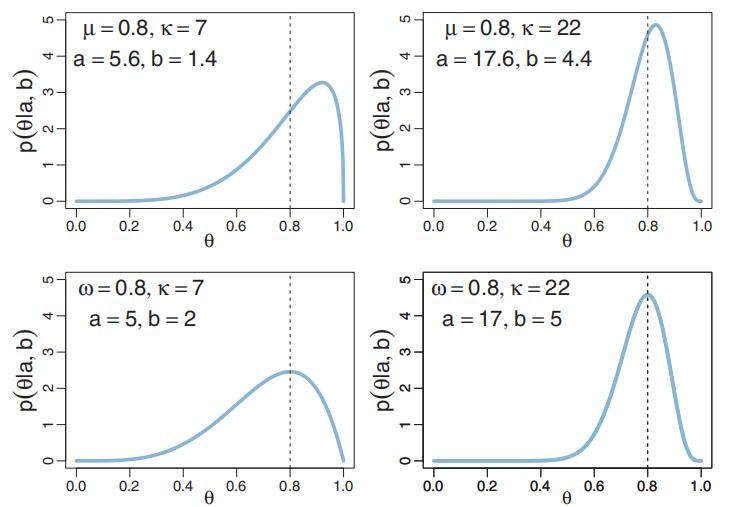
Figure 6.2 Beta distributions with a mean of μ 0.8 in the upper panels and a mode of ω 0.8 in the lowerpanels. Because the beta distribution is usually skewed, it can be more intuitive to think in terms of its mode instead of its mean. When κ is smaller, as in the left column, the beta distribution is wider than when κ is larger, as in the right column.
is the standard deviation of a uniform distribution.4 For a beta density with mean μ and standard deviation σ , the shape parameters are
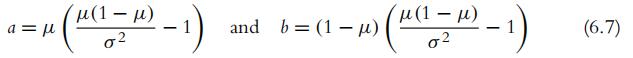
For example, if μ 0.5 and σ 0.28867, Equation 6.7 implies that a 1 and b 1. As another example, if μ 0.5 and σ 0.1, then a 12 and b 12, which is to say that a beta(θ 12, 12) distribution has a standard deviation of 0.1.
I have created convenient utility functions in R that implement the parameter transformations in Equations 6.5–6.7. The functions are loaded into R by typing source(“DBDA2E-utilities.R”), when that file is in the current working directory.
Hopefully, the function names are selfexplanatory, and here is an example of their use:
> betaABfromMeanKappa( mean=0.25 , kappa=4 ) $a [1] 1 $b [1] 3 > betaABfromModeKappa( mode=0.25 , kappa=4 ) $a [1] 1.5 $b [1] 2.5 > betaABfromMeanSD( mean=0.5 , sd=0.1 ) $a [1] 12 $b [1] 12
The functions return a list of named components. Therefore, if you assign the result of the function to a variable, you can get at the individual parameters by their component names,
as in the following example:
> betaParam = betaABfromModeKappa( mode=0.25 , kappa=4 ) > betaParam$a [1] 1.5 > betaParam$b [1] 2.5
In most applications, we will deal with beta distributions for which a ≥ 1 and
b ≥ 1, that is, κ > 2. This reflects prior knowledge that the coin has a head side and a
4 The standard deviation of the beta distribution is √μ(1 μ)/(a b 1). Notice that the standard deviation gets smaller when the concentration κ a b gets larger. While this fact is nice to know, we will not have use for it in our applications.Mathematical Analysis代写
tail side. In these situations when we know κ > 2, it can be most intuitive to use the parameterization of the beta distribution in terms of the mode in Equation 6.6. There are some situations, however, in which it may be convenient to use beta distributions in which a < 1 and/or b < 1, or for which we cannot be confident that κ > 2. For example, we might believe that the coin is a trick coin that nearly always comes up heads or nearly always comes up tails, but we don’t know which. In these situations, we cannot use the parameterization in terms of the mode, which requires κ > 2, and instead we can use the parameterization of the beta distribution in terms of the mean in Equations 6.5.

6.3. THE POSTERIOR BETA
Now that we have determined a convenient prior for the Bernoulli likelihood function, let’s figure out exactly what the posterior distribution is when we apply Bayes’ rule (Equation 5.7, p. 106). Suppose we have a set of data comprising N flips with z heads. Substituting the Bernoulli likelihood (Equation 6.2) and the beta prior distribution (Equation 6.3) into Bayes’ rule yields
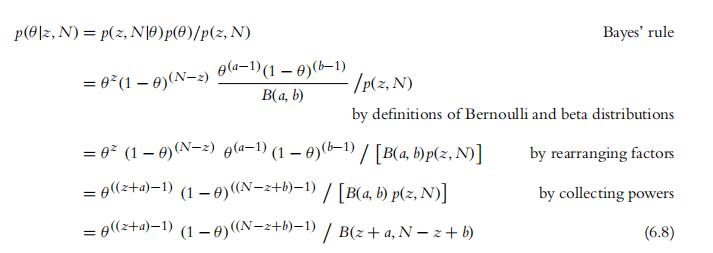
The last step in the above derivation, from B(a, b)p(z, N) to B(z a, N z b), was not made via some elaborate covert analysis of integrals. Instead, the transition was made simply by thinking about what the normalizing factor for the numeratormust be. The numerator is θ((z+a)−1) (1 θ )((N−z+b)−1), which is the numerator of a beta(θ z a, N z b) distribution. For the function in Equation 6.8 to be a probability distribution, as it must be, the denominator must be the normalizing factor for the corresponding beta distribution, which is B(z a, N z b) by definition of the beta function.5Mathematical Analysis代写
Equation 6.8 tells us a key point: If the prior distribution is beta(θ |a, b), and the data have z heads in N flips, then the posterior distribution is beta(θ |z + a, N − z + b).
5 As an aside, because B(a, b) p(z, N) = B(z + a, N − z + b), we re-arrange to find that p(z, N) =B(z + a, N − z + b)/B(a, b), which will be useful in Section 10.2.1.
The simplicity of this updating formula is one of the beauties of the mathematical approach to Bayesian inference. You can think about this updating formula with reference to Figure 6.1. Suppose the prior is beta(θ 1, 1), as shown in the second row and second column of Figure 6.1. We flip the coin once and observe heads. The posterior distribution is then beta(θ 2, 1), as shown in the second row and third columnof Figure 6.1. Suppose we flip the coin again and observe tails. The posterior distributionis now updated to beta(θ 2, 2), as shown in the third row and third column of Figure 6.1.This process continues for any amount of data. If the initial prior is a beta distribution, then the posterior distribution is always a beta distribution.
6.3.1.Posterior is compromise of prior and likelihood Mathematical Analysis代写
The posterior distribution is always a compromise between the prior distribution andthe likelihood function. The previous chapter (specifically Section 5.3) gave examples byusing grid approximation, but now we can illustrate the compromise with a mathematical formula. For a prior distribution expressed as beta(θ a, b), the prior mean of θ is a/(a b). Suppose we observe z heads in N flips, which is a proportion of z/N heads in the data. The posterior mean is (z a)/ (z a) (N z b)(z a)/(N a b). It turns out that the posterior mean can be algebraically re-arranged into a weighted average of the prior mean, a/(a b), and the data proportion, z/N , as follows:
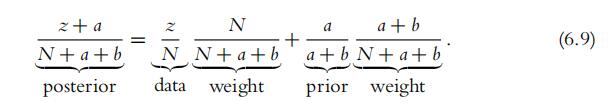
Equation 6.9 indicates that the posterior mean is always somewhere between the prior mean and the proportion in the data. The mixing weight on the data proportion increases as N increases. Thus, the more data we have, the less is the influence of the prior, and the posterior mean gets closer to the proportion in the data. In particular, when N a b, the mixing weights are 0.5, which indicates that the prior mean and the data proportion have equal influence in the posterior. This result echoes what was said earlier (Equation 6.5) regarding how to set a and b to represent our prior beliefs: The choice of prior n (which equals a b) should represent the size of the new data set that would sway us away from our prior toward the data proportion.Mathematical Analysis代写
Figure 6.3 illustrates an example of Equation 6.9.
The prior has a 5 and b 5, hence a prior mean of a/(a b) 0.5, and the data show z 1 with N 10, hence a proportion of heads of z/N 0.1. The weight on the prior mean is (a b)/ (N a b) 0.5, as is the weight on the data proportion. Hence, the mean of the posterior should be 0.5 0.5 0.5 0.1 0.3, which indeed it is, as shown inFigure 6.3.
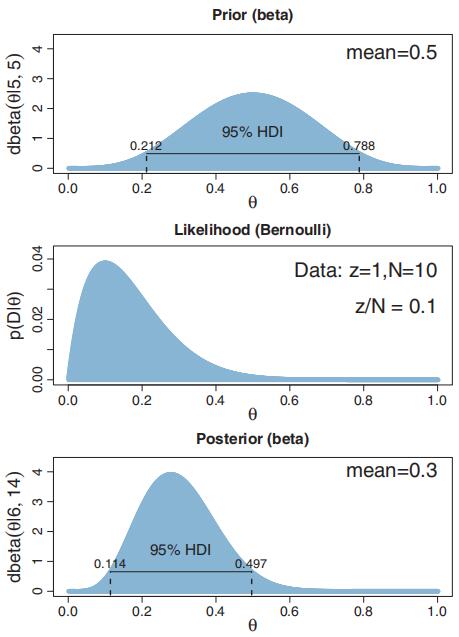
Figure 6.3 An illustration of Equation 6.9, showing that the mean of the posterior is a weighted combination of the mean of the prior and the proportion of heads in the data.
6.4. EXAMPLES Mathematical Analysis代写
6.4.1. Prior knowledge expressed as a beta distribution
Suppose someone has a coin that we know to be a regular, unaltered coin freshly mintedby a federal government. The person flips (or spins) the coin 20 times and it happens to come up heads 17 times, that is, 85% heads. What do you believe to be the underlying probability of heads for the coin? Despite the result from the 20 flips, the strong prior knowledge about the coin suggests that the result was a fluke and that the underlying probability of heads is, nevertheless, around 0.5.
The left column of Figure 6.4 illustratesthis reasoning. The top-left panel shows a beta prior distribution that expresses strongprior knowledge that the coin is fair. The prior uses a mode of ω = 0.5 and an effectiveprior sample size of κ 500, which translates into beta shape parameters of a 250 and b 250 using Equation 6.6. Scanning down to the lower-left panel, you can see that the posterior beta distribution is still loaded heavily over θ 0.5. It would take a lot more data to budge us away from the strong prior.Mathematical Analysis代写
Consider a different situation,
in which we are trying to estimate the probability that a particular professional basketball player will successfully make free throws. Suppose that all we know about the player is that he is in the professional league. Suppose we also know that professional players tend to make about 75% of their free throws, with mostplayers making at least 50% but at most about 90%.
This prior knowledge is expressed in the upper-middle panel of Figure 6.4, which used a beta distribution with mode ω 0.75 and equivalent prior sample of κ 25, so that the width of the 95% HDI of the prior captures our prior knowledge about the range of abilities in the professional league. Suppose we observe 20 free throws of the player, who successfully makes 17 of the attempts. This 85% success rate in the sample is impressive, but is this our best estimate of the player’s ability? If we appropriately take into account the fact that mostprofessional players only make about 75%, our estimate of this particular player’s ability is tempered. The posterior distribution in the lower-middle panel of Figure 6.4 shows a mode just under 80%.Mathematical Analysis代写
Finally, suppose we study a newly discovered substance on a distant planet,
using a remotely controlled robot. We notice that the substance can be blue or green, and we would like to estimate the underlying probability of these two forms. The robot takes 20 random samples and finds that 17 are blue. The right column of Figure 6.4 shows
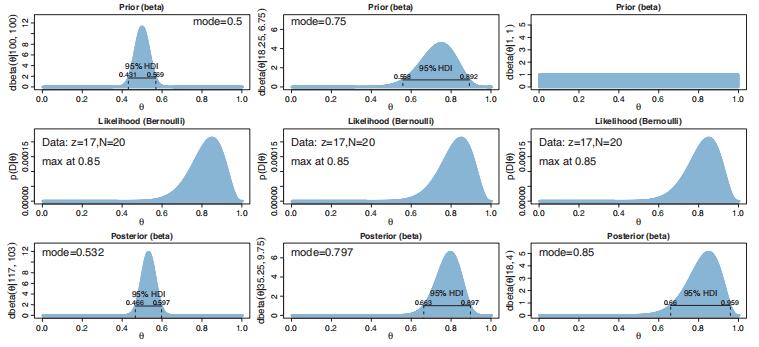
Figure 6.4 Examples of updating a beta prior distribution. The three columns show the same data with different priors. R code for this figure is described in Section 6.6.
the estimate of this probability, starting with a prior that uses only the knowledge that two colors exist. In this case, the mode of the posterior distribution is at 85%.
6.4.2.Prior knowledge that cannot be expressed as a beta distribution
The beauty of using a beta distribution to express prior knowledge is that the posteriordistribution is again exactly a beta distribution, and therefore, no matter how muchdata we include, we always have an exact representation of the posterior distribution and a simple way of computing it. But not all prior knowledge can be expressed by a beta distribution, because the beta distribution can only be in the forms illustrated by Figure 6.1. If the prior knowledge cannot be expressed as a beta distribution, then we must use a different method to derive the posterior. In particular, we might revert to grid approximation as was explained in Section 5.5 (p. 116). I provide an example here to illustrate the limits of using a beta prior.Mathematical Analysis代写
Suppose that we are estimating the underlying probability that a coin comes up heads,
but we know that this coin was manufactured by the Acme Magic and Novelty Company, which produces coins of two types: Some have probability of heads near 25%, and others have probability of heads near 75%. In other words, our prior knowledge indicates a bimodal prior distribution over θ , with peaks over θ 0.25 and θ 0.75. Unfortunately, there is no beta distribution that has this form.
We can instead try to express the prior knowledge as a grid of discrete values over θ . In this case, there is no uniquely correct way to do this, because the prior knowledge is not expressed in any specific mathematical form. But we can improvise.
Forexample, we might express the prior as two triangular peaks centered over 0.25 and 0.75, like this:
Theta = seq(0,1, length=1000 ) # Fine teeth for Theta. # Two triangular peaks on a small non-zero floor: pTheta = c( rep(1,200),seq(1,100,length=50),seq(100,1,length=50), rep(1,200) , rep(1,200),seq(1,100,length=50),seq(100,1,length=50), rep(1,200) ) pTheta = pTheta/sum(pTheta) # Make pTheta sum to 1.0
The expression above for pTheta is specifying the relative height of p(θ ) at each grid point in Theta. Because Theta has 1,000 components, we need pTheta to have 1,000 components. The first part of pTheta is rep(1,200), which says to repeat the height 1 a total of 200 times. Thus, the first 200 components of pTheta are a flat floor. The next part of pTheta is an incline: seq(1,100,length=50) goes from a height of 1 to a height of 100 in 50 steps. Then, the next part is a decline in 50 steps: seq(100,1,length=50). This gets us back to the floor, and the process repeats. The resulting prior can be seen in the top panel of Figure 6.5.Mathematical Analysis代写
Now suppose we flip the coin and observe 13 tails and 14 heads. We can enter the data and compute the posterior distribution using these commands:
Data = c(rep(0,13),rep(1,14)) posterior = BernGrid( Theta, pTheta , Data , plotType="Bars" , showCentTend="None" , showHDI=FALSE , showpD=FALSE )
(Don’t forget you must source BernGrid.R before using it.) The results are shown in Figure 6.5. Notice that the posterior has three bumps, which clearly could not be described by a beta distribution. The three bumps are a compromise between the two peaks of the prior and the middle peak of the likelihood. In this case, it seems that the prior and the data conflict: The prior says the coin should be biased away from θ 0.5,but the data suggest that the coin might be fair. If we collected a lot more data, the
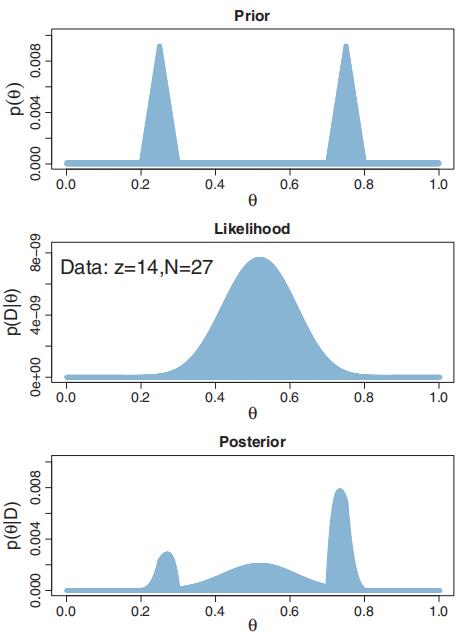
Figure 6.5 An example for which the prior distribution cannot be expressed by a beta distribution.
posterior would eventually overwhelm the prior, regardless of whether or not the prior was consistent with the data.
6.5. SUMMARY
The main point of this chapter was to demonstrate how Bayesian inference works when Bayes’ rule can be solved analytically, using mathematics alone, without numerical approximation. More specifically, this chapter illustrated a case in which the likelihood has a conjugate prior distribution, whereby the posterior distribution has the same math- ematical form as the prior distribution. This situation is especially convenient because we have a simple and exact mathematical description of the posterior distribution, no matter what data are included.Mathematical Analysis代写
Unfortunately, there are two severe limitations with this approach.
First, only simple likelihood functions have conjugate priors. In realistic applications that we encounter later, the complex models have no conjugate priors, and the posterior distributions have no simple form. Second, even if a conjugate prior exists, not all prior knowledge can be expressed in the mathematical form of the conjugate prior. Thus, although it is interesting and educational to see how Bayes’ rule can be solved analytically, we will have to abandon exact mathematical solutions when doing complex applications. We will instead use Markov chain Monte Carlo (MCMC) methods.Mathematical Analysis代写
This chapter also introduced you to the beta distribution, which we will continue to use frequently throughout the remainder of the book. Thus, despite the fact that we will not be using analytical mathematics to solve Bayes’ rule, we will be using the beta distribution to express prior knowledge in complex models.
6.6. APPENDIX: R CODE FOR FIGURE 6.4
The program BernBeta.R defines a function BernBeta for producing graphs like thosein Figure 6.4. The function behaves much like the function BernGrid that was explained in Section 5.5 (p. 116). Here is an example of how to use BernBetaExample.R. Youmust have R’s working directory set to the folder that contains the files BernBeta.R and DBDA2E-utilities.R.Mathematical Analysis代写
source(“DBDA2E-utilities.R”) # Load definitions of graphics functions etc. source(“BernBeta.R”) # Load the definition of the BernBeta function # Specify the prior:
t = 0.75 # Specify the prior mode. n = 25 # Specify the effective prior sample size. a = t*(n-2) + 1 # Convert to beta shape parameter a. b = (1-t)*(n-2) + 1 # Convert to beta shape parameter b. Prior = c(a,b) # Specify Prior as vector with the two shape parameters. # Specify the data: N = 20 # The total number of flips. z = 17 # The number of heads. Data = c(rep(0,N-z),rep(1,z)) # Convert N and z into vector of 0’s and 1’s. openGraph(width=5,height=7) posterior = BernBeta( priorBetaAB=Prior, Data=Data , plotType="Bars" , showCentTend="Mode" , showHDI=TRUE , showpD=FALSE ) saveGraph(file="BernBetaExample",type="jpg")
The first two lines above use the source function to read in R commands from files. The source function was explained in Section 3.7.2.
The next section of code, above, specifies the prior. The function BernBeta assumes that the prior is a beta distribution, and the function requires the user to provide the betashape parameters, a and b, as a vector for the argument priorBetaAB, in a form like this: BernBeta( priorBetaAB=c(a,b) , …). Because it can sometimes be unintuitive to think directly in terms of a and b, the code above instead starts by specifying the mode t and effective prior sample size n, and then converts to the equivalent a and b shape parameters by implementing Equation 6.6.Mathematical Analysis代写
The next section of code, above, specifies the data. The function BernBeta needs the data to be specified as a vector of 0’s and 1’s. The example instead begins by specifying the number of flips and the number of heads, and then uses the rep function to create a corresponding data vector.
The BernBeta function itself is called near the end of the script above.
The user must specify the arguments priorBetaAB and Data, but there are also several optional arguments. They behave much like the corresponding arguments in function BernGrid explained in Section 5.5 (p. 116). In particular, you might want to try showCentTend=”Mean”, which displays the means of the distributions instead of the modes.
If you want to specify the prior in terms of its mean instead of its mode, then you must implement Equation 6.5:
# Specify the prior: m = 0.75 # Specify the prior mean. n = 25 # Specify the effective prior sample size. a = m*n # Convert to beta shape parameter a. b = (1-m)*n # Convert to beta shape parameter b. Prior = c(a,b) # Specify Prior as vector with the two shape parameters.
The output of BernBeta, other than a graphical display, is the vector of a and b shape parameters for the posterior.Mathematical Analysis代写
6.7. EXERCISES
Look for more exercises at https://sites.google.com/site/doingbayesiandataanalysis/
Exercise 6.1.[Purpose: For you to see the influence of the prior in each successive flip, and for you to see another demonstration that the posterioris invariant under re-orderings of the data.]
For this exercise, use the R function explained in Section 6.6 (BernBeta.R). (Don’t forget to source the function before calling it.) Notice that the function returns the posterior beta values each time it iscalled, so you can use the returned values as the prior values for the next function call.
(A)Start with a prior distribution that expresses some uncertainty that a coin is fair: beta(θ 4, 4). Flip the coin once; suppose we get a head. What is the posterior distribution?
(B)Use the posterior from the previous flip as the prior for the next Suppose we flip again and get a head. Now what is the new posterior? (Hint: If you type post = BernBeta( c(4,4) , c(1) ) for the first part, then you can type post = BernBeta( post , c(1) )for the next part.)
(C)Usingthat posterior as the prior for the next flip, flip a third time and get a Now what is the new posterior? (Hint: Type post = BernBeta( post , c(0) ).)
(D)Do the same three updates but in the order T, H, H instead of H, H, Is the final posterior distribution the same for both orderings of the flipresults?
Exercise 6.2. [Purpose: Connecting HDIs to the real world, with iterative data collection.]
Suppose an election is approaching, and you are interested in knowing whether the general population prefers candidate A or candidate B. There is a just- published poll in the newspaper, which states that of 100 randomly sampled people, 58 preferred candidate A and the remainder preferred candidate B.Mathematical Analysis代写
(A)Suppose that before the newspaper poll, your prior belief was a uniform distribution.What is the 95% HDI on yourbeliefs after learning of the newspaper poll results?
(B)You want to conduct a follow-up poll to narrow down your estimate of the population’s In your follow-up poll, you randomly sample 100 other people and find that 57 prefer candidate A and the remainder prefer candidate B. Assuming that peoples’ opinions have not changed between polls, what is the 95% HDI on the posterior?
Exercise 6.3. [Purpose: Apply the Bayesian method to real data analysis. These data are representative of real data (Kruschke, 2009).]
Suppose you train people in a simple learning experiment, as follows. When people see the two words, “radio” and“ocean,” on the computer screen, they should press the F key on the computer keyboard. They see several repetitions and learn the response well. Then you introduce anothercorrespondence for them to learn: Whenever the words “radio” and “mountain” appear,they should press the J key on the computer keyboard. You keep training them until they know both correspondences well. Now you probe what they’ve learned by asking them about two novel test items. For the first test, you show them the word “radio” by itself and instruct them to make the best response (F or J) based on what they learned before.
For the second test, you show them the two words “ocean” and “mountain” and ask them to make the best response. You do this procedure with 50 people. Your data show that for “radio” by itself, 40 people chose F and 10 chose J. For the word combination “ocean” and “mountain,” 15 chose F and 35 chose J. Are people biased toward F or toward J for either of the two probe types? To answer this question, assume a uniform prior, and use a 95% HDI to decide which biases can be declared to be credible. (Consult Chapter 12 for how to declare a parameter value to be not credible.)
Exercise 6.4. [Purpose: To explore an unusual prior and learn about the beta distribution in the process.]
Suppose we have a coin that we know comes from a magic-trick store, and therefore we believe that the coin is strongly biased either usually to come up heads or usually to come up tails, but we don’t know which. Express this belief as a beta prior. (Hint: See Figure 6.1, upper-left panel.) Now we flip the coin 5 times and it comes up heads in 4 of the 5 flips. What is the posterior distribution? (Use the R function of Section 6.6 (BernBeta.R) to see graphs of the prior and posterior.)Mathematical Analysis代写
Exercise 6.5. [Purpose: To get hands on experience with the goal of predictingthe next datum, and to see how the prior influences that prediction.]
(A)Suppose you have a coin that you know is minted by the government and has not been tampered with. Therefore you have a strong prior belief that the coin is fair. Youflip the coin 10 times and get 9 What is your predicted probability of heads for the 11th flip? Explain your answer carefully; justify your choice of prior.
(B)Now you have a different coin, this one made of some strange material and marked (in fine print) “Patent Pending, International Magic, ” You flip the coin 10 times and get 9 heads. What is your predicted probability of heads for the 11th flip? Explain your answer carefully; justify your choice of prior. Hint: Use the prior fromExercise 6.4.

更多其他:C++代写 java代写 r代写 代码代写 金融代写 python代写 web代写 物理代写 数学代写 考试助攻 C语言代写 计算机代写 finance代写 code代写 project代写
