Mathematics
Optimization
数学优化代写 2.2. Let 𝐴𝑋 = 0 be a homogeneous system, where 𝐴 is an 𝑚 × 𝑛 matrix. Knowing that the system has an infinite number of solutions
[4.0 points] 1.
Consider the system of linear equations:
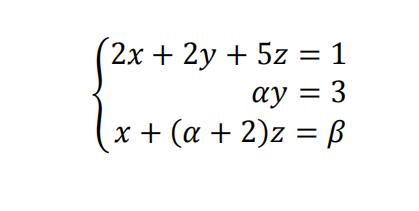
{2𝑥 + 2𝑦 + 5𝑧 = 1 𝛼𝑦 = 3
𝑥 + (𝛼 + 2)𝑧 = 𝛽
where 𝛼, 𝛽 ∈ ℝ are parameters.
(1.0) a) Write the system in the matrix form.
(2.0) b) Discuss the solution set based on the parameters 𝛼 and 𝛽.
(1.0) c) Determine the system solution for 𝛼 = 1 and 𝛽 = 0.
[6.0 points] 2. 数学优化代写
Indicate which one of the following propositions is correct.
(1.5) 2.1. Let A and B be two square matrices of order n. Then, the following equality is certainly verified:
(a) (𝐴 + 𝐵)(𝐴 − 𝐵) =𝐴2 − 𝐴𝐵 + 𝐵𝐴 − 𝐵2
(b) (𝐴 + 𝐵)2 = 𝐴2+ 2𝐴𝐵+𝐵2
(c) (𝐴 − 𝐵)2 = 𝐴2 − 2𝐴𝐵 + 𝐵2
(d) (𝐴𝐵)2 =𝐴2𝐵2
(1.5) 2.2. Let 𝐴𝑋 = 0 be a homogeneous system, where 𝐴 is an 𝑚 × 𝑛 matrix. Knowing that the system has an infinite number of solutions, which one of the following propositions is true?
i) The rank of matrix 𝐴 is less than 𝑛 ;
ii) The rank of matrix 𝐴 is less than 𝑚;
iii) 𝐴 is a square matrix (𝑚 = 𝑛) and its rank is equal to 𝑛;
iv) It is not possible to say anything about the rank of 𝐴.5
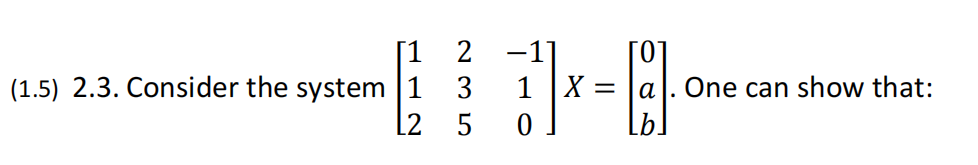
(a) The system has a unique solution if and only if 𝑏 = 𝑎;
(b) The system has a unique solution if 𝑎 = 𝑏 = 0;
(c) The system is not possible for 𝑎 = 𝑏 = 0;
(d) The system has an infinite number of solutions for 𝑎 = 𝑏 = 0.
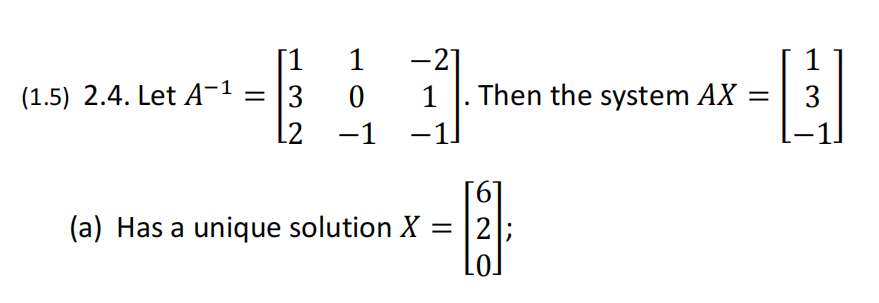
(b) Has an infinite number of solutions;
(c) Is not possible;
(d) Has only two solutions.
[4.0 points] 3. 数学优化代写
Consider the set of vectors in ℝ³, ℬ = {(1,0,1), (0,2,5), (0,1,3)}.
(1.5) a) Verify that ℬ is a basis of ℝ³.
(2.5) b) Which are the coordinates of the canonical basis of ℝ³ in the basis consisting of the elements of set ℬ?
Suggestion: Use the change of basis matrix to solve this question.
[4.0 points] 4. 数学优化代写
Consider the linear transformation 𝑇: ℝ4 → ℝ³,
𝑇(𝑥, 𝑦, 𝑧, 𝑤) = (𝑥 + 2𝑦 + 3𝑧 + 4𝑤, 2𝑥 + 𝑧 + 5𝑤, 6𝑥 + 4𝑦 + 8𝑧 + 18𝑤)
(1.0) a) Find the matrix representing the linear transformation in the canonical basis.
(2.0) b) Calculate dim(kerT) and find a basis for this linear subspace.
(1.0) c) Calculate dim (𝑅𝑎𝑛𝑔𝑒(𝑇)).
[2.0 points] 5.
Let A be a square 𝑛-matrix , with det 𝐴 = 1. Indicate if the following statements are true or false, justifying all your answers :
a) 𝐴T∙ 𝐴 = 𝐼;
b) The lines of A form a basis of ℝn ;
c) The columns of A are a linearly independent set of vectors;
d)The dimension of ker(A) is equal to 1.

其他代写:homework代写 java代写 matlab代写 program代写 project代写 finance代写 python代写 essay代写 report代写 paper代写 assignment代写 加拿大代写 作业代写 作业加急 北美代写 英国代写 北美作业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
