MATH 223FINAL EXAM STUDY GUIDE
数学代考推荐 If you start to move on the surface parallel to the y-axis in the direction of increasing y, does your height increase ordecrease?
1.A sonic boom carpet is a region on the ground where the sonic boom is heard directly from the airplane and not as a reflection. 数学代考推荐
The width of the carpet, W, can be expressed as a function of the air temperature on the ground directly below the airplane, t, and the vertical temperature gradient at the airplane’s altitude, d. Suppose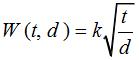 
for some positive constant k.
(a)If d is fixed, is the width of the carpet an increasing or decreasing function of t.
(b)If t is fixed, is the width of the carpet an increasing or decreasing function of d.
2.Describe the following sets of points in words, write an equation, and sketch agraph:
(a)The set of points whose distance from the line L is The line L is the intersection ofthe plane y = 3 and the xy-plane.
(b)The set of points whose distance from the yz-plane is three.
(c)The set of points whose distance from the z-axis and the xy-plane are equal.
3.By setting one variable constant, find a plane that intersects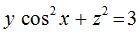 
in a :
(a) parabola (b) sinusoidal curve (c) line(s)
y cos2 x + z2 = 3
in a:
4.Consider thefunction f (x, y) = y – x2 .
(a)Plotthe level curves of the function for z = -2, -1, 0,1, 2 .
(b)Imagine the surface whose height above any point (x, y) is given by f (x, y) . Suppose you are standing on the surface at the point where x = 1, y = 2 .
(i)What is yourheight?
(ii)If you start to move on the surface parallel to the y-axis in the direction of increasing y, does your height increase ordecrease? 数学代考推荐
(iii)Does your height increase or decrease if you start to move on the surface parallel to the x– axis in the direction of increasingx?
(iv)Are you ascending or descending when you go from (1,2) in the direction making an angle of 3π/4 with thex-axis?
(v)Suppose you start to move in the direction you found in part (iv) at a rate of 3mph, at what rate is your height changing with respect to time.
5 (a) Describe the level curves(contour lines) for each of the following functions:
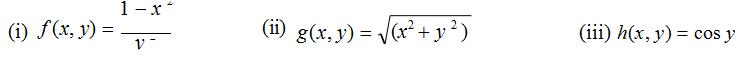
5 (b) Describe the level surfaces for each of the following functions:
6.The figure at the right shows the level curves of the temperature T in degrees Celsius as a function oft hours and depth h in centimeters beneath the surface of the ground from midnight ( t = 0 ) one day to midnight ( t = 24) the next.
(a)Sketch a graph of the temperature asa function of time at 20 centimeters.
(b)Sketch a graph of the temperature asa function of the depth at noon.
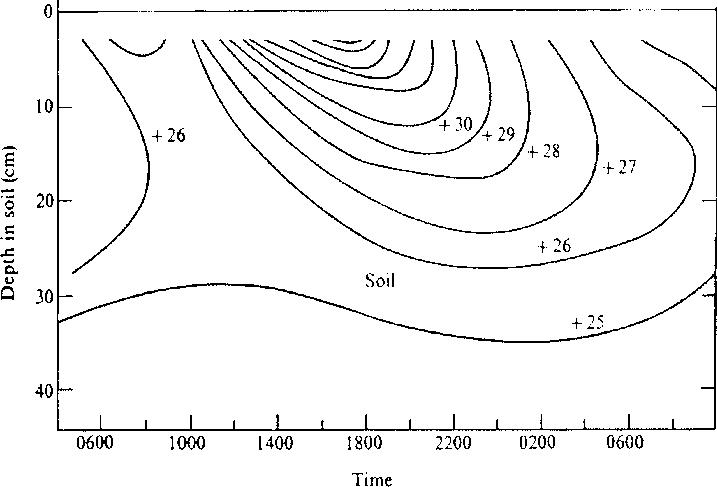
from S. J. Williamson, Fundamentals of Air Pollution, (Reading: Addison-Wesley, 1973)
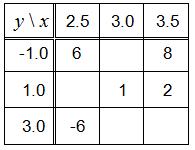
7.Given the table of some values of a linear function, complete the table and find a formula for the function.
8.Consider theplanes:
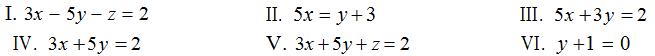
List all of the planes which:
(a)Are parallel to thez-axis.
(b)Areparallel to 3x = 5y + z + 7 .
(c)Contain the point (1, -1, 6).
(d)Arenormal to (2i + 3k )×(3i – k ) .
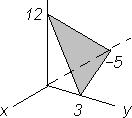
9.A portion of the graph of a linear function is shown.
(a)Find an equation for the linear shown.
(b)Find a vector perpendicular to the plane.
(c)Find the area of the shaded triangular region.
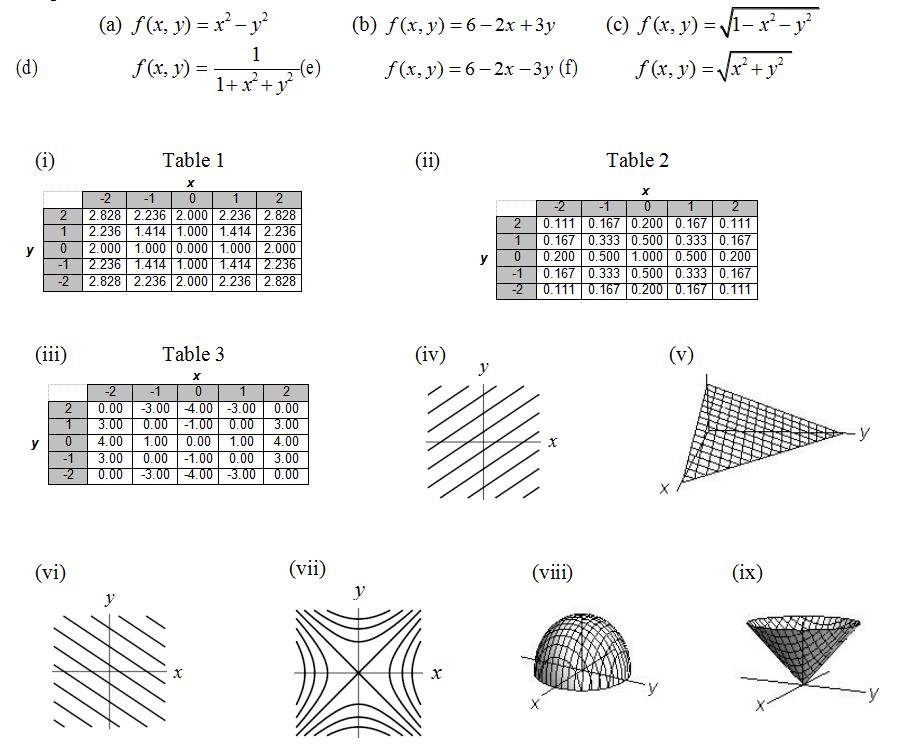
10.Match each of the following functions (a) – (f), given by a formula, to the correspondingtables, graphs, and/or contour diagrams (i) – (ix). 数学代考推荐
There may be more than one representation or no representations for a formula.
11.Letv = 3i + 2 j – 2k and w = 4i – 3 j + k . Find each of the following:
(a)A vector of length 5 parallel to w.
(b)A vector perpendicular to v but not perpendicular to w.
(c)v×w
The angle between v and w.
The component of v in the direction of w .
A vector perpendicular(orthogonal) to both v and w.
12.Consider the vectors u =2i – j + 3k and v = -2ai + aj – k .
(a)For what value(s) of a are u and vperpendicular? 数学代考推荐
(b)For what value(s) of a are u and vparallel?
(c)Find an equation of the plane normal to u and containing the point (1, -2,3).
(d)Find a parameterization for the line parallel to u and containing the point(1, -2,3).
13 (a) Find a vector parallel to the line of intersection of the two planes x + 2y – 3z = 7 and 3x = y – z(b) Find parametric equations for the line in part(a)
14.Find the following:
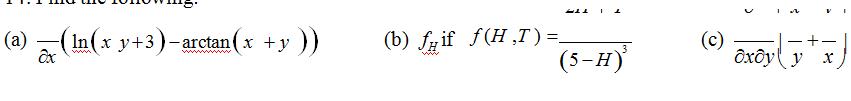
15.Find an equation for the tangent planeto:
(a)f (x, y) = yexy at (x, y) = (1, 2) (b) (x -1)2 + 4( y – 2)2 + (z – 3)2 = 17 at (3,3, 6)
16.A ball is thrown from ground level with initial speed v (m/sec) and at an angle of a with the horizontal. It hits the ground at a distance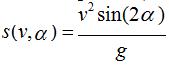 
where g = 9.8 m/sec2.
(a)Find the differential ds.
(b)What does the sign of sa(20,π3) tell you?
(c)Use the linearization of s about (20,p3) to estimate the change in a that is needed to get approximately the same distance if the initial speed changes to 19 m/sec.
17.The depth of a lake at the point (x, y) is givenby h(x, y) = 2x2 + 3y2 feet. A boat is at (-1,2).
(a)If the boat sails in the direction of the point (3,3) , is the water getting deeper orshallower? 数学代考推荐
(b)In which direction should the boat sail for the depth to remain constant? Give your answer asa vector.
(c)If the boat moves on the curve r (t) = (t2 -1)i + (t + 2) j for t in minutes, at what rate is the depth changing when t = 2 ?
18.Calculate thefollowing:
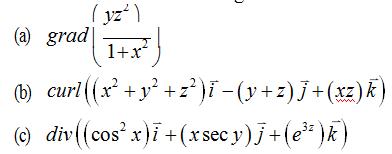
(d)The maximum rate of change of f (x, y, z) = tan x + at (π/4, 3,1).
(e)The directional derivative of f (x, y, z) = exy + z at the point (1, 1, 0) in the direction of 2i – 3 j + 4k.
(f)The potential function for G =yi + xj + ez cos(ez )k .
19.Which of the following vector fields are conservative? If they are conservative findthe corresponding potential function.
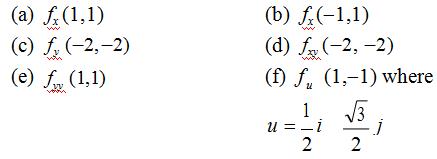
20.The contour plot for f (x, y) is shown at the right.
Determine if each quantity is positive, negative, or zero.
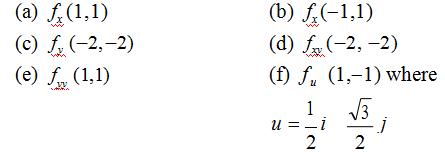
21.Letw(x, y) = 3x cos(π y) .
22.Asteel bar with circular cross section of radius 6 cm and length 50 cm is being heated. The radius and the length increases by .005 cm for each 1 degree centigrade rise in What is the rate of change in the volume of the steel bar?
23 (a) Find and classify all of the critical points for f (x, y) = 2x3 – 3x2 -12x + y3 + 3y2 – 9y .
(b) Find the quadratic Taylor polynomial of f (x, y) near the critical point, where the point is a local minimum of f (x, y) .
24.Let f (x, y) =Kx2 + y2 – 4xy .
(a)Verify that the point (0, 0) is a critical point.
(b)Determine the values of K, if any, for which (0, 0) can be classified as the following.
(i) a saddle point (ii) a local minimum (iii) a local maximum
25.Find an equation for eachsurface:
(a)x2 + y2 = 8 in cylindrical coordinates
(b) y = xin cylindrical coordinates
(c)
in spherical coordinates
(d)z = 10 in spherical coordinates
26.Determine (without calculation) whether the integrals are positive, negative, or zero. Let D be the region inside the unit circle centered at the origin, T be the top half of the region, B be the bottom half of the region, L be the left half of the region, and R be the right half of the
27.Evaluate each of theintegrals:
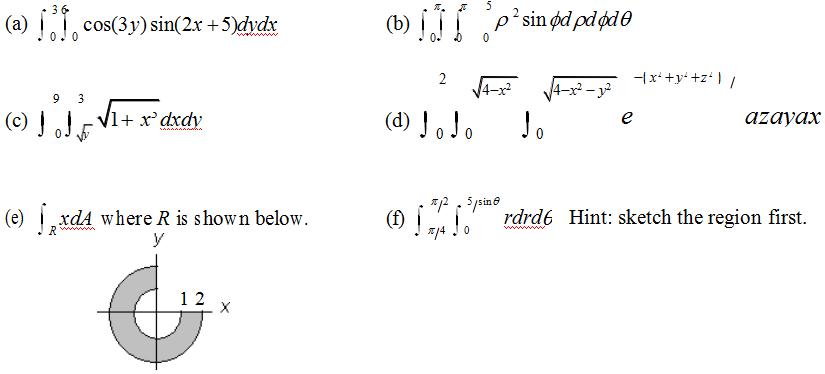
28.Set up integrals needed to find thefollowing:
(a)The volume between the sphere r= 2 and the cone z = r . (Cartesian, cylindrical, and spherical)
(b)The volume between x = 20 – y2 – z2 and x = y2 + z2 + 2 . (Cartesian and cylindrical)
(c)The volume of the solid in the first octant bounded from aboveby x2 + z2 = 16 and y = 12 .(Cartesian in the order dxdydz and Cylindrical in the order rdydrdq )
(d)The volume of the tetrahedron under the portion of the plane shown at the right, bounded by the planes y = 0 ,x = 0 , and z = 0 . (Cartesian) 数学代考推荐
29.A pile of dirt is approximately in the shape of an inverted cone of height 4m with base radius of 4m. The density of the dirt is proportional to the distance from the apex of the pile of dirt. Set upan integral for the mass of the dirt pile.
30.Give parametric equations for the followingcurves: 数学代考推荐
(a)A circle of radius 3 on theplane the origin. y = 1centered at (2,1, 0) oriented clockwise when viewed from origin.
(b)A line perpendicular to z =2x – 3y + 7 and through the point (1, -2,3) .
(c)The curve y = ( x + 2)3 oriented from (2, 64) to (0,8) .
(d)The intersection of thesurfaces z2 = x2 + y2 and z = 6 – x2 – y2 .
(e)The ellipse with major diameter 2a along the x-axis and minor diameter 2b along the y axis, centered at the origin.
(f)The intersection of thesurfaces 
31.A child is sliding down a helical slide. Her position at time t seconds after the start is given in feetby r = (3cos t )i + (3sin t ) j + (10 – t)k . The ground is the xy-plane.
(a)When is the child 6 feet from theground? 数学代考推荐
(b)How fast is the child traveling at 2seconds?
(c)At time t =2p seconds, the child leaves the slide tangent to the slide at that point. What is the equation of the tangent line?
32.The surface of a hill is representedby z = 12 – x2 – 3y2 , where x and y are measured horizontally.
A projectile is launched from the point (1,1, 7) and travels in a line perpendicular to the surface at that point.
(a)Find parametric equations for the path.
(b)Does the projectile pass through the point (1,1,8)?
33.Match the vector field to its
34.Given the plot of the vector field, F , list the following quantities in increasing order.
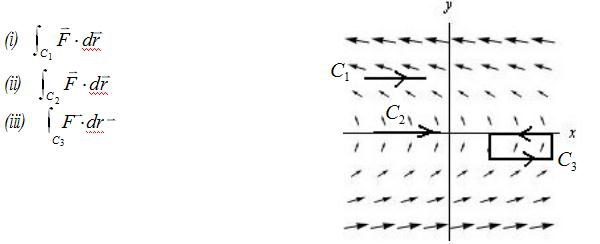
35.Evaluate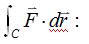
(a) F = (x + z)i + zj + yk . C is the line from (2, 4, 4) to (1,5, 2) .
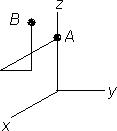
(b)F = x2i + z sin( yz) j + y sin( yz)k . C is the curve fromA(0, 0,1) toB(3,1, 2)as shown below.
(c)F =yi – xj + zk . C is the circle of radius 3 centered on the z-axis in the plane clockwise when viewed from above.
(d)F= 4x3i + (x + y) j . C is the curve y = sin(2x) from (0, 0) to (π/2, 0) .
(e)F= (- y3 + sin(x2 ))i + (x3 – ln( y2 +1)) j . C is the circle of radius 5 centered at (0, 0) in the xy-plane oriented counterclockwise.
(f)F = yi +rxj . C is the parameterized path r (t)= (2(3 – t) + sin(p t / 3))i + ((3 – t)2 + log(t 2 +1)) j,0 da≤ t ≤ 3 .
36.Calculate the flux of F through the surface, S, givenbelow:
(a) F = 3i + 4 j + (z – x)k . S is a square of side 2 on the plane z = x oriented upward.
(b)F = -5i + zj – yk . S is x =
for y2 + z2 for 0 ≤ x ≤ 8 , oriented in the negative x-direction. 数学代考推荐
(c)F =2xi -(z3 – y) j + (x5 + 7z)k . S is the closed cylinder centered on the y-axis with radius 3,length 5, oriented outward.
(d)F =xi + yj + zk .S is the part of the surface z = 25 -(x2 + y2 ) above the disk of radius 5 centered at the origin, oriented upward.
37.(a) Evaluate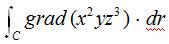 
grad (x2 yz3 ) × dr where C is the square of side 2 centered at (1,1) in the xy-plane,oriented counterclockwise.
(b)Evaluate 
where S is the cube of side 4 centered at (2,1,3) ,oriented outward.
(c)Evaluate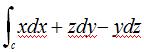 
where C is the circle of radius a in the yz plane centered at the origin,oriented clockwise when viewed from the positive x-axis.
38.Consider the flux of the vector field 
for p ≥ 0 out of the sphere of radius 5 centered at the origin. For what value of p is the flux a maximum? What is that maximum value?
39.Let S1 be the ellipsoid 4x2 + y 2 + 4z 2 = 64 and let S be the sphere x2 + y 2 + z 2 = 1, both oriented Let
r≠0.
(a)Find div F.
(b)Calculate the flux out of the sphere.
(c)Using the answers to part (a) and (b), find the flux out of the ellipsoid.
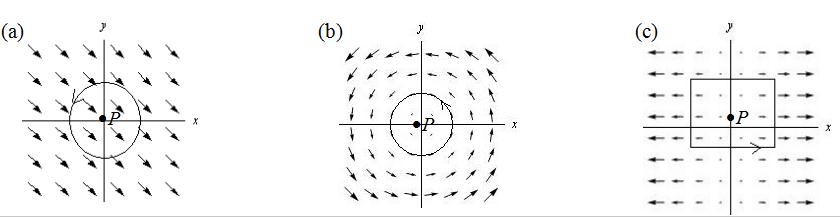
40.The vector fields below have theform F = F1i + F2 j . Assume F1 andF2 depend only on x and y. 数学代考推荐
For each vector field, circle the best answers.
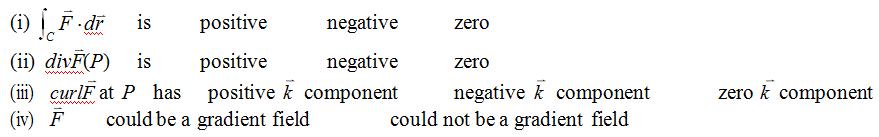
41.LetF = (75x – x3 )i – y3 j – z3k and let S , S , and S be spheres of radius 1, 5, and 6 respectively,centered at the origin.
(a)Where is divF =0 ?
(b)Without computing the flux, order the flux out of the spheres from smallest to largest.
42.In the region between the circles C : x2 +y2 = 4 and C2: x2 + y2 = 25 in the xy-plane, the vector field F has curlF = 3k . If C1 and C2 are both oriented counterclockwise when viewed from above,find the value of òC F × dr – òC F × dr .
43.A particle travels along the helix C givenby x = cos t, y = sin t, z = t,for 0 ≤ t ≤ 4p and is subject to a force F = – yi + xj + 5k . Find the total work done by the force for 0 ≤ t ≤ 4p . 数学代考推荐
44.Determine if each of the following quantities is a vector (V), a scalar (S), or is not defined(ND).Assume that u and v are 3-D vectors, , S is a smooth surface, C is a smooth curve, G is a differentiable 3-D vector field, and f is a differentiable scalar function of x, y, and z.
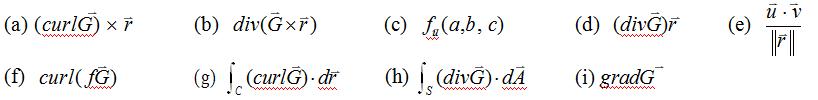
45.True orFalse?
(a)If all of the contours of a function g(x, y) are parallel lines, then the function must be linear.
(b)If curlF is parallel to the x-axis for all x, y, and z and if C is a circle in the xy-plane, then the circulation of F around C must be zero.
(c)If f is a differentiable function,then 
(d)If F is a divergence free vector field defined everywhere and S is a closed surface orientedinward,then 
(e)If G is a curl free vector field defined everywhere and C is a simple closed path, then 
46.Use the portion of the contour diagram of f (x, y) shown below to estimate the following:
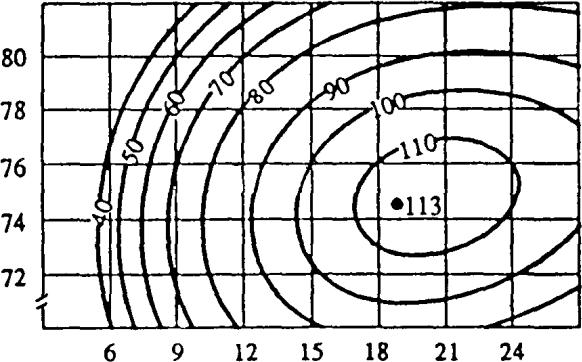
(a)gradf (15, 78)
(b)fu (15, 76) in the direction –i + j
(c) A critical point of f (x, y) .
48.(a) Suppose S is the surface obtained by taking the union of the upper hemisphere of radius 2 centered at (0, 0, 4) and an open cylinder of radius 2 centered around the z-axis, with 0 ≤ z ≤ 4 .If the orientation of S is away from the origin,evaluate the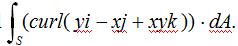
(b) Suppose S is an open cylindrical can of radius 4, centered along the x-axis, closed at x = -3 and open at x = 5. Let S be oriented away from the origin. If curlG = (x – z)i – yj – 2k, find 
where C is the boundary of S. 数学代考推荐
49.Suppose W is a solid consisting of cube and three solid cylinders of height 6 and radius 2. (See picture below.) The cube is centered at the origin and has side 5. One cylinder is centered on the z-axis and the other two cylinders are centered on the y-axis. Let S be the whole surface of W except for the circular disk of the cylinder centered on the z-axis with outward
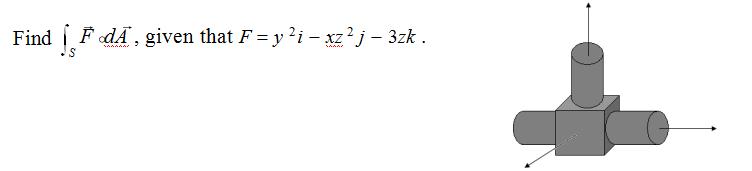
50.Consider theline L1 parameterized by r1(t) = (2 – t)i + (3 + 2t) j + (4 – 5t)k and the line L2 parameterized by True or False.
(a)Thelines L1 and L2 are perpendicular to each other. 数学代考推荐
(b)Theline L1 is normal to the plane 8x – y – 2z = 0 .
(c)Theline L2 is parallel to the plane x = 2y – 5z .
(d)Theline L2 is parallel to the vector -16i + 2 j .
(e)Theplane x + 4z – 29 = 0 contains the line L2 .
