数学代数代写 Algebra代写 math代写

MTH745U/P (2021–22)

Further Topics in Algebra

(Fields and Galois Theory)

Coursework 12

数学代数代写 Questions 1 and 2 are compulsory. You should hand them in before the tutorial next week.In addition to the exercises on the sheets,

Questions 1 and 2 are compulsory. You should hand them in before the tutorial next week.

In addition to the exercises on the sheets, you should also attempt those exercises embedded in the lecture notes, and any others you may come across or invent.

Time permitting, we will try to give feedback on at least some of your submissions, but maybe not all. If you would like feedback on a specific solution please indicate it in your submission.

Question 1 (For handing in). 数学代数代写

Let F be a finite field and let G be the group of invertible n × n upper triangular matrices with entries in F. Prove that G is a soluble group.

Question 2 (For handing in).

Give an example of a polynomial in Q[X] which is soluble by radicals, but whose splitting field is not an extension by radicals.

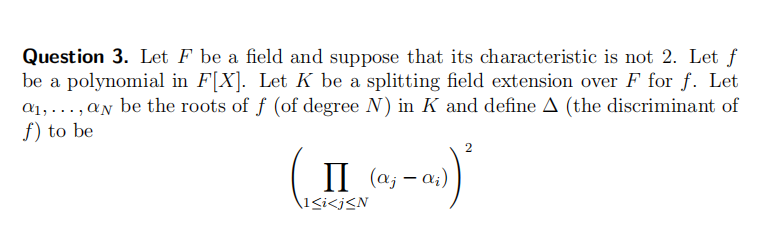
(1) Prove that ∆ is an element of F.

(2) Prove that if ∆ = 0, then f has a repeated root.

(3) Let S_N be the ‘symmetric’ group of permutations of {1 . . . , N} and let A_N be the subgroup of even permutations (this is often referred to as the alternating group). Seeing the Galois group G = Gal(K/F) of f over F as a subgroup of S_N , prove the following:

– if ∆ is non-zero and has a square root in F, then G is contained in A_N .

– if ∆ is non-zero but has no square root in F, then it has a square root in L. If this is the case, G is not contained in A_N and G ∩ A_N is index 2

in G. The fixed field of G ∩ A_N is the quadratic extension F(√ ∆) over F.

Question 4. 数学代数代写

Let F be a field and suppose that its characteristic is not equal to 2 or 3. Let f = X³ + aX + b be an irreducible cubic polynomial with coefficients a, b in F, and let K denote a splitting field extension over F for f.

(1) Prove that f is separable.

(2) Prove that the discriminant ∆ of f is −4a³ − 27b² and that it is non-zero.

Question 5. 数学代数代写

Find any textbook on Galois theory and learn how to solve an irreducible quartic polynomial (with coefficients in a field of characteristic not qual to 2 or 3) by radicals.

合作平台：essay代写论文代写写手招聘英国留学生代写