Math 185 Final Project (Due December 8)
Math代写 The baseball dataset consists of the statistics of 263 players in Major LeagueBaseball in the season 1986.The dataset (hitters.csv)
Problem 1 Math代写
The baseball dataset consists of the statistics of 263 players in Major League Baseball in the season 1986.
The dataset (hitters.csv) consist of 20 variables:
| Variable | Description | ||||
| AtBat | Number of times at bat in 1986 | ||||
| Hits | Number of hits in 1986 | ||||
| HmRun | Number of home runs in 1986Math代写 | ||||
| Runs | Number of runs in 1986 | ||||
| RBI | Number of runs batted in in 1986 | ||||
| Walks | Number of walks in 1986 Math代写 | ||||
| Years | Number of years in major leagues | ||||
| CAtBat | Number of times at bat during his career | ||||
| CHits | Number of hits during his career | ||||
| CHmRun | Number of home runs during his career | ||||
| CRuns | Number of runs during his career Math代写 | ||||
| CRBI | Number of runs batted in during his career | ||||
| CWalks | Number of walks during his career | ||||
| League | A factor with levels | A | (coded as 1) and | N | (coded as 2) indicating |
| player’s league at the end of 1986 | |||||
Division |
A factor with levels | E | (coded as 1) and | W | (coded as 2) indicating |
| player’s division at the end of 1986 | |||||
| PutOuts | Number of put outs in 1986Math代写 | ||||
| Assists | Number of assists in 1986 | ||||
| Errors | Number of errors in 1986 | ||||
| Salary | 1987 annual salary on opening day in thousands of dollars | ||||
| NewLeague | A factor with levels | A | (coded as 1) and | N | (coded as 2) indicating |
| player’s league at the beginning of 1987 | |||||
In this problem, we use Salary as the response variable, and the rest 19 variables as predictors/covariates, which measure the performance of each player in season
1986 and his whole career. Write R functions to perform variable selection using best subset selection partnered with BIC (Bayesian Information Criterion):
1)Starting from the null model, apply the forward stepwise selection algorithmto produce a sequence of sub-models iteratively, and select a single best model using the Plot the “BIC vs Number of Variables” curve. Present the selected model with the corresponding BIC.Math代写
2)Starting from the full model (that is, the one obtained from minimizing the MSE/RSS using all the predictors), apply the backward stepwise selection algorithm to produce a sequence of sub-models iteratively, and select a single best model using the BIC. Plot the “BIC vs Number of Variables” curve. Present the selected model with the corresponding
3)Are the selected models from 1) and 2) the same?

Problem 2 Math代写
In this problem, we fit ridge regression on the same dataset as in Problem 1. First,
standardize the variables so that they are on the same scale. Next, choose a grid of
λ values ranging from λ= 1010 to λ = 10−2, essentially covering the full range of scenarios from the null model containing only the intercept, to the least squares fit. For example:
> grid = 10^seq(10, -2, length=100)Math代写
1)Write an R function to do the following: associated with each value of λ , compute a vector of ridge regression coefficients (including the intercept), stored in a 20 × 100 matrix, with 20 rows (one for each predictor, plus an intercept) and 100 columns (one for each value ofλ).
2)To find the “best”λ , use ten-fold cross-validation to choose the tuning parameter from the previous grid of values. Set a random seed – set.seed(1), firstso your results will be reproducible, since the choice of the cross-validation folds is Plot the “Cross-Validation Error versus λ” curve, and report the selected λ.
3)Finally, refit the ridge regression model on the full dataset, using the value ofλ chosen by cross-validation, and report the coefficient estimates.Math代写
Remark: You should expect that none of the coefficients are zero – ridge regression does not perform variable selection.
Problem 3 Math代写
In this problem, we revisit the best subset selection problem. Given a response
vector Y = (𝑦1, … ,𝑦n)t and an n× p design matrix X= (x1, … , xn)t with xi =
(x1, … , xip) . For 1 ≤ k ≤ p, let β0, β be the solution to the following sparsity-
constrained least squares problem:
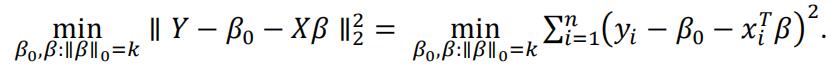
Based on the property β0 = y − xtβ, we can center Y and X first to get rid of the intercept, and solve
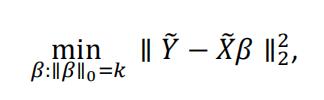
where y and x represent the centered y and x, respectively. To solve this, we introduce the Gradient Hard Thresholding Pursuit (GraHTP) algorithm. Let f(β) =
∥ y − xβ ∥2⁄(2n) be the objective function.
GraHTP Algorithm.
Input:y, x, sparsity k, stepsize n > 0Math代写
(Hint: normalize the columns of x to have variance 1). Initialization: β0 = 0, t = 1.
repeat
1) Compute βt = βt−1 − n∇f(βt−1);
2) Let St = supp(βt, k) be the indices of βt with the largest k absolute values; 3) Compute βt = argmin{f(β); supp(β) ⊆ St};
t = t + 1;Math代写
until convergence, i.e. ∥ βt − βt−1 ∥2< 10−4.
Output: βt.Math代写
1)Write an R function to implement the above GraHTP
2)Consider again the baseball dataset in Problem 1 with n= 263, p = 19. For k = 1, … , p, use the above function to find the best k-sparse model, denoted by ℳk.Then use BIC to select a single best model among ℳ1, … , ℳp.
3)Compare your result with those obtained in Problem1.

其他代写:考试助攻 计算机代写 java代写 algorithm代写 代写CS function代写 C/C++代写 paper代写 r代写 金融经济统计代写 matlab代写 web代写 数学代写 金融经济统计代写 essay代写
