数学习题代写 Maths代写 equation代写

LI-Maths

数学习题代写 1. Let H be a general Hermitian matrix with TrH = 0 and detH = −1. (a) Show that any such a matrix can be represented as

1. 数学习题代写

Let H be a general Hermitian matrix with TrH = 0 and detH = −1.

(a) Show that any such a matrix can be represented as

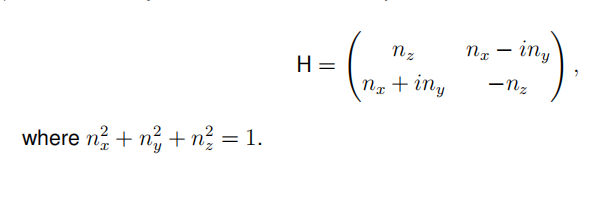
(b) Show that H is a unitary matrix.

(d) Since n = n_xi + n_yj + n_xk is a unit vector, it is convenient to represent its components in spherical polar coordinates (θ, φ). Show that the matrix H in this representation is

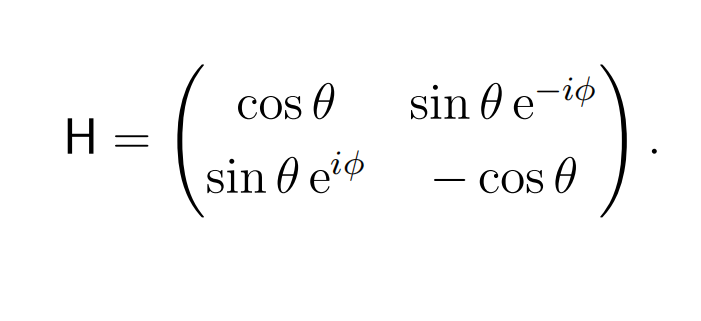
(e) Diagonalise H with a unitary transform, Λ = U†HU, choosing the transformation matrix U to be of the same form as H. Given θ and φ in H, fifind the corresponding values of parameters in U. Verify your answer.

2. 数学习题代写

Consider the following matrix:

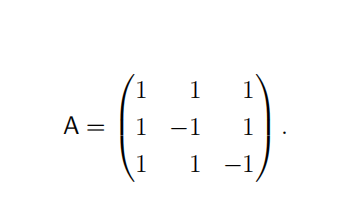
(a) Find its eigenvalues and eigenvectors.

(b) Diagonalise A with a similarity transform, Λ = P⁻¹AP.

(c) Use the diagonalisation to calculate an arbitrary odd power A²ⁿ⁻¹ (where n = 1, 2, · · · ). Check that your answers reproduces matrix A when n = 1.

(d) Find a square root of A, i.e. any one matrix M such that M² = A. Verify your answer by explicitly calculating matrix elements {M²}_ij and showing your work in detail.