CSC336H1 Homework 1
数值方法课业代写 1.Let f(x) denote the function sin((x + 1/4)π). (a) What is the condition number of f(n), when n is an integer? (b) What is the exact value of f(n)
1.
Let f(x) denote the function sin((x + 1/4)π).
(a) What is the condition number of f(n), when n is an integer?
(b) What is the exact value of f(n), when n is an integer?
(c) How many digits do you lose in evaluating f(n) for n = 10? How about for n = 104? n = 108? n = 1012? n = 1016?
2. 数值方法课业代写
Suppose that a, b, and c are all real numbers, and that b2> 4ac. The two solutions to the equation ax2+ bx + c = 0 are given by the quadratic formula
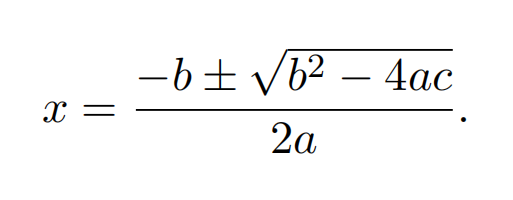
(a) Under what conditions can cancellation error decrease the precision of your solution when it is computed using this formula?
(b) Is there an alternative formula that could be used to represent the two solutions? (Hint: try replacing x with 1/y and solving for y).
(c) How would you use both of these formulas to compute the solutions without any loss of precision? (Hint: use one formula for one of the two solutions, and the other formula for the other solution).

(b) Use the comparison technique to accelerate the convergence of this series. How many terms of the new series must be summed up to evaluate the sum to 5 significant digits?
(c) Use the Euler-Maclaurin summation formula, starting at n = 4, to accelerate the convergence of this series. How many terms in the Euler-Maclaurin formula must be summed up to evaluate the sum to 5 significant digits? Hint: Recall that ∫1/(x2 + 1) dx = arctan(x).
4. 数值方法课业代写
The derivative of a function f(x) at x can be approximated by the formula
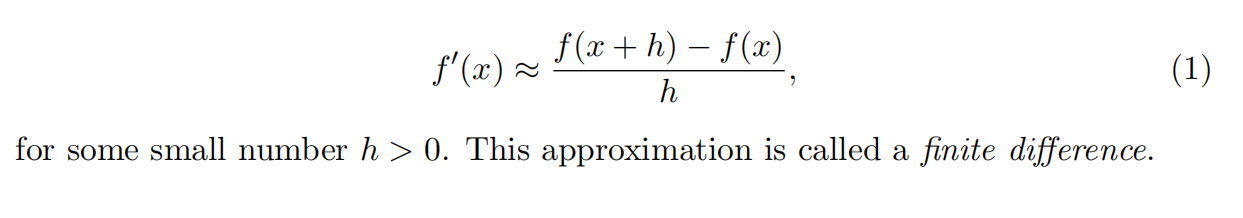
(a) What happens to the precision of the approximation as h approaches zero?
(b) What happens to the precision of the approximation if h is large?
(c) Suppose that f’(x) and f’’(x) are both between −2 and 2. If we are working in double precision, which value of h produces the most precise approximation to f’(x)? (Hint: look at the Taylor series of f(x) at x).
(d) What is the maximum number of significant digits we can expect in the approximation if we are working in double precision?

(a) What is the maximum accuracy one can obtain when using this power series?
(b) How many terms must one take to obtain this maximum accuracy?
(c) What is the size of the largest term in this sum?
(d) What is the largest value of x for which this power series expansion yields full double precision accuracy?

Suppose that N = 5. How does the relative error of the truncated series behave as x → ∞? How about for N = 10? N = 15? (Hint: compare the truncated series to the exponential integral provided by MATLAB in the function expint and by SciPy in the function scipy.special.exp1).

