MATH 5640/6640 – Introduction to Numerical Analysis II
Homework 4
数值分析导论代写 There are totally 4 problems (2 pages). Submit the code for Problems 3 and 4 in the appendix. Problem 1 [35 points]Given the linear system Ax = b
There are totally 4 problems (2 pages). Submit the code for Problems 3 and 4 in the appendix.
Problem 1 [35 points] 数值分析导论代写
Given the linear system Ax = b where
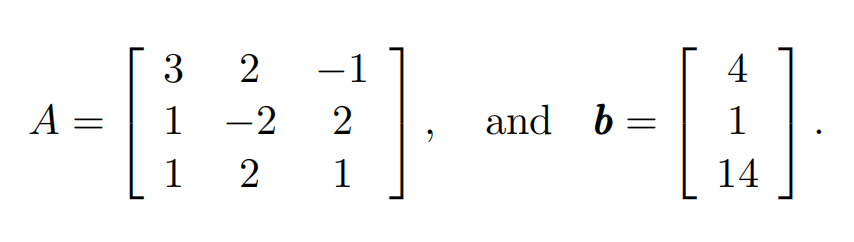
(a) Apply the Gaussian elimination method to solve the linear system.
(b) Based on the Gaussian elimination obtained in (a), perform the LU decomposition of the matrix A. Express L and U explicitly, and compare A and the product LU.
(c) Based on the lower triangular matrix L and the upper triangular matrix U that you obtain in (b), apply the forward substitution to solve Ly = b and the backward substitution to solve Ux = y. Compare with the solution that you obtain in (a).
Problem 2 [15 points] 数值分析导论代写
Given the matrix
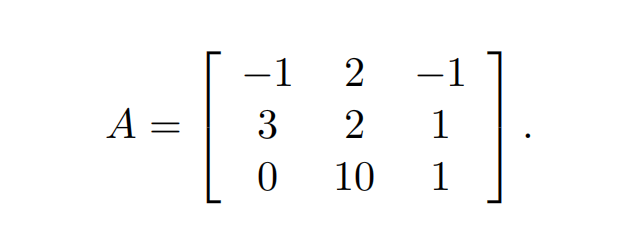
Following steps (a) and (b) to obtain the LU decomposition of the matrix A with partial pivoting.
(a) Apply the Gaussian elimination method with partial pivoting to obtain an upper triangular matrix U. Record the corresponding permutation matrix for each pivoting step, and the numbers lik used to eliminate the zeros in column k.
(b) Based on (a), express the matrices P, L and U explicitly in the decomposition
P A = LU,
where P is a permutation matrix, L is a lower triangular matrix, and U is an upper triangular matrix.

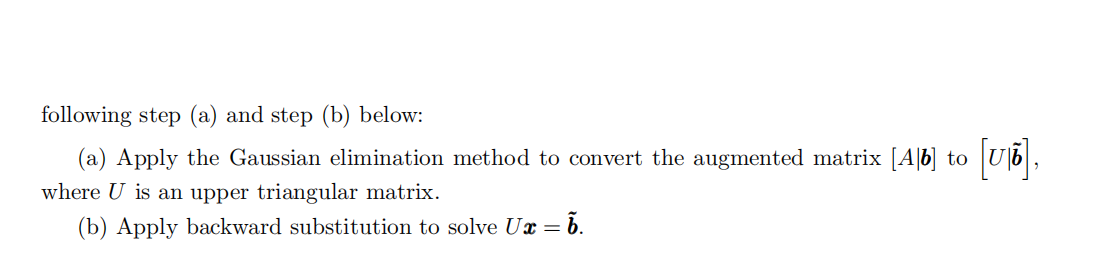
Problem 4 [25 points] (Coding) 数值分析导论代写
Solve the same linear system Ax = b as in Problem 3 but now using the LU decomposition:
(a) Revise the code in Problem 3 properly to obtain the LU decomposition of the matrix A (you need to define a new matrix to store the elements in L).
(b) Apply forward substitution to solve Ly = b.
(c) Apply backward substitution to solve Ux = y. Compare the solution you obtain with the one in Problem 3.

更多代写:CS网课exam代考价格 gmat保分 英国生物学网课代考 网课代写essay作业 微观经济学写作 找经济学代写
