Microeconomics代写 function代写 mathematics代写

Microeconomics I

Jehle and Reny (2011) Chapter 3 Theory of the Firm

Microeconomics代写 in its output market: takes p as given•in its input markets: takes w as giventhe definitions apply regardless of the number of firms notes

Takumi Naito^∗ Waseda University

October 1, 2019

Contents Microeconomics代写

1 Primitive Notions

1

2 Production             2

2.1 Returns to Scale and Varying Proportions . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

3 Cost                          4

4 Duality in Production                           8

5 The Competitive Firm                          8

5.1 Profifit Maximization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

5.2 The Profifit Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

1 Primitive Notions

the producer’s proftt  maximization problem:

• y:output
• x= (x₁, …, x_i, …, x_n)^T : input vector (input bundle)
• π:proftt
• p: outputprice
• w= (w₁, …, w_i, …, w_n)^T : input price vector
• f (x): production function (maximum output forx)

a firm behaves under perfect competition:

∗E-mail:  <tnaito@waseda.jp>; homepage:  <http://www.f.waseda.jp/tnaito>.

• in its output market:  takes p asgiven
• in its input markets:  takes w asgiven

the definitions apply regardless of the number of firmsMicroeconomics代写

notes:

• whymaximize profit?  → for the firm’s owners (typically consumers)
• for more details of (mainly non-competitive) firm behavior, studyindustrial organization

2 Production Microeconomics代写

standard properties of production function f (x) (assumed throughout):

• continuous: the graph of f (x) does not have any jumpingpart
• strictlyincreasing: f (x¹) > f (x⁰) for x¹ ≫ x⁰.

(⇐ f_i(x) > 0∀i: marginal product of input i is positive)

• strictlyquasiconcave:  f ((1 − t)x¹ + tx²) > min[f (x¹), f (x²)]∀x¹, x², x² ƒ= x¹∀t ∈ (0, 1).
• no free lunch: f (0ⁿ) =0.

a production function is mathematically the same as a utility function JR Figure 3.1:

• isoquantcurve Q(f (x⁰)) ≡ {x|x ∈ Rⁿ , f (x) = f (x⁰)}:  the set of x giving the same output as x⁰
• f(x) is strictly increasing ⇒ each isoquant curve is downward-sloping
• f(x) is strictly quasiconcave ⇒ each isoquant curve is strictly convex to the origin
• MRT S_ij(x) ≡ −dx_j/dx_i|_dy=0 = f_i(x)/f_j(x):  marginal  rate of technical  substitution of input i for input j

(absolute value of the slope of an isoquant curve from the i-axis):

• how many units of input jone must increase by decreasing one unit of input i
• howmany units of input j one can decrease to increase one unit of input i (technical value)Microeconomics代写

• f (x) is strictly quasiconcave ⇒ diminishing marginal rate of technical substitution Deftnition1 (The Elasticity of Substitution) The elasticity of substitution between inputs i and j:¹

ES_ij(x) ≡ −∂ ln(x_i/x_j)/∂ ln(w_i/w_j).

1 You should check that this is the same as JR Definition 3.2 by considering JR (3.2).

2.1 Returns to Scale and Varying Proportions

economic definitions of short run and long run:

• in the short run, at least one input isfixed;
• in the long run, all inputs arevariable

they are distinguished in terms of variability of inputs, not time period JR Figure 3.3:

• returnsto scale: how output changes when all inputs are changed in the same proportion (i.e., along a ray from the origin)

• returns to varying proportions: how output changes when only a part of inputs are changed (so that input proportionschange)

Deftnition 2 ((Global) Returns to Scale) f (x) has (global):Microeconomics代写

• increasing returns  to  scale  (IRS): f (tx) > tf (x)∀t > 1∀x;
• constant returns  to  scale  (CRS): f (tx) = tf (x)∀t > 0∀x;
• decreasing returns  to  scale  (DRS): f (tx) < tf (x)∀t > 1∀x.

f (x) is homogeneous of degree k:

Theorem 1 ((Shephard) Homogeneous Production Functions are Concave) Suppose that f (x) is homogeneous of degree k ∈ (0, 1]. Then f (x) is concave in x. In particular, if k ∈ (0, 1), then f (x) is strictly concave in x.

Proof. Proof for k = 1 is straightforward by just following the proof of JR Theorem 3.1.

For k ∈ (0, 1], let:

f (x) = (f (x)^1/k)^k = g^k ≡ F (g); g ≡ f (x)^1/k ≡ g(x).

First, since F ^′(g) = kg^k−1 > 0, F ^′′(g) = k(k − 1)g^k−2 ≤ 0, F (g) is concave in g from Theorem 12, Math Apps. Second, since f (x) is homogeneous of degree k, we have:

f (tx) = t^kf (x)

f (tx)^1/k = (t^kf (x))^1/k

= tf (x)^1/k

g(tx) = tg(x).Microeconomics代写

This implies that g(x) is homogeneous of degree one, and hence concave in x.

Since both F (g) and g(x) are concave, their composite function f (x) = F (g(x)) is concave. Specifically:

f ((1 − t)x¹ + tx²) = F (g((1 − t)x¹ + tx²))

≥ F ((1 − t)g(x¹) + tg(x²)) ( ∵ F (g) is increasing in g, g(x) is concave in x)

≥ (1 − t)F (g(x¹)) + tF (g(x²)) ( ∵  F (g) is concave in g)

= (1 − t)f (x¹) + tf (x²).

In particular, if k ∈ (0, 1), then F ^′′(g) = k(k − 1)g^k−2 < 0, implying that F (g) is strictly concave in g from Theorem 12, Math Apps. Since the weak inequality in the third line of the above displayed equation is now replaced by the strong inequality from Definition 13, Math Apps, we conclude that f (x) is strictly concave in x.

3 Cost Microeconomics代写

the producer’s cost minimization problem:

the cost minimization problem is mathematically the same as the expenditure minimization problem

JR Figure 3.4:

necessary conditions for the solution x^∗:

• minimumoutput constraint is satisfied with equality: f (x) = y (what if f (x) > y?)
• iso-costline is tangent to isoquant curve:  w_i/w_j = M RT S_ij(x^∗) (what if w_i/w_j ≷ M RT S_ij(x^∗)?) Lagrangian method (see section 7.2, Math Apps):

f (x) ≥ y y − f (x) ≤ 0

L(x, λ) ≡ w · x + λ(y − f (x)).

w · x is strictly increasing ⇒ y − f (x) ≤ 0 is satisfied with equality:

L_i(x, λ) = w_i − λf_i(x) = 0, i = 1, …, n, (1)

L_λ(x, λ) = y − f (x) = 0. (2)

(1):

w_i/w_j = f_i(x)/f_j(x), i, j = 1, …, n. (3)

• (2), (3) are the same as the two necessary conditions in JR Figure4
• w x is linear (⇒ quasiconvex), f (x) is strictly quasiconcave ⇒ (1), (2) are sufficient (see section 7.4, Math Apps)

the producer’s cost function:

c(w, y) ≡  min {w · x|f (x) ≥ y} ≡ w · x(w, y).

x Rn

+

• x(w, y): conditional input demand function

JR Figure 3.4:

• c(w,y) corresponds to the iso-cost line at the solution x^∗ = x(w, y)

Theorem 2 (Properties of the Cost Function) c(w, y) is:  1. c(w, 0) = 0;

1. c(w, 0) = 0;
2. continuous;
3. strictly increasing iny;
4. increasing inw;
5. homogeneous of degree one inw;
6. concave inw;
7. satisfies Shephard’slemma:

∂c(w, y)/∂w_i = x_i(w, y), i = 1, …, n.

Note that only property 7 requires differentiability.

Proof. See proof of JR Theorem 3.2.

additional property:

c(w, y) ≡ w · x(w, y):

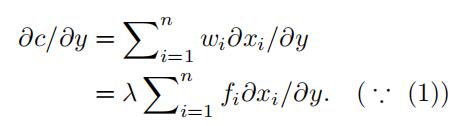
f(x(w, y)) ≡ y:

notes:

• economic meaning of λ: the value of relaxing (or tightening) the constraint (i.e.,marginal cost)
• economic meaning of concavity of c(w, y) inw:

even if w_i increases, c increases less than linearly (∵ x adjusts to minimize c)

Theorem 3 (Properties of Conditional Input Demands) .

1. x(w, y) is homogeneous of degree zero inw;
2. The substitutionmatrix:

is symmetric and negative semidefinite:

z^T σ(w, y)z ≤ 0∀z ∈ Rⁿ.

In particular, ∂x_i(w, y)/∂w_i ≤ 0, i = 1, …, n.Microeconomics代写

Deftnition 3 (Homothetic Functions) A real-valued function h(x) is homothetic if it is a composite function of an increasing function and a linearly homogeneous (i.e., homogeneous of degree one) function (see JR Exercise A2.10, p. 612):

h(x) = g(f (x)); g^′(f ) > 0, f (tx) ≡ tf (x)∀t > 0.

Theorem 4 (Cost and Conditional Input Demands when Production is Homothetic) .

1. When the production function ishomothetic:

(a)thecost function is multiplicatively separable in w and y: c(w, y) = c(w, 1)h(y), where c(w, 1) is the unit cost function, and h^′(y) > 0;

(b)theconditional input demand function is multiplicatively separable in w and y: x(w, y) = x(w, 1)h(y),where x(w, 1) is the unit input demand function.

2. When the production function is homogeneous of degree k >0,

(a)  c(w, y) = c(w, 1)y^1/k;

(b)  x(w, y) = x(w, 1)y^1/k.

Proof.Microeconomics代写

For 1., see proof of JR Theorem 3.4. In particular, if the production function is given by y = F (x) =f (g(x)), where f ^′(g) > 0, g(tx) ≡ tg(x)∀t > 0, h(y) is defined as h(y) ≡ f ⁻¹(y)/f ⁻¹(1).

Here we just show that f ⁻¹(y) >  0∀y  >  0, which is left as JR Exercise 3.5.  We  first have F (0ⁿ) = f (g(0ⁿ)) = 0 from no free lunch for F (x). Also, g(0ⁿ) = g(0 · x) = 0 · g(x) = 0, where the second equality follows from linear homogeneity of g(x). They imply that f (0) = 0.

Next, take any x such that g(x) > 0. Then:

y = F (x) = f (g(x)) > f (0) = 0 ( ∵ f ^′(g) > 0, f (0) = 0)

f ⁻¹(y) = g(x) > 0∀y > 0.

For 2., let F (x) be homogeneous of degree k > 0. Then:

F (x) = (F (x)^1/k)^k = g^k ≡ f (g); g ≡ F (x)^1/k ≡ g(x),

where f ^′(g) > 0, g(tx) ≡ tg(x)∀t > 0 (see proof of Theorem 1).  Taking the inverse of y = f (g) = g^k gives

g = f ⁻¹(y) = y^1/k, and hence h(y) ≡ f ⁻¹(y)/f ⁻¹(1) = y^1/k.

Example 1Microeconomics代写

when the production function is homogeneous of degree k > 0:

marginal cost and average cost:

M C(w, y) ≡ ∂c(w, y)/∂y = c(w, 1)(1/k)y^1/k−1,

AC(w, y) ≡ c(w, y)/y = c(w, 1)y^1/k−1.

• IRS(k > 1): M C(w, y) < AC(w, y), ∂M C(w, y)/∂y < 0, ∂AC(w, y)/∂y < 0
• CRS (k= 1): M C(w, y) = AC(w, y) = c(w, 1), ∂M C(w, y)/∂y = ∂AC(w, y)/∂y = 0
• DRS(k < 1): M C(w, y) > AC(w, y), ∂M C(w, y)/∂y > 0, ∂AC(w, y)/∂y > 0

short-run cost minimization:

x = (x^v, x^f ):

• x^v: variable inputs (w/ their pricesw^v)
• x^f: ftxed inputs (w/ their prices w^f )

short-run (or restricted) cost function:

sc(w^v, w^f , y; x^f ) ≡ min{w^v · x^v + w^f · x^f |f (x^v,x^f ) ≥ y} ≡ w^v · x^v(w^v, w^f , y; x^f ) + w^f · x^f .

• w^v x^v(w^v, w^f , y; x^f ): variable cost
• w^f x^f : ftxed cost

JR Figure 3.5:

• input 1 is variable, input 2 is fixed atx₂
• y¹:

–short-run: A:sc(y¹)

– long-run: B: c(y¹) < sc(y¹) (∵ x₂(y¹) = x^′ ƒ= x₂)Microeconomics代写

• y²:

–short-run: C:sc(y²)

– long-run: C: c(y²) = sc(y²) (∵ x₂(y²) = x₂)

• y³:

–short-run: E:sc(y³)

–  long-run: D: c(y³) < sc(y³) (∵ x₂(y³) = x^′′ ƒ= x₂)

relationships between short- and long-run cost functions:

• sc(w^v,w^f , y; x^f ) ≥ c(w^v, w^f , y)
• sc(w^v,w^f , y; x^f ) = c(w^v, w^f , y) ⇔ x^f = x^f (w^v, w^f , y)

JR Figure 3.6:

• sc(y;x^′ ) ≥ c(y), sc(y¹; x^′ ) = c(y¹)
• sc(y;x₂) ≥ c(y), sc(y²; x₂) = c(y²)
• sc(y;x^′′) ≥ c(y), sc(y³; x^′′) = c(y³)

∴ long-run cost curve is the lower envelope of short-run cost curves

4 Duality inProduction

5 The CompetitiveFirm Microeconomics代写

5.1ProfitMaximization

the producer’s profit maximization problem:

 

direct method:

indirect (two-step) method:

step 1: derive the cost function c(w, y)

step 2:

when does each method tend to be used?

• direct method: macroeconomics, where supplies of x areendogenous
• two-step method: industrial organization, where there are strategic interactions acrossfirms

direct method:

FOCs:

∂π/∂x_i = pf_i(x) − w_i = 0, i = 1, …, n. (4)

(4):

f_i(x)/f_j(x) = w_i/w_j, i, j = 1, …, n. (see (3)) (5)

Theorem 5 (Returns to Scale and Sufficiency of the FOCs) .

1. under either CRS or DRS, (4) is sufficient forprofit
2. under DRS, a solution to (4) is

Proof. For 1., Theorem 1 implies that f (x) is concave in x under either CRS or DRS. Since −w · x is linear and hence concave in x, π(x) = pf (x) − w · x is concave in x. Then, from Theorem 24, Math Apps, (4) is sufficient for profit maximization.

For 2., Theorem 26, Math Apps implies that a solution to (4) is unique.

indirect (two-step) method:

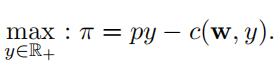
FOC (see Theorem 28, Math Apps):

∂π/∂y = p − ∂c(w, y)/∂y ≤ 0, y ≥ 0, y(p − ∂c(w, y)/∂y) = 0. (6)

SOC (see Theorem 21, Math Apps, for n = 1):

∂²π/∂y² = −∂²c(w, y)/∂y² ≤ 0 ⇔ ∂M C(w, y)/∂y ≥ 0. (7)

Example 2 (see Example 1)

when the production function is homogeneous of degree k > 0:

M C(w, y) ≡ ∂c(w, y)/∂y = c(w, 1)(1/k)y^1/k−1,

AC(w, y) ≡ c(w, y)/y = c(w, 1)y^1/k−1.

(7):

∂M C(w, y)/∂y ≥ 0 ⇔ k ≤ 1.

• IRS (k > 1): deviating from p = M C(w, y) increases π → FOC is not sufficient; nosolution
• CRS (k =1):

– p > c(w, 1): no solution

– p = c(w, 1): y^∗ ∈ [0, ∞) ⇒ π^∗ = 0

– p < c(w, 1): y^∗ = 0 ⇒ π^∗ = 0

• DRS (k < 1): deviating from p = M C(w, y) decreases π →FOC is sufficient; unique solution
• The ProfitFunction

assume: DRS (k < 1) (4):

• input demand function: x^∗= x(p, w)
• outputsupply function: y^∗ = f (x(p, w)) ≡ y(p, w) the proftt function:

π(p, w) ≡ max Microeconomics代写

y∈R+,x∈Rⁿ

{py − w · x|f (x) ≥ y} ≡ py(p, w) − w · x(p, w).

Theorem 6 (Properties of the Proftt Function) π(p, w) is continuous and:

1. increasing inp;
2. decreasing inw;
3. homogeneous of degree one in (p,w);
4. convex in (p,w);
5. satisfies Hotelling’slemma:

∂π(p, w)/∂p = y(p, w), ∂π(p, w)/∂w_i = −x_i(w, y), i = 1, …, n.

Note that only property 5 requires differentiability.

Proof. See proof of JR Theorem 3.7.

alternative proof of properties 4 and 5: left as exercises note:

• economic meaning of convexity of π(p, w) in (p,w):Microeconomics代写

even if p increases, π increases more than linearly (∵ y, x^h adjusts to maximize π)

Theorem 7 (Properties of Output Supply and Input Demand Functions) .

1. y(p, w) and x(p, w) are homogeneous of degree zero in (p,w);
2. The substitutionmatrix:

is symmetric and positive semidefinite:

z^T σ(p, w)z ≥ 0∀z ∈ Rⁿ.

In particular, ∂y(p, w)/∂p ≥ 0, ∂x_i(w, y)/∂w_i ≤ 0, i = 1, …, n.

short-run profit maximization (indirect method):

FOC:

max : π = py − sc(w^v, w^f , y; x^f ).

y∈R+

∂π/∂y = p − ∂sc(w^v, w^f , y; x^f )/∂y = 0.

a popular (but not always true) assumption in introductory/intermediate microeconomics: fixed cost is sunk: the firm has to pay the fixed cost even if the firm shuts down

no shut down condition:Microeconomics代写

revenue − variable cost − fixed cost ≥ − fixed cost revenue − variable cost ≥ 0

revenue ≥ variable cost price ≥ average variable cost

其他代写：algorithm代写 analysis代写 app代写 assembly代写 assignment代写 C++代写 code代写 course代写 dataset代写 java代写 web代写 北美作业代写 编程代写 考试助攻 program代写 cs作业代写 source code代写 dataset代写 finance代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写