F2018 Eduardo Mart´ın-Mart´ınez AMATH 473/AMATH 673/PHYS 454 Assignment 2
应用数学作业代写 There will be no late assignments accepted and that includes any kind of technical problems with Crowdmark, so I recommend handing in the day
Assignment 2
Due October 21th
This assignment is due on Friday, October 18th by 11:59pm (A minute before midnight).There will be no late assignments accepted and that includes any kind of technical problemswith Crowdmark, so I recommend handing in the day before to avoid this kind of problem!!! Please do not email the TAs or the Professor asking for a late assignment hand-in.
1 Some Photon BS (marked by Erickson) 应用数学作业代写
One of the most basic experiments in a physics laboratory is interferometry. It typically consists of an array of mirrors arranged in such a way that to light beams will interfere, causing an interference pattern. The interference pattern contains information that can be used to deduce physics of the phenomenon under study. It is a very basic but versatile experimental setup that countless variations (different mirror setups or using electrons, neutrons, atoms, or even big molecules1 as the ‘source’) exists for equally many purposes. In this problem we will consider one of the simplest setup involving only five main ingredients: a light source, a beam splitter, mirrors, phase control and photodetectors. This is shown in Figure 1. The light source will be producing pulses with two possible polarizations states — horizontal and vertical polarization states |H) , |V ), analogous to the classical linear polarization in optics.应用数学作业代写
(a)A beam splitter (BS) is classically a material that splits a light beam into two parts with smaller amplitudes along two different paths (cf. Figure 1). If it is a 50/50 BS, the light is split into two equal amplitudes. Quantum mechanically, this will be a material that takes in an input light state and gives a superposition of polarization statesand 50/50 BS means the superposition has equal weight, e.
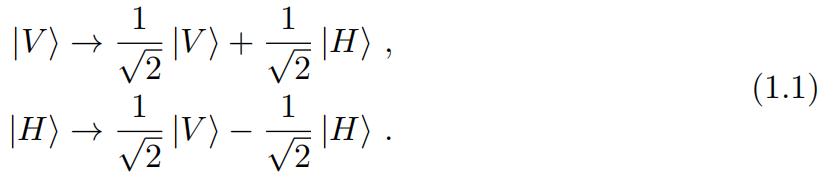
1People are ‘this’ close to do interferometry and double-slit experiments with small viruses!’
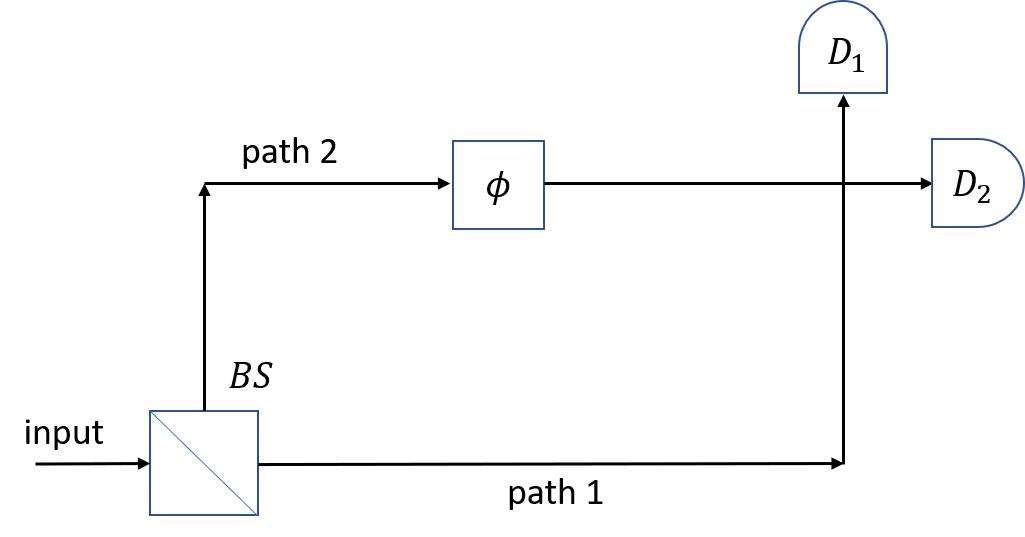
Figure 1: setup of the interferometer.
We can then label path 1 as the path where only vertically polarized light is allowed, and path 2 otherwise (i.e. the BS acts as a polarization filter2).
Find the matrix representation of the beam splitter operator3, denoted Bˆ, in the polarization basis {|V ) , |H)}. Show your working.
(b)In interferometry there is equipment that can adjust the phase of a light beam on one path. We call this equipment a phase control4(PC) which can add a phase φ
to a state. If the PC adds a phase φ to |H) and does nothing to |V ), find the matrix representation for the phase control operator C in this basis. Show your working.应用数学作业代写
(c)At the end we have two photodetectors D1, D2which are positioned in such a way that D1 will register a click if a photon arrives via path 1 and D2 if the photon arrives via path Let us assume as an approximation that those detectors carry out projective measurements. Find the matrix representation for the projection that D1 and D2 implement on |ψ).

(d)If the input state for the experiment is |V ), compute the output state right before the measurement is performed. 应用数学作业代写
What is the probability that D1and D2 registers aclick? Does the phase φ matter?
2Want to buy one? You can do it , e.g.,https://www.thorlabs.com/navigation.cfm?guide_id=2318.here I am not paid to say this.
3This gives a nice heuristic interpretation that in experiments we can actually think of lab equipment as operators that acts on the state.应用数学作业代写
4You can find them online too!https://www.thorlabs.com/NewGroupPage9.cfm?ObjectGroup_ID=711
(e)Nowwe consider a variation where just before the photodetectors, we insert another identical beam splitter (call it BS2) as in part (a), so the setup looks like Figure 2 below. Current technology allows us to insert this faster than the light-crossing time of the interferometer arms (before light reaches the end of the interferometer), so we can insert BS2 after we have sent the light pulse through BS15.
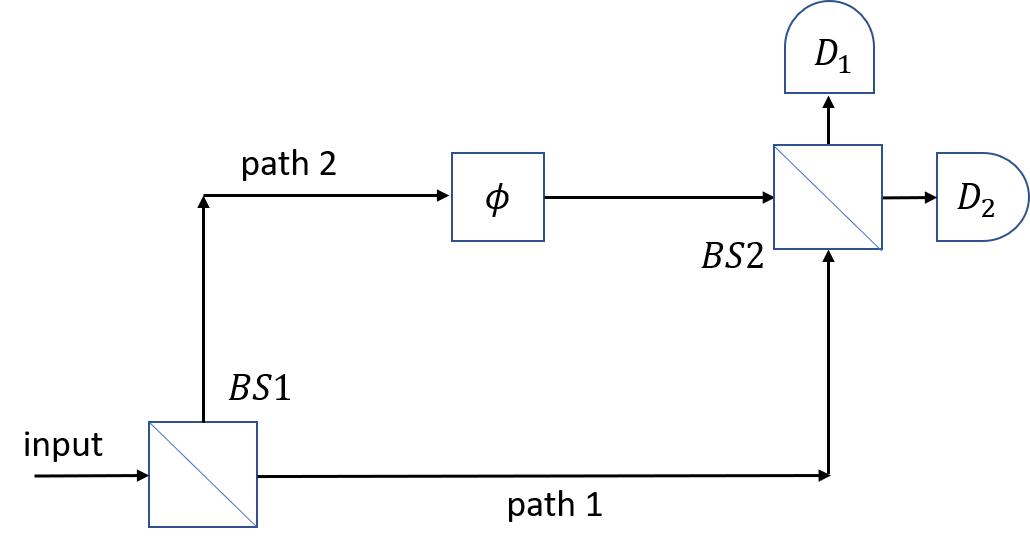
Figure 2: variation of the first interferometer which includes the second beam splitter BS2.
Compute the output state after BS2 and compute the probability that D1 registers a click.
What happens to the detection probability when φ = 0, π/2, π? Is the outcome of the experiment different from part (d)?
The source does not influence if the light behaves as a classical particle, or as a quantum entity that can go through both paths at the same time. It is indeed the experimental setup after the light is emitted that conditions how light behaves, and more concretely, whether we obtain information of which path the ‘photon’ goesMoral of the story: The light pulse was originated in the source, and only when it has already gone through the beam splitter, the extra beam splitter is introduced in part (e).应用数学作业代写
That means the light pulse (or the ‘photon’, if you insist on calling it that) could not have made the decision of which path to go in advance. In view of part (d) and part (e), it seems that the fact that light behaves as a particle (no interference, as in part (e), which means that only one detector clicks, the photon goes only on one path) or as a wavelike entity (interference pattern as in part (d), which means that both detectors click and the ‘photon’ is in a superposition of going through both paths) is experiment-dependent and completely independent of any decisions made at the source.
in our experiment. More on that on Block 3!
5This prevents the ‘photons’ from, for instance, know in advance whether they should make an interfer- ence pattern or not!
2 Stern-Gerlach again and again… (Marked by Richard)
In 1922 Otto Stern and Walter Gerlach experimentally verified the prediction of PeterDebye and Arnold Sommerfeld that electrons have an intrinsic6 angular momentum that is quantized. In Fig. 3 the experiment is shown. We consider a source that provides silver ions
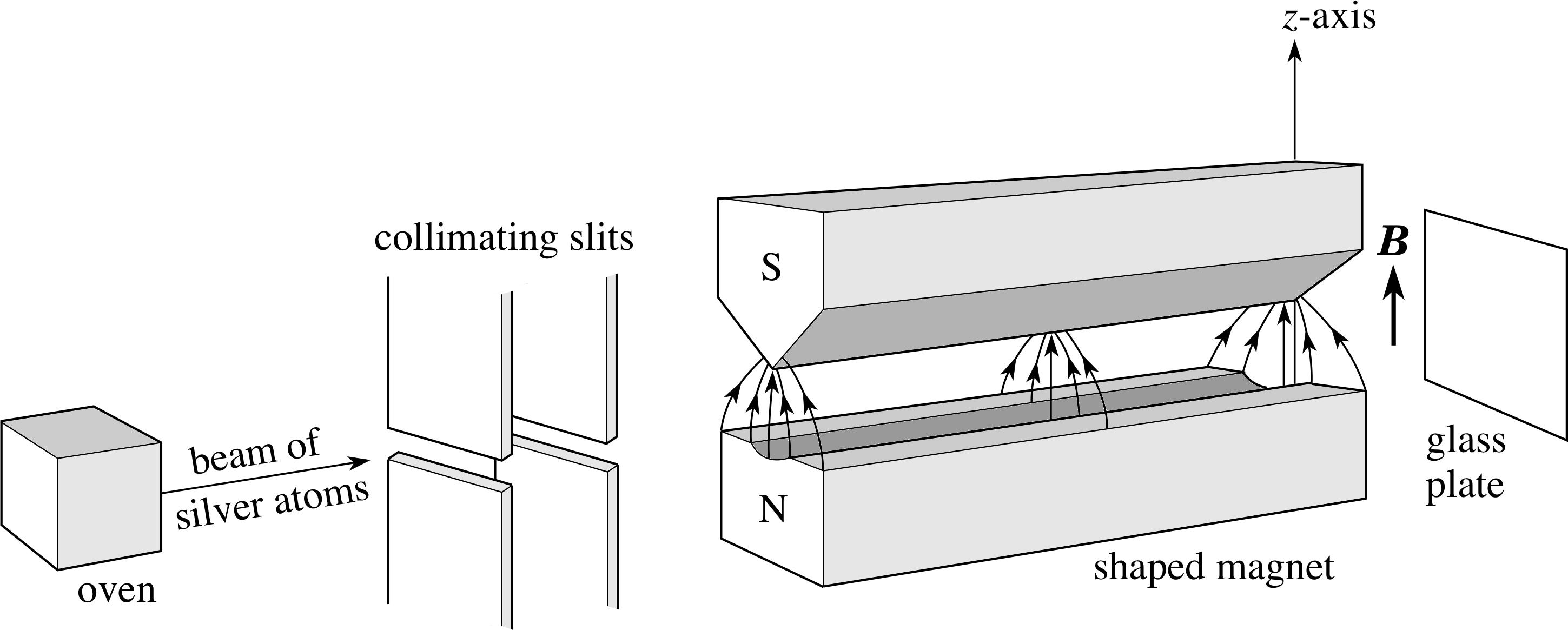
Figure 3: Experimental setup for the Stern-Gerlach experiment.
which are spin-1/2 particles, and assume that half of the atoms are prepared in the statecorresponding to the positive eigenvalue of the spin operator in the z direction sˆz = 1 σˆz,and the other half prepared in the state corresponding to the negative eigenvalue. Denotethe eigenstates by |±z). These atoms fly then through an inhomogeneous magnet where the magnetic field is along the z direction and the gradient of the field is parallel to that. The interaction potential of the atom and the field is Vˆ = −µˆ · Bˆ, where the magnetic moment of the atom is µˆ = gµBsˆ, g is the Land´e factor, µB is the Bohr magneton and sˆis the spin operator of the atom sˆ = (sˆx, sˆy, sˆz).应用数学作业代写
(a)If the force experienced by the atoms of the beam is proportional to the gradientof the interaction potential Fˆ = −∇Vˆ ,
show that the interaction results in a spatial splitting of the two different preparations of the atoms.应用数学作业代写
(b)Assume now that the atoms with negative spin in the z-component after the first magnet are discarded. This is equivalent to doing a projective measurement on the z-directionofspin on the remaining beam, with its corresponding update Now let the remaining beam of atoms go through a second magnet which is aligned in the x-direction. How many beams of atoms will appear on the glass plate gathering the results of the experiment? Relate your answer with the fact that the atoms cannot be simultaneously in an x and z eigenstates of the corresponding spin operators.
6Different from the orbital angular momentum Xˆ × Pˆ.
(c)What is the expectation value and variance of sˆx for the ensemble of atoms in the state |z) after the first magnet?
(d)Now assume again that after the second magnet the atoms with negative spin in sˆx are The other atoms go through a third magnet aligned along an arbitrary direction given by the unit spatial vector n which forms an angle θ with the z axis and an angle φ with the x axis (the usual co-latutide and azimuthal angles in spherical coordinates). What is the spin operator sˆn that this third splitter would be measuring (represented in the eigenbasis of sˆz)?应用数学作业代写
(e)Whatare the eigenstates of sˆn in the eigenbasis of sˆz?
(f)Calculate the probabilities that an atom after the second magnet is found in the eigenstate corresponding to the positive and negative eigenvalues of sˆn (spin up ordown with respect to the n direction). Particularize your result for the special cases:
(a)θ = 0, φ = π,
(b) φ = 0, θ =π/2,
(c) θ, φ = π/2.
3 Quantum Guess Who? (Marked by Pipo) 应用数学作业代写
Consider that you are given a qubit, that is, a two-level quantum system i.e the Hilbert space is two-dimensional. Let {|0) , |1)} be a basis of the qubit Hilbert space. The person who has given you the qubit tells you that they do not remember the state of the system,but they recall that it was either
- |ψ)1= |0) or
- |ψ)2= (|0) + |1))/√2
Since you go around claiming that you are a physicist, the person asks for your help.
(a)First,you wonder whether to perform a projective measurement in the {|0) , |1)} basis of the qubit would do the job. Compute the probabilities of getting each result, 0 or1, and explain if you can distinguish unambiguously the state you were given, either |ψ)1 or |ψ)2 by doing this kind of projective measurement. Notice that you can only distinguish the state unambiguously if for both options there is an outcome of your measurement such that you can be sure that the state was either one or the other.应用数学作业代写
(b)Now consider the following POVMelements:
√2
- Eˆ1= √ |1)(1|
1 + 2
√2
- Eˆ2= √ (|0) − |1))((0| − (1|)/2
1 + 2
- Eˆ3= 1 − Eˆ1 − Eˆ2
Discuss if with this set of measurements you can distinguish the state. Take into account that some outcomes from the measurement can be inconclusive, but never leading to a mistake.
4 Further ranting on PVMs (marked by Pipo) 应用数学作业代写
In this exercise you will analyze in detail one of the numerous problems related to measuringschemes involving projector valued measures (PVM). More concretely, we will analyze theinterplay between Heisenberg’s uncertainty principle and the fairy tale called “wavefunction collapse7”.
Consider a free quantum-mechanical particle in one dimensional space. The Hilbert space associated with this physical system is L2(R). Consider also the following family of projectors

where Ω is a subset8 of R. Note that the projector on the whole real line is identity: ΠˆR = 1and that if A and B are two disjoint subsets of R, i.e. A ∩ B = ∅, then ΠˆA∪B = ΠˆA + ΠˆB . Clearly, these projectors define a probability distribution in the sense that you were told in previous courses, that is, one can always define the probability of a particle in astate |ψ) to be in a region Ω with Born’s rule
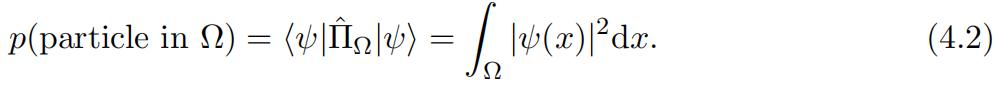
Since this is a projective measurement, we now the update rule: if you find the particle somewhere it will remain in that somewhere right? Or in other words, the state after the measurement should then be given by but this leads to some problems, as we will see.

7One of the less cruel German fairy tales, unlike H¨ansel and Gretel or the Sleeping Beauty (for reference check the original stories)
8e.g., an interval.
4.1 Part I: Oops, there is a problem with this.
(a)Show that the new wave function in the position representation, i.e. (x|ψj) = ψj(x), is of theform
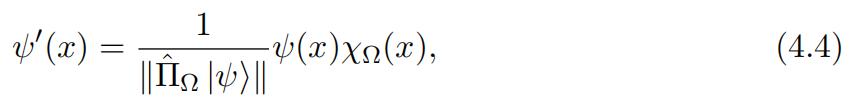
where
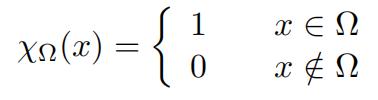
(b)Calculatethe variance (uncertainty squared) of the momentum operator Pˆ, e. ∆2 ,P ie.in the new state |ψj). Consider states not initially moving on average for simplicity, that is, (ψ|Pˆ|ψ) = 0. Also, consider Ω to be an arbitrary interval (a, b). Will the new state |ψj) always be in the domain of the momentum operator provided that |ψ) was?
4.2 Part II: Wait, maybe we can fix it?
One could think that the problem appearing in previous part is somehow related to the sharpness of the measurement, that is, that the projectors defined by equation (4.1) con- strain too much the information about that system to have a smooth notion of “state update”. Therefore, one could perhaps expect to be able to find a set of better behaved projectors.
Indeed, consider a set of functions defined by taking a smooth, compactly supported9 function ψ0(x) and modulating with a phase and translating it along the real line, i.e.
(x|ψm,n) = ψm,n(x) = ei2πmxψ0(x − n), (4.5) 应用数学作业代写
where m, n ∈ Z. Perhaps these functions span all possible states of the system by linearcombination (i.e., ny wavefunction may be written as a combination of them). Further, theoverlap of an arbitrary state with this set of functions (their inner product) should give anapproximate localization of the particle in the real line, provided that the function ψ0(x) issupported around zero. Pictorially You can imagine ψ0(x) as some sort of smooth window function that decays away from the origin, adding the translation displaces that window, so we have a set of window functions covering the whole space.
So! do we have a nice basis to project on that is localize in space?
As we will see, we are not required to give an explicit expression for ψ0(x) to check that, even in this case, the problem persists.
9Compactly supported: The support if the function is compact. In other words, for a real function, the function is closed and bounded (is zero everywhere except it is finite for a finite set of intervals).
For the set of |ψn,m) to give a reasonable measuring scheme, i.e. to assign probabilities, we require it to be an orthogonal basis of the Hilbert space, in such a way that

Moreover, in order to avoid the problem of part I we also require that each |ψn,m) belongs to the domain of both the momentum and the position operators, in such a way that we can measure the position and the momentum of the particle consecutively according to the update rule

where

You are asked10 to prove that these two requirements are incompatible by answering the following questions.
The way to proceed is to assume that |ψ0) belongs to the domainsof both position and momentum, and that the set of functions |ψm,n) generated by it forms a basis. This will lead to a contradiction.
(a)Consider the vectors Xˆ |ψ0) and Pˆ |ψ0), by assumption they belong to the Hilbert Show that
(ψ0|Xˆ|ψm,n) = (ψ−m,−n|Xˆ|ψ0) (4.9)
and that
(ψ0|Pˆ|ψm,n) = (ψ−m,−n|Pˆ|ψ0) (4.10) 应用数学作业代写
(b)By assuming the completeness relation of the set |ψm,n), i.e. equation (4.6), show that
(ψ0|XˆPˆ|ψ0) = (ψ0|PˆXˆ|ψ0) . (4.11)
(c)Finally, reach a contradiction (it’s an obvious..).
10In case there is any doubt after so much text, you need to answer only a), b) and c). Anything before that is for you to read and understand.

其他代写:代写CS C++代写 java代写 matlab代写 web代写 作业代写 物理代写 数学代写 考试助攻 paper代写 金融经济统计代写
