年金终值就是在已知等额收付款金额Present、利率（这里我们默认为年利率）interest和计息期数n时，思量钱币的时间代价，计较出的这些收付款到到期时的等价票面金额。
而年金按其每次收付产生的时点（即收付当日日是在①有限期的首期期末、②有限期的首期期初、③有限期的若干期后的期末、④无限期）的差异，可分为：普通年金（后付年金）、先付年金、递延年金、永续年金等几种，故年金终值亦可分为：普通年金终值、先付年金终值、递延年金终值。（注：永续年金只有现值，不存在终值。）
分类与计较编辑普通年金终值
普通年金终值：指一按时期内，每期期末等额收入或支出的本利和，也就是将每一期的金额，按复利换算到最后一期期末的终值，然后加总，就是该年金终值。譬喻：每年存款10000元，年利率为10%，颠末5年，逐年的终值为年金终值，计较为：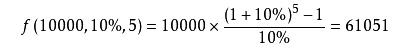
记作F=A（F/A，i，n）。推导如下：
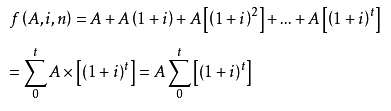
假如年金的期数n许多，用上述要领计较终值显然相当繁琐。由于每年付出额相等，折算终值的系数又是有纪律的，所以，可找出轻便的计较要领，其思路为：将其视为以（1+i）为公比的等比数列，回收等比数列求和公式，将其简化为以下公式：
设每年的付出金额为A，利率为i，期数为n，则按复利计较的年金终值F为：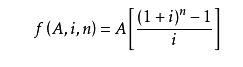
式中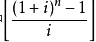
为普通年金终值系数后付年金终值系数，利率为i，颠末n期的年金终值记作(F/A，i，n)，可查普通年金终值系数表。
先付年金终值
先付年金终值：是其最后一期期末时的本利和，相当于各期期初等额收付金钱的复利终值之和。
n期先付年金与n期普通年金的收付款次数沟通，但由于付款时间差异，n期先付年金终值比n期普通年金的终值多计较一期利钱。因此在n期普通年金终值的基本上乘以（1+i）就得出n期先付年金的终值了，公式为：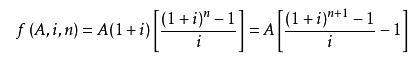
记作F=A·[(F/A，i，n+1)-1]
则假如上例为每年头计息的话，颠末5年，逐年的终值为年金终值，计较为：
以上应改为=10000×﹛[﹙1+10%）^6-1]÷10%-1﹜=67156.1
