CVEN2002
Part A: Numerical Methods
常微分方程代写 Question 1 (20 marks)Consider an Exponential distribution, that is the probability distribution of the time between events in a ···
Question 1 (20 marks) 常微分方程代写
Consider an Exponential distribution, that is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. The probability density function of the Exponential distribution is expressed as the following
p(x) = λe-λx
Assume that the rate parameter of the distribution is λ = 1.5.
Numerically compute p(0 < x < 4).
(a) [5 marks] Apply single application trapezoidal rule.
(b) [5 marks] Apply multiple-application trapezoidal rule with n = 4.
(c) [5 marks] Apply multiple-application trapezoidal rule with n = 8.
(d) [5 marks] Calculate the relative error for (a), (b) and (c) given the exact solution is 0.9975. Also, show that the relative error is roughly inversely proportional to n .
NOTE: Round to 6 decimal points when necessary.Term 2, 2019
Question 2 (20 marks) 常微分方程代写
We have the following ordinary differential equation (ODE)
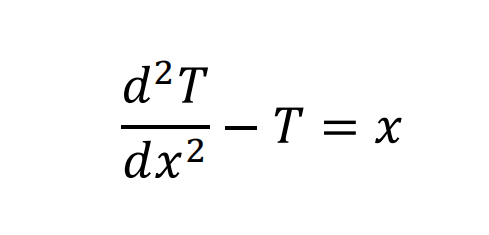
(a) [3 marks] Convert the above ODE into a system of first-order ODEs.
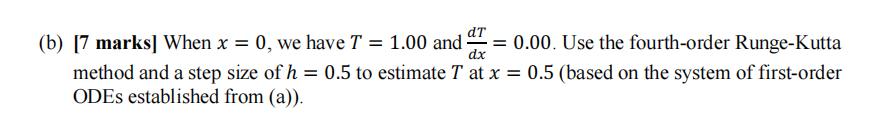
(c) [10 marks] When x = 0, we have T = 1.00; when x = 1.5, we have T = 2.981689. Use Finite-Difference Method and a step size of ∆x = 0.5 to estimate T for x = 0.5 and x = 1.0.
NOTE: Round to 6 decimal points when necessary.

其他代写:英国代写 homework代写 program代写 project代写 assignment代写 加拿大代写 python代写 report代写 paper代写 essay作业代写 作业代写 北美作业代写 java代写 matlab代写 finance代写
