Econ304 Quantitative Macroeconomic Theory
Midterm
定量宏观经济理论代写 Part II Essay Questions 40 points Give a clear and complete explanation of your answers. Keep the answers simple and to the point.
Part II Essay Questions 40 points
Give a clear and complete explanation of your answers.
Keep the answers simple and to the point.
If you need to make any assumptions, state them clearly.
1.(18 + 3 extra points) 定量宏观经济理论代写
Suppose Isabel divides her life into two periods, period 1 and period 2. She earns Y1in period 1 and Y2 in period 2 and pays lump-sum taxes, T1 in period 1 and T2 in period 2, to the We assume that Y2 – T2; Y1 – T1 > 0. She can borrow or lend between period 1 and period 2 at the real interest rate r. Her lifetime utility is defined as U(C1; C2) = u (C1) + βu (C2) over consumption in period 1, C1, and in period 2, C2; where β > 0. The momentary utility is of the form
u (C) = log C
Isabel allocates her resources across both periods consumption according to the optimality condition
uC (C1) = (1 + r) βuC (C2)
(a) (4 points) Write Isabel’s first period and second period budget constraints and use them to derive her intertemporal budget constraint.

(c) (2 points) Suppose Isabel’s income in period 2 went up. Use your answers to the previous question to show what will happen to her consumption in each period of her life and her first period saving?
(d) (2 points) Suppose the interest rate rises, what will happen to Isabel’s consumption in each period of her life and first period savings?
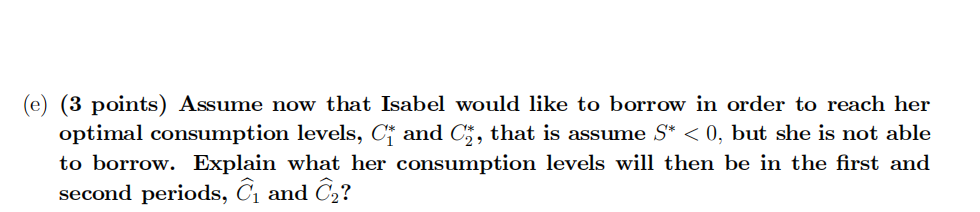
(f) The government wants to set up a tax-transfer program to help households like Isabel. It levies a lump-sum tax on households in each period, T1 and T2, with a negative lump-sum tax being equivalent to a lump-sum transfer. The government can borrow or lend at the market interest rate r and has no expenditures on goods or services in either period.
i. (3 points) Write the government intertemporal budget constraint.

2.(12 points + 4 extra points) 定量宏观经济理论代写
Consider an economy where two types of households, household A and household B, live for 2 periods, and receive identical endowments of income (Y1; Y2) in the first and second period respectively. Their lifetime utility is defined as U(Ci;1; Ci;2) = u (Ci;1) + βiu (Ci;2) over consumption in period 1, Ci;1, and in period 2, Ci;2; for i = A; B where βA> βB> 0.
Both household types allocate their resources across both periods consumption according to the optimality condition
uC (Ci;1) = (1 + r) βiuC (Ci;2) for i = A; B
where r is the real interest rate at which they can borrow or lend. The momentary utility is of the form
u (C) = log C

(b) (3 points) Define the competitive equilibrium for this endowment economy.
(c) (5 points) Solve for the equilibrium gross real interest rate, 1 + r.
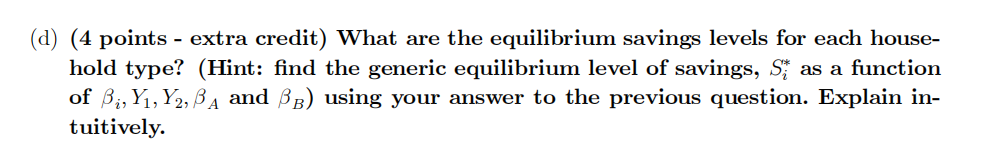
3.(10 points) 定量宏观经济理论代写
Consider a two-period economy where the representative firm uses a production technology given by Yi= ziF (Ki; Ni) for i = 1; 2, where Ki is the capital input, that depreciates at the rate δ , and Ni is the labor input used by the firm in period i to produce Yi.
Suppose that in period i, for i = 1; 2, the government levies a proportional tax, ti ; where ti ∈ (0; 1) on firms revenue Yi . So the taxes paid by the representative firm are tiYi . The tax revenues are rebated lump-sum to households. Let T Ri denote the lump sum transfer that the representative consumer receives.
The representative firm owns capital, pays a wage rate w per unit of labor hired and can borrow or lend at the market real interest rate r. It decides on how much labor to hire in each period and how much capital to accumulate for the following period in order to maximize the present discounted value of after-tax profits:

(b) (2 points) How do the tax rates impact on capital accumulation and each period’s output. Explain the different impact of t1 and t2 .
(c) (4 points) Assume δ = 1 and solve for the equilibrium level of capital accumulation and output.

