ECON 711 Macroeconomic Theory and Policy
宏观经济作业代写 Derive optimality conditions that characterize the solution to the planner’s problem.Give intuition for those optimality conditions.
Problem Set 2 宏观经济作业代写
Module 2-1: The Neoclassical Growth Model in Discrete Time
1.Ramsey-Cass-Koopmans model. model. Suppose the planner seeks to maximize the intertemporal utility function
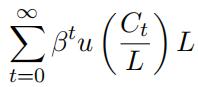
subject to the sequence of resource constraints
Ct + Kt+1 = F(Kt , AL) + (1 − δ)Kt , 0 < δ < 1
given initial K0 > 0. Suppose for simplicity that the labor force L and the level of productivity A are constant. Let ct , kt , yt etc. denote consumption, capital, output etc in per worker units. Suppose that the period utility function and the production function have their usual properties.
(a) Derive optimality conditions that characterize the solution to the planner’s problem.Give intuition for those optimality conditions. Explain how these optimality conditions pin down the dynamics of ct and kt. 宏观经济作业代写
(b) Now suppose that the production function is Cobb-Douglas, Y = F(K, AL) = Kα(AL) 1−α with 0 < α < 1. Derive expressions for the steady state values k ∗ , y∗ , c∗ in this economy. How do these steady state values depend on the period utility function? Explain.
(c) What is the steady state savings rate in this economy? Explain how the steady state savings rate depends on the parameters α, β, δ and the level of productivity A. Give intuition for your answers.
(d) Suppose the economy is initially in the steady state you found in (b). Suppose the economy becomes more patient with the discount factor increasing from β to β 0 > β. Use a phase diagram to explain (i) how this change affffects the long-run values of consumption,capital and output, and (ii) how the economy transitions to these new long-run values. How would your answers diffffer if the discount factor fell from β to β 0 < β. ?

2.Isoelastic utility function. Consider the utility function 宏观经济作业代写
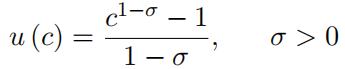
(a) Show that u(c) is strictly increasing and strictly concave.
(b) Show that the relative curvature of the utility function
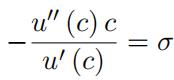
is independent of the level of consumption.
(c) Consider the case σ = 1. Show that this corresponds to u(c) = log c. [Hint : what is the antiderivative of c −1 ?]

更多代写:美国Accountant会计网课全包 gmat远程代考 美国代考网课 出国留学文书代写 传播学论文代写 证券投资分析代写
