Multi-Agent Systems
Final Homework Assignment
多代理系统代写 IMPORTANT This project is an individual assignment. So everyone should handin their own copy. The questions below require programming.
IMPORTANT
- This project is an individual assignment. So everyone should handin their own copy.
- The questions below require programming. In addition to the report (addressing the questions and discussing the results of yourexperiments), also provide the code on which yourresults are based (e.g. as Python notebooks). However, make sure that the report is self-contained, i.e. that it can be read and understood without the need to refer to the code.
- Store the pdf-report and the code in a zipped folder that you upload via canvas. Use your name and VU ID as name for the zipped folder, e.g.
John_Doe_1234567.zip
- This assignment will be graded. The max score is 4 and will counttowards your final grade.
- Your final grade (on 10) will be computed as follows:
Assignments 1 thru 5 (max 1) + Individual assignment (max 4) + Final exam (max 5)
1 Monte Carlo estimation of Shapley value (25%) 多代理系统代写
Consider n agents (A, B, C . . . N) boarding a (sufficiently large) taxi at location 0 on the real line. They share the taxi to return home. Agent A lives at distance 1, B at distance 2, etc. In general, for agent ai the distance to home equals i. The taxi driver agrees that they only need to pay the fare to the most remote destination (which is at location n).
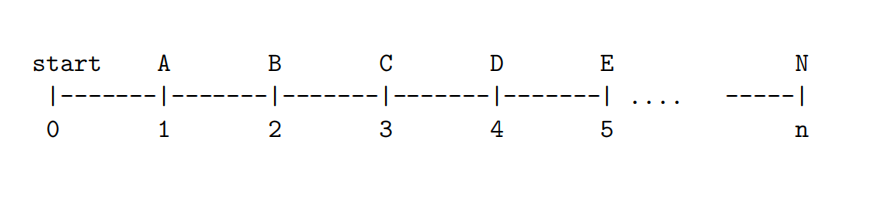
Questions
- Compute (using the theory) the Shapley values for this problem when n is small, e.g. n = 4 or 5. This will allow you to generalise to arbitrary values of n.
- Now set n to a large value, e.g n = 50 or n = 100. From the above you are able to guess what the Shapley values will be. However, use Monte Carlo sampling to find an approximate value for the Shapley values in this case. Discuss how effective Monte Carlo sampling is for this problem.
2 Monte Carlo Tree Search (MCTS) (25%) 多代理系统代写
Construct binary tree
Construct a binary tree of depth d = 20 (or more – if you’re feeling lucky). Since the tree is binary, there are two branches (aka. edges, directions, decisions, etc) emanating from each node, each branch (call them L(eft) and R(ight)) pointing to a unique child node (except, of course, for the leaf nodes – see Fig 1). We can therefore assign to each node a unique “address” (A) that captures the route down the tree to reach that node (e.g. A = LLRL – for an example, again see Fig 1). Finally, pick a random leaf-node as your target node and let’s denote its address as At .
Assign values to leaf-nodes
Next, assign to each of the 2d leaf-nodes a value as follows:
- For every leaf-node i compute the edit-distance between its address Aiand the address Atof the target leaf, i.e. di := d(Ai , At).
- Recall that the edit-distance counts the number of positions at which two strings differ, e.g.:
d(LRLR, LRRR) = 1, d(LRRL, LLLL) = 2, d(RRLL, RLRR) = 3
- Finally, define the value xiof leaf-node i to be a decreasing function of the distance di= d(Ai , At) to the target node, and sprinkle a bit of noise for good measure: e.g. 多代理系统代写
xi = Be−di/τ + εi
where B and τ are chosen such that most nodes have a non-negligible value (e.g. B = 10 and τ = dmax/5 and εi ∼ N(0, 1) ).
Questions
- Implement the MCTS algorithm and apply it to the above tree to searchfor the optimal (i.e. highest) value.
- Collect statistics on the performance and discuss the role of the hyperparameter c in the UCB-score.
Assume that the number MCTS-iterations starting in a specific root node is limited (e.g. to 10 or 50). Make a similar assumption for the number of roll-outs starting in a particular (”snowcap”) leaf node (e.g. 1 or 5).
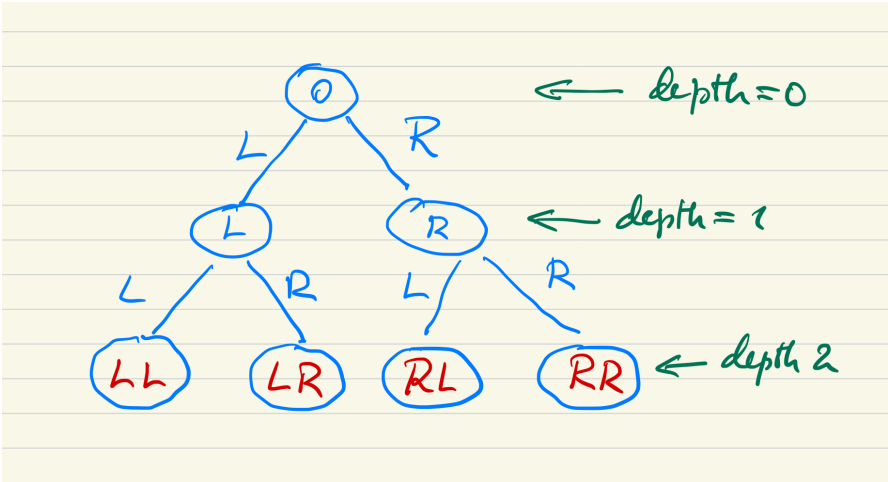
Figure 1: Example of binary tree of depth 2. The “address” of the leaf-nodes (layer 2) is indicated in red.
3 Reinforcement Learning: SARSA and Q-Learning for Gridworld (50%) 多代理系统代写
Consider the 9 × 9 gridworld example depicted in the figure 2 below. The blue gridcells represent walls that cannot be traversed. The green cell represent a treasure and transition to this cell yields a reward of +50 whereupon the episode is terminated (i.e. absorbing state). The red cell represents the snakepit: this state is also absorbing and entering it yields a negative reward of −50. All other cells represent regular states that are accessible to the agent. In each cell, the agent can take four actions: move north, east, south or wes (not moving is NOT a valid action). These actions result in a deterministic transition to the corresponding neighbouring cell. An action that makes the agent bump into a wall or the grid-borders, leaves its state unchanged. All non-terminal transitions (including running into walls or grid borders) incur a negative reward (”cost”) of −1.
For the questions below, we assume that the agent is not aware of all the above information and needs to discover it by interacting with the environment (i.e. model-free setting).
Questions 多代理系统代写
Perform, compare and comment on, the following experiments:
- Use SARSA in combination with greedification to search for an optimalpolicy.
- Use Q-learning to search for an optimal policy. Implement two different update strategies:
(a) Direct updates: Update the Q-table while rolling out each sample path;
(b) Replay buffer: Collect the experiences (s, a, r, s′ ) in a replay buffer and sample from this buffer.
Compare the solutions and the corresponding computational effort for the three solution strategies.
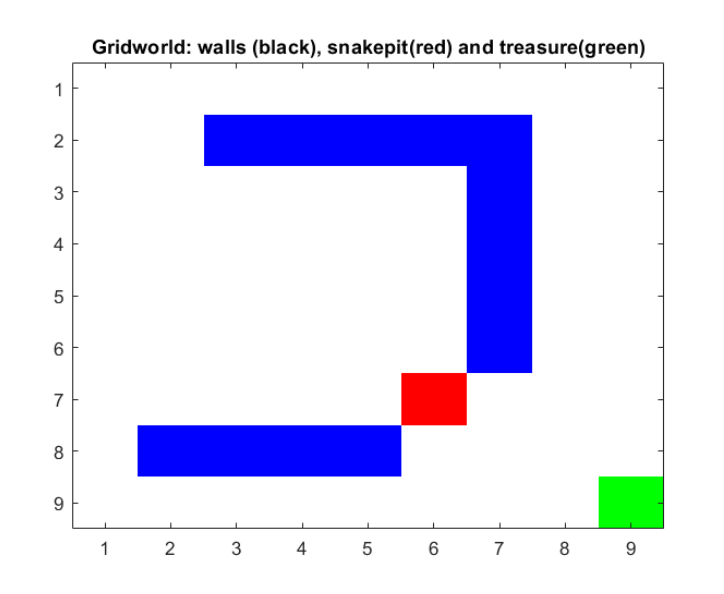
Figure 2: Gridworld 9 × 9: walls (blue), treasure (green) and snakepit (red).

