CS 381-Fall 2020
Name:
Date: November 11, 2020
基本图算法作业代写 LO 1.4 Students are able to extend the ideas behind fundamental graph algorithms like DFS, Dijkstra, Bellman-Ford to develop
Homework 5
Due Date: November 17, 2020 at 11:59PM on Gradescope.
Instructors: Jeremiah Blocki and Elena Grigorescu
Learning Objectives 基本图算法作业代写
The homework is relevant to the following learning objectives:
- LO 1.4 Students are able to extend the ideas behind fundamental graph algorithms like DFS, Dijkstra, Bellman-Ford to develop their own graph algorithms.
- LO 1.5 Students are able to use the network flow problem to solve appropriate algorithmic problems e.g., by reducing problems like bipartite matching, baseball elimination to network flow.
- LO 2.5 Students are able to analyze the complexity of algorithms which use funda- mental graph algorithms (e.g., Dijkstra, Bellman-Ford, DFS, BFS, Network Flow) as a building block.
- LO 3.4 Students can provide correctness proofs for fundamental graph algorithms like 基本图算法作业代写
Dijkstra, Kruskal, Kosaraju and Prim’s MST algorithm and are able to generalize these ideas to prove that related graph algorithms are correct
- LO 3.5 Students are able to find a min-cut given the maximum-flow and vice versa and interpret the min-cut (resp. max-flow) as a certificate of optimality for the max-flow (res. min-cut). Students can use the max-flow min-cut theorem and residual graphs to reason about the correctness of a network flow algorithm like Ford-Fulkerson.
- L0 3.6 When reducing a problem (e.g., bipartite matching) to network flow students are able to show that the reduction is correct and explain how to use the network flow solution to extract the solution to the original problem.
Homework Guideline Reminders 基本图算法作业代写
Assignments must be typed. Submit one pdf file to Gradescope by 11:59PM, or else late penalties will apply. The pdf file can include hand-drawn images of figures.
Each question needs to include a resources and collaborator (RC) statement. You will not be penalized for using resources or having collaborators if your answers are expressed in your own words. If you consulted no resources outside of course material or had no collaborators, you must state so. A question without a complete RC statement will not be graded.基本图算法作业代写
Question 1 (25 points)
Let G = (V, E) be a graph with n nodes and m edges with weights w(e) on the edges. Suppose we have already computed the minimum spanning tree T of G. Develop an efficient algorithm to update T in the following circumstances:
(a)We add a new node vjto G and connect vj to each node v ∈ V with weight w(vj, v).
(b)We delete an edge e fromG.基本图算法作业代写
(c)Weadd 100 new edges e1, . . . , e100 with weights w(e1), . . . , w(e100).
(d)We find anode v V with degree 3 and remove v from G. You may assume that G v is still connected.
You should analyze the running time of your algorithm and give a brief, but precise, proof that the new tree T j is the minimum spanning tree for the new graph Gj. For full credit your algorithms should be as efficient as possible. In part A your algorithm must run in time O(n log n). You may assume that all edge weights are distinct before and after the updates and that all graphs are input in adjacency list representation.
Solution:
Resources:
Collaborators:
Question 2 (25 points)
Consider the following flow network such that the initial flow was empty. We executed the Ford-Fulkerson algorithm described in class until the flow shown below was obtained. The notation x/y on edge e indicates that the current flow on edge e is 8 and the capacity of the edge is c(e) = y e.g., the current flow on the edge e = (a, d) is 8 and c(a, d) = 15. To answer the following questions, you may include photographs of hand-drawn graphs or designed by tikz package in latex.基本图算法作业代写
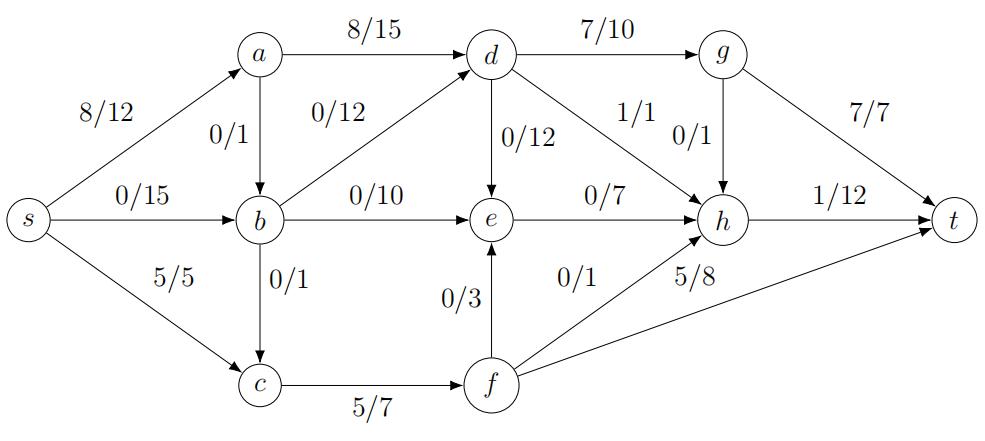
(a)What is the value of the current flow f ? Briefly justify your answer. (2 points)
(b)Drawthe residual graph for this flow network and show an augmenting path on (5 points)基本图算法作业代写
(c)Continue the Ford-Fulkerson algorithm and determine the sequence of paths inresidual graph which maximize the number of augmentation steps. (Just write the name of paths according the nodes included in the path). (10 points)
(d)Drawthe flow that you obtained from part C What is the value of the max-flow f ? (4 points)
(e)What is the minimum s-t cut? Explain how you arrived at your answer. (4points)
Solution:
Resources:
Collaborators:
Question 3 (25 points) Flu Shot Drive
A local organization enlists the help of Purdue Pharmacy and PUSH to organize a flu shot drive. Due to COVID-19 restrictions, this flu shot drive requires some careful planning and thus they seek the help of CS381 students as well.基本图算法作业代写
The local organization has an online sign-up form where each family can sign up for one time slot in which all the family members will be administered their flu shots. Suppose d different families have signed up for the drive in advance, and each family needs to be assigned to one of r rooms during one of t different time slots to have their flu shot administered. At most one family’s flu shot can be scheduled in each room during each time slot.Conversely, families cannot be split into multiple rooms/times. Moreover, each of these flu shot administrations must be supervised by one of n nurses. Each nurse can supervise at most one family’s flu shot administration at a time. Each nurse is available for certain timeslots, and no nurse can supervise more than 10 family flu shot administrations in total.基本图算法作业代写
Formally, the input to your algorithm is the following:
- Integer array D[1 . . .d], where D[i] is the number of members in the ith family.
- Integer array R[1 . . . r], where R[j] is the number of seats in the jth ro The ith family can be assigned to the jth room if and only if D[i] ≤ R[j].
- 2-Darray S[1 . . . t, 1 . . . n] only containing values 0, 1 , where S[p, q] = 1 if and only if the qth nurse is available during the pth time slot.基本图算法作业代写
Let N := d + r + tn be the total size of your input.
- Design and analyze an algorithm that schedules a room, a time slot, and a nurse for every family’s flu shot administration, or reports that no such schedule is possible.
- Argue your algorithm’s correctness.
Solution:
Resources:
Collaborators:
Question 4 (25 points) Food delivery 基本图算法作业代写
Jack is a food delivery person and he is going to deliver the last round of food from the restaurant to customers’ homes. He will go directly to his own home after finishing this round of delivering. There are n 2 customers waiting for food at their homes and Jack has the map of the city. On the map, every road is a one-way road and there is no cycles among these roads. Jack learned algorithms and he immediately notices that the restaurant,customers’ homes, his own home, and those roads compose a directed acyclic graph G(V, E) ( E = m, V = n). The restaurant s and his own home t is the unique source and sink vertex of this graph. He is in the restaurant at the beginning.基本图算法作业代写
- Can you describe an algorithm to help Jack determine whether he can deliver every customers’food and go to his own home? Give the algorithm, proof of correctness and running
Hint: This question is equivalent to determining whether G has a Hamiltonian path.
(A Hamiltonian path in G is a directed path that contains every vertex in G)
- Eachcustomer vi will give some tips T [vi](T [vi] > 0) to the delivery The tips varies from customer to customer and are already known. Jack just found that his car could only go another l(l < n) miles and each road in the city (i.e. edges in G) has a length of one mile, please design and analyze an efficient algorithm to help Jack find the a path home that maximizes his tips. You may assume there is a feasible path of length at most l. (Jack doesn’t need to deliver all customers’ food, but can only get tips from those he delivers. He has to get home in the end.)基本图算法作业代写
Solution:
Resources:
Collaborators:

