On a generalization of the Hadwiger-Nelson problem
Hadwiger-Nelson problem代写 For a field F and a quadratic form Q defined on an n-dimensional vector space V over F , let QGQ, called the
Mohammad Bardestani, Keivan Mallahi-Karai October 15, 2018
Abstract Hadwiger-Nelson problem代写
For a field F and a quadratic form Q defined on an n-dimensional vector space V over F , let QGQ, called the quadratic graph associated to Q, be the graph with the vertex set V where vertices u, w V form an edge if and only if Q(v w) = 1. Quadratic graphs can be viewed as natural generalizations of the unit-distance graph featuring in the famous Hadwiger-Nelson problem.
In the present paper, we will prove that for a local field F of characteristic zero, the Borel chromatic number of QGQ is infinite if and only if Q represents zero non-trivially over F . The proof employs a recent spectral bound for the Borel chromatic number of Cayley graphs, combined with an analysis of certain oscillatory integrals over local fields. As an application, we will also answer a variant of question 525 proposed in the 22nd British Combinatorics Conference 2009 [6].
1 Introduction
The celebrated Hadwiger-Nelson problem asks for the minimum number of colors required to color Rn such that no two points at distance one from each other have the same color. Recall that the chromatic number of a graph G, denoted by χ(G), is the least cardinal c such that the vertices of G canbe partitioned into c sets (called color classes) such that no color class contains an edge in G. Hadwiger-Nelson problem代写
Hence,the Hadwiger-Nelson problem is the question of finding χ(Gn), where Gn is the graph with vertex setV (Gn) = Rn, where the adjacency of vertices x, y ∈ V (Gn) is defined by the equation Q(x − y) = 1;here, Q(x1, . . . , xn) = x2 + · · · + x2 is the canonical positive-definite quadratic form on Rn. Although1 nit is not hard to show that
(1) 4 ≤ χ(G2) ≤ 7,
the question of determining the exact value of χ(G2) remains an open problem to date. For a discussion of historical developments on this problem and its extension to χ(Gn) we refer the reader to [15, 19].
The definition of chromatic number allows the color classes to be arbitrary subsets of the vertexset. When the vertex set is equipped with an additional structure (e.g., a topology, or a σ-algebra structure), one can define a variant of the chromatic number by imposing further constraints on thecolor classes related to this structure. The Borel chromatic number of a topological graph G, denoted by χBor (G), is the least cardinal c such that the set V (G) can be partitioned into c Borel subsets none of which contains two adjacent vertices of G.Hadwiger-Nelson problem代写
Once the Borel measurability assumption is imposed on the color classes,
a wide range of analytical tools will become available, in order to establishbounds on the Borel chromatic number of the graphs in question. One of the pioneering papers in this direction is the work of Falconer [8] who proved that under the measurability assumption onecan improve (1) to give χBor (G2) ≥ 5. These techniques have been further developed by Bukh [5], Bachoc–Nebe–Oliveira–Vallentin [4] and Oliveira–Vallentin [7].
The main question addressed in this paper concerns a new generalization of the Hadwiger-Nelson problem. Let F be an arbitrary field of characteristic different from 2, and let V be a finite-dimensional vector space over F . Given a non-degenerate quadratic form Q defined on V , we will use the term
Keywords: Hadwiger-Nelson problem代写
Bessel function; Chromatic number; Fourier transform; Local fields.2010 Mathematics Subject Classification: Primary 05C90; Secondary 47A10.
quadratic space to refer to the pair Q = (V, Q). For a quadratic space Q = (V, Q), we can now define the quadratic graph QGQ as follows. The vertex set of QGQ coincides with the vector space V . Vectors v, w ∈ V are adjacent in QGQ if and only if Q(v − w) = 1. More succinctly, QGQ is the Cayley graph of the abelian group V with respect to the unit sphere S = {v ∈ V : Q(v) = 1}. Recall that a quadratic form Q defined over V is isotropic if there exists a non-zero vector v ∈ V with Q(v) = 0. Otherwise, Q is called anisotropic. The main result of this paper is the following:
Theorem 1.1.
Let F be a local field of characteristic zero, V a finite-dimensional F -vector space of dimension at least 2, and Q = (V, Q) the quadratic space associated to a non-degenerate quadraticform Q on V . Then χBor (QGQ) is finite if and only if Q is anisotropic.
A local field is, by definition, a topological field with a non-discrete locally compact topology. It is well-known that a local field of characteristic zero is isomorphic to the field of real or complex numbers, or to a finite extension of the field of p-adic numbers Qp, where p varies over the set of prime numbers.Hadwiger-Nelson problem代写
Theorem 1.1 shows in particular that whether or not the form Q is isotropic can be read off the Borel chromatic number of the associated quadratic graph. One can likewise inquire about thechromatic number of quadratic graphs over number fields. For the quadratic space Q = (Q2, x2 + y2), Woodall [21] has shown that χ(QGQ) = 2. Using the local-global principle, we can deduce a purely algebraic corollary of Theorem 1.1 that applies to the ordinary chromatic number of quadratic forms over number fields.
Corollary 1.2. Hadwiger-Nelson problem代写
Let K be a number field, V a finite-dimensional K-vector space of dimension at least2, and QK = (V, Q) the quadratic space associated to a non-degenerate quadratic form Q on V . If Qis anisotropic, then χ(QGQK ) is finite.Proof. By HasseMinkowski theorem, there exists a place ν of K such that the form Q(x) is anisotropic over the completion F = Kν . Since F is a local field, by Theorem 1.1, we have χBor (QGQF ) < ∞,where QF is the quadratic space on K defined by Q. Hence, a fortiori, χ(QGQK ) ≤ χ(QGQF ) ≤χBor (QGQF ) < ∞.
Let us describe the key ideas of the proof of Theorem 1.1.
For anisotropic forms, a partitioning of the space F n into box-like subsets, and periodically coloring these boxes yields a proper coloring. The main technical part of the work goes into the proof of the theorem for isotropic forms. Here we use a spectral bound established in [3] which provides a lower bound on the Borel chromatic number ofCayley graph of vector space V with respect to Borel measurable set S = {v ∈ V : Q(v) = 1}, which is analogous to the well-known Hoffman bound for finite graphs.
This bound,
per se, is only applicable when S is bounded, which is never the case here. Instead, we will approximate S by an increasing family {ST }T ≥1 of bounded Borel sets. The crucial step in the proof will consist of establishing a useful lower bounds for the a family of oscillatory real and p-adic integrals that arise as the Fourier transform of carefully chosen probability measures on {ST }. The latter is dealt with using van der Corput’s lemma in the real case and certain Bessel functions in the p-adic case.
In certain cases, one can attempt to quantify Theorem 1.1 for anisotropic forms. Let p > 2 be a prime number and set Qp = (Q2, x2 + x2). Note that if p ≡ 3 (mod 4), then the quadratic form x2 + x2 is anisotropic over Qp and hence χ (Qp) < ∞. Indeed, by keeping track of the bounds in the proof of Theorem 1.1 for anisotropic quadratic forms, one can see that χBor(QGQ ) = O(p2). Wecan now pose the following question:
Question 1 Hadwiger-Nelson problem代写
(The p–adic Hadwiger-Nelson problem). Is it true that there exists a universal constantB (independent of p) such that
χBor (QGQp ) ≤ B,
holds as p ranges over all primes of the form 4k + 3?
Remark 1.3
(Some set theoretic considerations). Let S be the subset of R2 defined by
S = {(q1, q2) ± s : q1, q2 ∈ Q, s = (√2, 0), (0, √2), (√2, √2), (−√2, √2)}.
Soifer and Shelah [16, section 3] define the graph tt2 as the Cayley graph of R2 with respect to S, and prove the intriguing theorem that the value of the chromatic number of tt2 depends on the choice of axioms for set theory. More precisely, they showed that under ZFC, χ(tt2) = 4 holds, while if one opts for the axiomatic system (the consistency of this system is proved by Solovay [17]) ZF+ DC+ LM (that is, ZF combined with the axiom of dependent choice, and the axiom that every subset of R is Lebesgue measurable), then tt2 does not even admit a proper coloring with ℵ0 colors. Let Gn,rdenote the quadratic graph associated the canonical quadratic form of signature (r, n − r) over Rn.Theorem 1.1 shows that if 1 ≤ r ≤ n − 1, then
(2) χ(Gn,r) ≤ χBor (Gn,r) = ℵ0. Hadwiger-Nelson problem代写
If the value of χ(Gn,r) turns out to be finite, then one obtains another (in our opinion more straight-forward, though less dramatic) example of a topological graph with the type of behavior `a la Soifer-Shelah.
For a field F and an integer n ≥ 2, the regular graph associated to the ring of n × n matrices over F , denoted by Γn(F ), has the vertex set GLn(F ) (general linear group over F ), where two vertices x, y ∈ GLn(F ) are adjacent if det(x + y) = 0. Regular graphs (for arbitrary rings) were introduced in [2] and the study of their chromatic number was initiated in [1]. For motivations and more details,we refer the reader to Section 4. As a corollary of Theorem 1.1, we answer question 525 from [6] by proving the following theorem:
Theorem 1.4.
Let F be a local field of characteristic zero and n ≥ 2. Then the Borel chromatic number of the regular graph Γn(F ) is infinite.
Remark 1.5. It is very likely that Theorems 1.1 and 1.4 equally hold over local fields of positive characteristic. The details need to be worked out.
This article is organized as follows. In section 2 we will set some notation and briefly explain the ideas behind the spectral bound used later. Sections 3 and 4 are devoted to the proofs of Theorem1.1 and Theorem 1.4.
2 Preliminaries Hadwiger-Nelson problem代写
In this section, we will review some of the ideas in the beautiful recent work [3] to prove an analog of the Hoffman bound for certain Cayley graphs of the additive group of the Euclidean space Rn.
2.1 The chromatic number of self-adjoint operators
Let G = (V, E) be a finite graph and consider the Hilbert space L2(V ) of all complex-valued functionsL2(V ) defined by Af (v) =vw∈E f (w) is self-adjoint. It is easy to see that the numerical range of A
W (A) := {(Af, f ) : “f “2 = 1},
is equal to [λn−1, λ0], where λ0 ≥ λ1 ≥ · · · ≥ λn−1 is the spectrum of A. It is also easy to verify that a subset I ⊆ V is independent if and only if for all f ∈ L2(V ) supported on I, one has (Af, f ) = 0. Hadwiger-Nelson problem代写This novel interpretation of independent sets is used in [3] to prove an analog of the Hoffman boundfor certain Cayley graphs of the additive group of the Euclidean space Rn. As we will need to work in a slightly more general framework, it will be useful to briefly go oversome of the key points of [3]; for details, we refer the reader to the original paper.
Let (V, Σ, µ) be a finite measure space, consisting of a set V , a σ-algebra Σ on V , and a measureµ.
Consider the Hilbert space L2(V ) with the inner product:
L2(V ) = {f : V → C measurable : ∫V |f |2 dµ < ∞}, (f, g) = ∫V f (x)g(x) dµ(x).
For a bounded and self-adjoint operator A : L2(V ) → L2(V ), one can show that the numerical range of A defined by
W (A) = {(Af, f ) : “f “2 = 1},
is an interval in R. We denote the endpoints of W (A) by
m(A) := inf{(Af, f ) : “f “2 = 1}, M (A) := sup{(Af, f ) : “f “2 = 1}.Hadwiger-Nelson problem代写
Deftnition 2.1. Let A : L2(V ) → L2(V ) be a bounded, self-adjoint operator. A measurable set I ⊆ V is called an independent set for A if (Af, f ) = 0 for each f ∈ L2(V ) which vanishes almost everywhere outside of I. Moreover the chromatic number of A, denoted by χ(A), equals the least number k such that one can partition V into k independent sets of A.
The following result [3, Theorem 2.3] is analogous to the well-known Hoffman bound for finite graphs:
Theorem 2.2. Let A : L2(V ) → L2(V ) be a nonzero, bounded and self-adjoint operator. Moreover assume that χ(A) < ∞. ThenM (A)
(3) 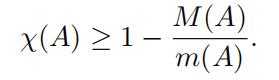
Remark 2.3. Hadwiger-Nelson problem代写
Similar to Hoffman bound, when A ƒ= 0 and χ(A) < ∞ the proof of the above theorem shows that m(A) < 0 and M (A) > 0.
We now relate this theorem to the Borel chromatic number of Cayley graphs with the vertex set F n, where F is R or a p-adic field Qp. All that follows is parallel to [3], where the case F = R is dealt with; in fact the arguments in [3] carry over to the p-adic case without any effort. For the convenience of the reader we will briefly discuss the key points.Hadwiger-Nelson problem代写
For the rest of this subsection, let F be either R or a p-adic field Qp with the ring of integers Zp. We will also assume that S ⊆ F n is a symmetric (i.e.,−S = S), Borel measurable set (with respect to the σ-algebra generated by the open sets), which doesnot contain the origin in its closure. The Cayley graph Cay(F n, S) has the vertex set F n, where twovertices x, y ∈ F n are adjacent if and only if x − y ∈ S. The goal is to find a spectral bound for the Borel chromatic number of this graph.
Let µ be a finite Borel measure on F n with support contained in S.
Therefore µ is a Radon measure [9, Theorem 7.8]. We will also assume that µ is symmetric, i.e., µ(−A ) = µ(A ) holds for all Borel measurable sets A . This measure produces a bounded, self-adjoint operator
Aµ : L2(F n) → L2(F n), f ›→ f ∗ µ,
where f ∗ µ(x) = F n f (x − y) dµ(y). One can easily see that since the support of µ is contained in S, any Borel measurable independent set I of Cay(F n, S) is also an independent set of Aµ (see [3, Section 3.1]). One can show that the Borel chromatic number of Cay(F n, S) is finite when S ⊆ F n is a bounded set with the above properties. This will be proved later (see Lemma 3.3). Therefore by
Theorem 2.2 we have Hadwiger-Nelson problem代写
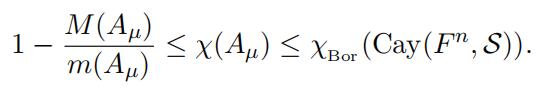
The numerical range of Aµ can now be determined using Fourier analysis. Below, we will review some of the basic properties of the Fourier transform over local fields. For more detail we refer the reader to [11, 20]. For F = R, we will use the character
ψ : R → C∗, ψ(x) = exp(2πix).
When F = Qp, for x ∈ Qp, we write nx for the smallest non-negative integer such that pnx x ∈ Zp. Let rx ∈ Z be such that rx ≡ pnx x (mod pnx ). It is well-known that the following map (called the Tate character)
(5) ψ : Qp→ C∗, ψ(x) = exp . 2πirx Σ ,
is a non-trivial character of (Qp, +) with the kernel Zp. We will denote by dx a Haar measure on F . When F = Q , we assume that it is normalized such that dx = 1. We will also use dx for theproduct (Haar) measure dx1 · · · dxn on F n. Moreover for a Borel set E ⊆ F n we use |E| = E dx to denote the measure of E.
The Fourier transforms of f ∈ L1(F n) and µ are respectively defined by the integrals
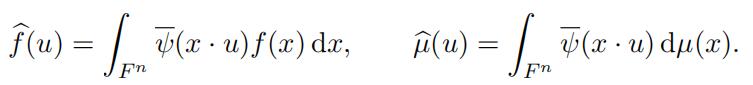
Here x · u is the standard bilinear form on F n, and ψ is the complex conjugate of ψ. By Plancherel’s theorem the Fourier transform extends to an isometry on L2(F n) and so for any f ∈ L2(F n) we have
(6) (Aµf, f ) = (Aµf , f ) = (f ∗ µ, f ) = (µf , f ).
Lemma 2.4.
Let µ be a symmetric finite Borel measure on F n with support contained in S. Then the numerical range of Aµ is given by
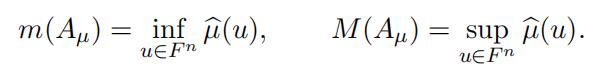
Proof. From (6) combined with the fact that the Fourier transform on L2(F n) is an isometry, we deduce that the numerical range of the operator Aµ is the same as the numerical range of the multiplicative operator g ›→ µg. Since µ is a symmetric finite Borel measure, then µ is a continuous, real-valued and bounded function. Now let g ∈ L2(F n) with “g“2 = 1. Evidently
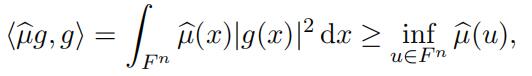
and so m(Aµ) ≥ infu∈F n µ(u). Now let ε > 0 and pick x0 ∈ F n with µ(x0) ≤ infu∈F n µ(u) + ε. Let Bδlim ∫21 (x)µ(x). B | .dx = lim 1 ∫µ^(x) dx = µ^(x0),where 1Bδ is the characteristic function of Bδ. Hence
m(Aµ) µ(x0) inf µ(u) + ε,u∈F
and therefore we have m(Aµ) = infu∈F n µ(u). Similarly we have M (Aµ) = supu∈F n µ(u).
We can now summarize these in the following theorem.
Theorem 2.5 (Bachoc-DeCortede-Oliveira-Vallentin [3]). Let F be either R or a p-adic field Qp and let S be a bounded, symmetric (i.e., −S = S) Borel measurable subset of F n which does not contain the origin in its closure. Then for any symmetric, finite Borel measure µ on F with support contained in S we have
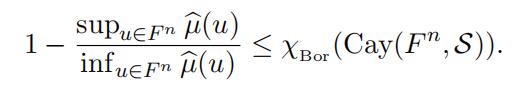
(7)
2.2 Quadratic and hyperbolic graphs
We first recall the general notion of a quadratic space. For more details we refer the reader to [14, Chapter IV]. Let F be an arbitrary field of characteristic different from 2 and let V be a finite dimensional vector space over F . A function Q : V → F is called a quadratic form on V if
(a)Q(ax) = a2Q(x) for a ∈ F and x ∈ V.
(b)The map (x, y) ›→ Q(x + y) − Q(x) − Q(y) is a bilinear
Such a pair Q = (V, Q) is called a quadratic space. For each quadratic space Q = (V, Q) we then obtain a symmetric bilinear form on V defined by
(8) (x, y) := 2 (Q(x + y) − Q(x) − Q(y)) = 2 (Q(x) + Q(y) − Q(x − y)).Hadwiger-Nelson problem代写
We say Q = (V, Q) is non-degenerate when the bilinear form (8) is non-degenerate. In this paper, we will only consider non-degenerate quadratic spaces. If Q = (V, Q) and Qj = (V j, Qj) are two quadratic spaces, a linear map f : V → V j such that Qj ◦ f = Q is called a morphism (or metric morphism) of Q into Qj; we say Q is isomorphic to Qj when f is a vector space isomorphism.
Deftnition 2.6.
For a given a quadratic space Q = (V, Q), the quadratic graph, denoted by QGQ, is defined as follows. The vertex set of QGQ coincides with the vector space V . Vectors v, w ∈ V form an edge in QGQ if and only if Q(v − w) = 1.
Let Q = (V, Q) be a non-degenerate quadratic space over F . It is well known that Q is isotropic if and only if it can be expressed in an appropriate basis (ei)1≤i≤n for V as
(9) Q(x1e1 + · · · + xnen) = x1x2 + a3x2 + · · · + anx2 .
In particular, the restriction of Q to the 2-dimensional subspace H spanned by e1 and e2 takes the form
(10) Q(x1e1 + x2e2) = x1x2.
The (unique up to isomorphism) quadratic space H = (H, Q|H ) (or, H(F ) if the underlying field F is to be emphasized) is often referred to as the hyperbolic plane (over F ). The associated quadratic
graph to the hyperbolic plane (over the field F ) will be called the hyperbola graph over F , and denoted by HG(F ). In other words,
HG(F ) = Cay(F 2, S), S = {(x, y) ∈ F 2 : xy = 1}.
Note that the map F 2 → V defined by (x1, x2) ›→ x1e1 + x2e2 embeds HG(F ) as an induced subgraph of QGQ when Q is an isotropic quadratic written in the form (10). If F is moreover a topological field, the image of this map is a closed subset of V . Therefore we have the following simple fact.
Lemma 2.7. Let F be an arbitrary field of characteristic different from 2 and let Q = (V, Q) be an isotropic quadratic space over F . Then χ(QGQ) ≥ χ(HG(F )). Moreover, if F is a topological field, then
χBor (QGQ) ≥ χBor (HG(F )).
3 Proof of the main theorem
In this section we will prove Theorem 1.1. In the first two subsections, we will give the proof for the real and p-adic isotropic forms. In the last subsection, we will deal with the (easier) case of anisotropic forms. Before embarking on the proof in the isotropic case, we would like to show that Theorem 1.1 cannot be proven by simply pointing to an infinite clique. Recall that the clique number of a graphG, denoted by ω(G) is the largest cardinal c such that G contains a complete subgraph on c vertices. We now have
Proposition 3.1.
Let Q = (V, Q) be a quadratic space over an arbitrary field F of characteristic different from 2. Then the clique number of QGQ is bounded above independently of the ground field. More precisely,
ω(QGQ) ≤ dim V + 1.
Proof. Suppose v0j , v1j , . . . , vnj ∈ V form a clique in QGQ. For 1 ≤ i ≤ n, set vi = vij − v0j . HenceQ(vi) = 1, 1 ≤ i ≤ n and Q(vi − vj) = 1 for 1 ≤ i ƒ= j ≤ n. From (8) we deduce that (vi, vj) = 1 fori ƒ= j. For 1 ≤ i ≤ n, consider the following functionals
αi : V → F, w ›→ (w, vi).
We claim that α1, . . . , αn are linearly independent. In fact, evaluating Σn
ckαk = 0 at w = vi yields
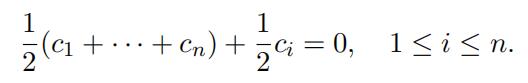
This system of linear equations has the unique solution c1 = · · · = cn = 0. From here, we conclude that n ≤ dim V ∗ = dim V , whence ω(QGQ) ≤ dim V + 1.
Remark 3.2.
The n + 1 vertices of a regular simplex of side 1 in Rn form a clique in the quadratic graph of the form x2 + · · · + x2 ; this shows that the above bound is indeed sharp.
Let us recall a number of basic facts about local fields. A local field is, by definition, a non-discrete locally compact topological field. It is a well-known fact that an archimedean local field is isomorphic to the field of real or complex numbers.
A non-archimedean local field is a complete field with respect to a discrete valuation that has a finite residue field,
and is isomorphic either to a finite extension of Qp (p is a prime number) or to the field of formal Laurent series Fq((t)) over a finite field with q = pfelements. A non-archimedean local field F comes with its ring of integers O, which is a local ring whose unique prime ideal p is principal. Let α be a generator for p, often referred to as a uniformizer. For m ∈ Z, we write pm for the ideal generated by αm. We have thus the following filtration of F :
F ⊇ · · · ⊇ p−2 ⊇ p−1 ⊇ p0 = O ⊇ p ⊇ p2 ⊇ · · · ⊇ {0}.
Let ” · ” denote the standard norm on F . When F is the field of real or complex numbers, this denotes the standard Euclidean norm. In the non-archimedean case, this norm is defined as follows: Every element of x ∈ F has a unique representation as x = uαm, where u is a unit of O and m ∈ Z.Let q denote the cardinality of the residue field O/p. The norm function ” · ” is defined by “x” = q−m.
Lemma 3.3.
Let F be a local field and let S ⊆ F n be a bounded, symmetric and Borel measurable set which does not contain the origin in its closure. Then χ Bor(Cay(F n, S)) < ∞.
Proof. First, we equip F n with the maximum norm define by
“x“ := max(“x1“, . . . , “xn“), x = (x1, . . . , xn).Hadwiger-Nelson problem代写
For 0 < c1 < c2, define the annulus with radii r1 and r2 by Sc1,c2 = {x ∈ F : c1 < “x” < c2}. SincenS is bounded and 0 ∈/ S, it follows that S ⊆ Sc1,c2 for some values of c1, c2 > 0. As Cay(F , S) is isomorphic to Cay(F n, (1/c1)S), up to passing to a dilation of S, we may assume that c1 = 1. Let us first consider the case F = R. Fix an integer m > c2 + 2. We claim that the map
c(x) = (|x1∫ mod m, . . . , |xn∫ mod m), x = (x1, . . . , xn).
provides a proper coloring. Assume c(x) = c(y); there are two possibilities: either |xi∫ = |yi∫ for all 1 ≤ i ≤ n, which implies “x − y” < 1, showing that x and y are not adjacent. Or, for some 1 ≤ i ≤ n, we have | |xi∫ − |yi∫ | ≥ m, which, in turn, implies that “x − y“ ≥ |xi − yi| > m − 2 > c2, proving that x and y are not adjacent. This gives the upper bound χBor(Cay(Rn, S)) ≤ mn.
Now let F be a non-archimedean local field with the residue field O/p of size q. Let α be a uniformizer, so “α“ = 1/q. Set A = O × · · · × O ⊆ F n. Since c1 = 1, we have S ∩ A = ∅. Choose an integer m such that qm ≥ c2. Each x ∈ F has a unique α-adic representation [10, 4.4 Proposition] of the form∞x = bjα , r ∈ Z, bj ∈ Fq.j=r
Define
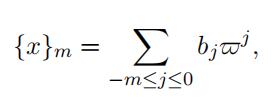
and consider the map
c(x) = ({x1}m, . . . , {xn}m), x = (x1, . . . , xn).
Suppose c(x) = c(y). This implies that in the expansion of each entry of x − y there are no terms αj with −m ≤ j ≤ 0. If for some 1 ≤ i ≤ n, xi −yi contains αr for some r < −m, then “x−y“ ≥ qm > c2. Otherwise, xi − yi, for all 1 ≤ i ≤ n, only contain αj for j > 0, hence “x − y“ < 1. In either case, we have x − y ƒ∈ S. Therefore χBor(Cay(F n, S)) ≤ q(m+1)n.
3.1 The case of isotropic real quadratic forms
The aim of this subsection is to show that if Q = (V, Q) is an isotropic quadratic space over R, then the Borel chromatic number of QGQ is infinite. From Lemma 2.7, it suffices to show that the Borel chromatic number of HG(R) is infinite. Fix a parameter T > 0 and consider the measurable set
(11) ST = .(x, y) ∈ R2 : xy = 1, e−T ≤ |x| ≤ eT Σ .
We will refer to the Cayley graph Cay(R2, ST ) as the T-chopped hyperbola graph.
Theorem 3.4. Hadwiger-Nelson problem代写
For T > 0, let Cay(R2, ST ) be the T-chopped hyperbola graph. Then
(12) 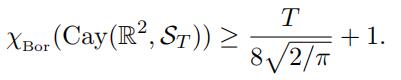
Notice that ST is a bounded symmetric set, i.e., ST = −ST which does not contain the origin in its topological closure. Hence the Borel chromatic number of Cay(R2, ST ) is finite by Lemma 3.3. For a measurable set E ⊆ R2, we define the following measure
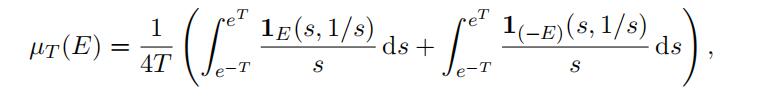
where 1E is the characteristic function of E. It is easy to verify that µT is a symmetric probability measure supported on ST .
Lemma 3.5. For T > 0 and arbitrary (x, y) ∈ R2 we have
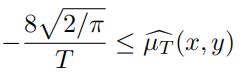
For the proof we will need the van der Corput’s lemma [18, Chapter VIII, Proposition 2].
Lemma 3.6.
Let φ : [a, b] → R be a function satisfying |φjj(t)| ≥ λ > 0 for all t ∈ [a, b]. Then
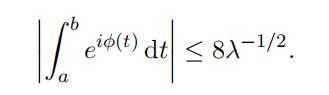
Proof of Lemma 3.5. A simple calculation shows that
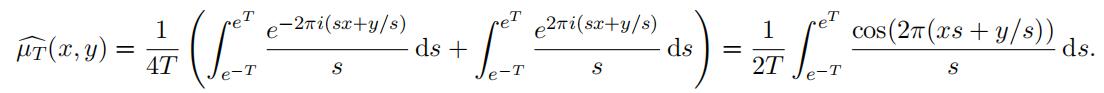
Using the substitution s = et, we have
1 ∫ Tt −tµ^T (x, y) = 2Tcos(2π(xe + ye−T)) dt.
Given x, y ∈ R, define
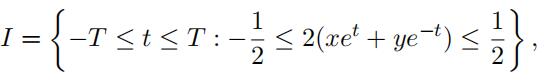
Σand Ij = [−T, T ] \ I. Clealy I is a closed interval and Ij is the union of at most two intervals I1j andpossibly I2j . Let φ(t) = 2π(xet + ye−t). By definition, for t ∈ Ij, we have |φjj(t)| = |φ(t)| ≥ π/2. Now
by applying Lemma 3.6 to the intervals I1j and I2j we have
.∫Ijjeiφ(t) dt. ≤ 8√2/π, j = 1, 2.
Extracting the real part, we obtain
(13) Ijcos(2π(xet + ye−t)) dt. ≤ 16√2/π.
On the other hand, for t ∈ I, we have cos(2π(xet + ye−t)) ≥ 0 and so
(14)Combining (13) and (14) we obtain
cos(2π(xet + ye−t)) dt ≥ 0.Hadwiger-Nelson problem代写
which implies that
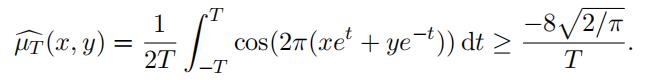
Proof of Theorem 3.4. Notice that µT is a symmetric measure with Supp(µT ) ⊆ ST . Since µT is a probability measure then obviously we have
(15) sup(x,y)∈R2µ^T (x, y) = 1.
From Lemma 2.4 we have m(AµT ) = inf(x,y)∈R2 µT (x, y), and so by Remark 2.3 and Lemma 3.5 we have
(16)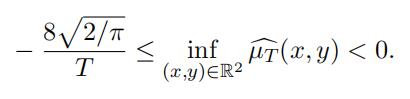
Hence by Theorem 2.5, (15) and (16) we obtain
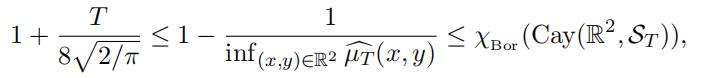
establishing our theorem.
For any T > 0, obviously χBor(x,y)∈R2(R2, ST ) ≤ χT(HG(R)), and so χBor
(HG(R)) = ∞ which implies that χBor (QGQ) = ∞ by Lemma 2.7, if Q = (V, Q) is an isotropic quadratic space over R.Hadwiger-Nelson problem代写
3.2 The case of isotropic padic quadratic forms
The proof in the p-adic case is similar to the one in the real case. We first remark that for a p-adic field F we have χBor (HG(F )) ≥ χBor (HG(Qp)). Hence in order to prove Theorem 1.1, analogous to thereal case, it suffices to show that the Borel chromatic number of hyperbola graphs HG(Qp) is infinite.
We also recall that the ring of integers of Qp is denoted by Zp and the maximal ideal of Zp by p. We will fix the uniformizer α = p which satisfies “α“p = 1/p. Hence
pk = {x ∈ Qp : “x“p ≤ p−k},
and we have the the filtration
Qp ⊇ · · · ⊇ p−2 ⊇ p−1 ⊇ p0 = Zp ⊇ p1 ⊇ p2 ⊇ · · · .
For k ∈ Z, define
Ck := {s ∈ Qp : “s“p = pk}.
Notice that Ck = p−k \ p−(k−1), and so |Ck| = pk − pk−1 where |Ck| denotes the Haar measure of Ck.Hadwiger-Nelson problem代写
For an integer T ≥ 1 consider the measurable set
(17) 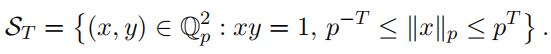
Note that ST is a bounded symmetric set which does not contain the origin in its closure. Similar to the real case, the Borel chromatic number of T-chopped hyperbola graph Cay(Q2, ST ) is finite by
Lemma 3.3.
Theorem 3.7. Let Cay(Q2, ST ) be the T-chopped hyperbola graph. Then
(18) χBor (Cay(Qp, ST )) ≥ 1 + (2T + 1)/4.
Let T ≥ 1 be an integer. For a measurable set E ⊆ Q2 we define the following measure
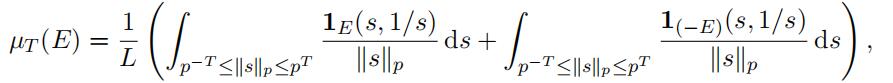
where L = (4T + 2)(1 − 1/p). It is easy to verify that the probability measure µT is a symmetric measure with Supp(µT ) ⊆ ST . By a straightforward calculation we obtain
(19)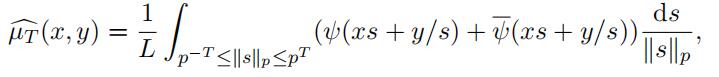
where ψ is an additive character of Qp with the kernel Zp, defined in (5). Hence our aim is to estimate µcT (x, y).
Following [12], for a positive integerr, we defifineincomplete Bessel function as follows
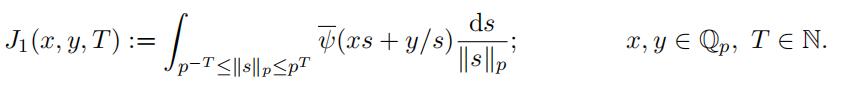
Hence
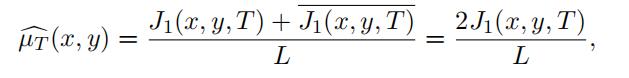
since J1(x, y, T ) is a real number.
Lemma 3.8. For an integer T ≥ 1 and arbitrary (x, y) ∈ Q2 we have
(20)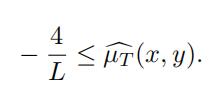
To prove this theorem we first need a few facts involving p-adic integrals:
Lemma 3.9. For k ∈ Z we have
(21)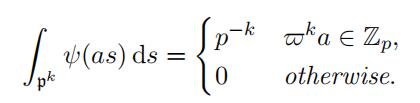
Proof. Let αka ∈ Zp. Then as ∈ Zp for all s ∈ pk and so ψ(as) = 1 which implies the first case. Suppose αka ƒ∈ Zp. Then ψa(s) := ψ(as) is a non-trivial character on pk and so its integral over pk is zero.
A direct consequence of this lemma is the following identity.Hadwiger-Nelson problem代写
Lemma 3.10. For a ∈ Qp with “a“p = pn and k ∈ Z we have
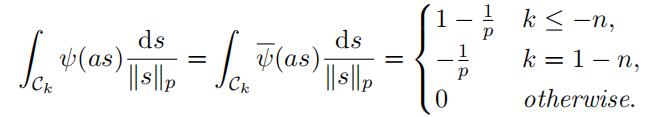
(22)
Proof. Since Ck = p−k \ p−(k−1) then
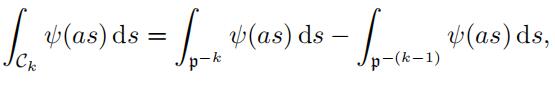
and so by (21) we obtain the equalities.
For a positive integer r and 0 ƒ= w ∈ Qp, define
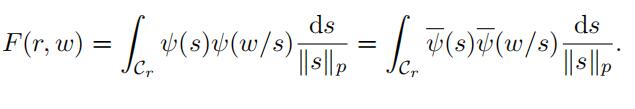
Evidently we have
(23) 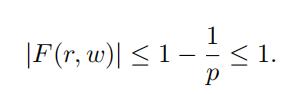
Lemma 3.11. Suppose that “w“p = pm and 1 ≤ r < m. Then F (r, w) ƒ≡ 0 as a function of w if and only if m is even and r = m/2.
Proof. See [12, Lemma 8(i)] also see [13, Lemma 10.10].Hadwiger-Nelson problem代写
Proof of Lemma 3.8. Throughout this proof we will let T ≥ 1 to be an integer. We show that for any (x, y) ∈ Q2:
(24) J1(x, y, T ) ≥ −2,
which from it we immediately deduce (20). Let x ƒ= 0, then from Lemma 3.10 we have
(25)Now let y = 0. Since ds“s“pis a Haar measure on the multiplicative group Q×p then we have
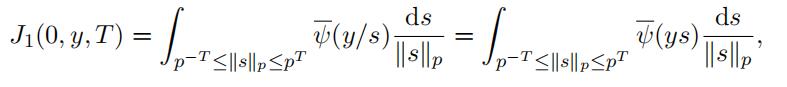
and so again by Lemma 3.10 we obtain
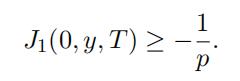
Therefore when xy = 0 we obtain (24). In the rest of the proof, we can thus assume that xy ƒ= 0. Let“y“p = pn2 . Using a change of variables we obtain
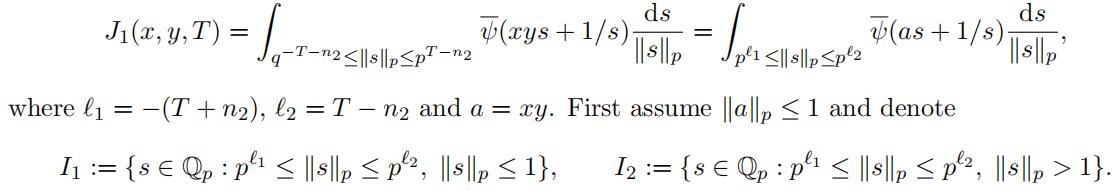
Hence from Lemma 3.10 we deduce that
(26)
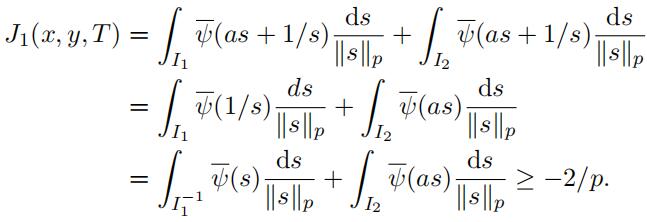
Therefore when “xy“p ≤ 1 we obtain (24). Next assume that “xy“p = “a“p > 1 and define
(27)
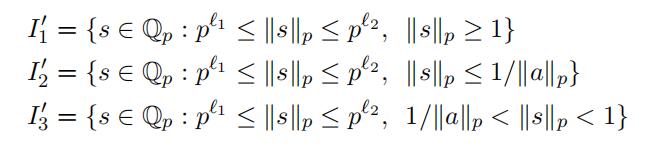
Hence again form Lemma 3.10 we have
(28)
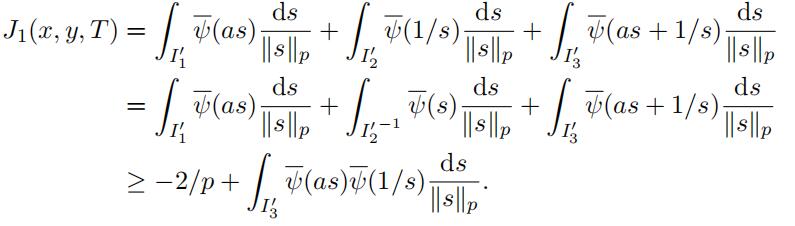
To complete the proof of Lemma 3.8 it remains to evaluate the last integral. We remark that
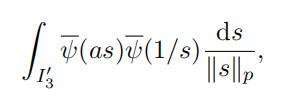
is a real number. Let “a“p = pm for some m ≥ 1. Hence we obtain the following finite sum
(29)
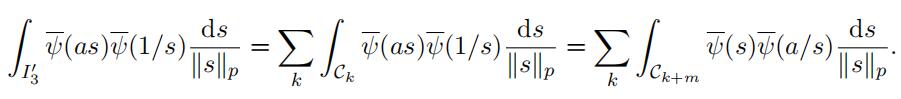
notice that 1 ≤ m + k < m since s ∈ I3j . Therefore by Lemma 3.11 and (23) we have
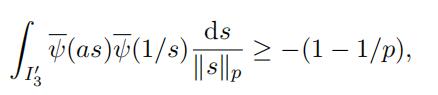
which by combining with (28) proves (24) when “xy“p > 1.
Since µT is a probability measure then sup(x,y)∈Q2 µ^T (x, y) = 1. Moreover, similar to the real case
and Lemma 3.8 we also have
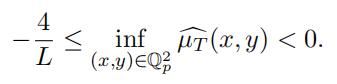
Therefore from Theorem 2.5 we have
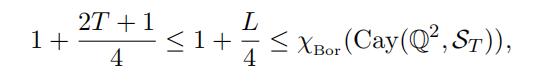
which proves Theorem 3.7. Now evidently we have
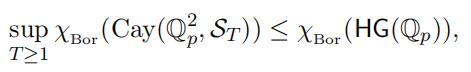
and so χBor (HG(Qp)) = ∞.
3.3The case of anisotropic quadratic forms Hadwiger-Nelson problem代写
Let F be a local field and let Q = (V, Q) be an anisotropic quadratic space with dim V ≥ 2. In this subsection we will show that χBor (QGQ) < ∞.Hadwiger-Nelson problem代写
Proof of Theorem 1.1 for anisotropic forms. Fix a norm on F and denote this norm as well as the associated supremum norm on V by ” · “. Set S = {v ∈ V : Q(v) = 1}, hence QGQ = Cay(V, S). We first show that S is a bounded set by proving that there exists a constant A > 0 such that for every v ∈ V , if “v“ ≥ A, then “Q(v)“ > 1.
By way of contradiction,
assume that there exists a sequence{vm}m≥1 in V such that “vm” → ∞ as m → ∞, while “Q(vm)” ≤ 1 for all m ≥ 1. For m ≥ 1,choose λm ∈ F such that “λm“”vm” = “λmvm” = 1. Hence λm → 0, from which it follows that Q(λmvm) → 0. Let wm = λmvm.
Since the unit sphere {v ∈ V : “v” = 1} is compact, after passing to a subsequence, we may assume that wm → w, where “w” = 1. The limit point w satisfies Q(w) = 0, which contradicts the assumption that Q is anisotropic. Therefore S is a bounded and measurable and so by Lemma 3.3, χBor (QGQ) is finite.
4Application to the chromatic number of regular graphs Hadwiger-Nelson problem代写
Let R be a ring (always assumed to contain the unity) and Z (R) denote the set of zero-divisors in R; set also R(R) = R \ Z (R). The regular graph of R, first introduced in [2], is the graph with the vertex set R(R), in which distinct vertices x, y ∈ R(R) are declared to be adjacent when x + y ∈ Z (R).The special case R = Mn(F ), where F is a field and Mn(F ) is the ring of n × n matrices over F .
Here, the vertex set coincides with the general linear group GLn(F ), with two vertices x, y ∈ GLn(F ) forming an edge if det(x + y) = 0. We will denote this graph by Γn(F ). The study of these regular graphs was initiated in [1], where the authors proved that the clique number of Γn(F ) is bounded by a function of n, independent of the underlying field F , assuming that the characteristic of F is not 2.More precisely, it is shown in [1] that for a field F of characteristic different from 2, we have
(30) ω(Γn(F )) ≤Cn,
where Cn = Σnk!.nΣ2 and ω(G) denotes the clique number of the graph G. Note that Cn does notdepend on F . Since ω(G) ≤ χ(G) for every graph G, it would be interesting to know whether or notan inequality of the form (30) can be established that is also independent of F . We can now prove Theorem 1.4:
Proof of Theorem 1.4. Without loss of generality we can assume that n = 2. For x, y ∈ F define
(31) ax,y := .1 −2xΣ . 1 0Σ = .1 − 4xy −2xΣ ∈ GL2(F ).
A simple computation shows that Hadwiger-Nelson problem代写
det(ax1,y1 + ax2,y2 ) = 4 − 4(x2 − x1)(y2 − y1).
Hence, vertices ax1,y1 and ax2,y2 of Γ2(F ) are adjacent if and only if (x2 − x1)(y2 − y1) = 1. Note also that since F has characteristic zero, the map (x, y) ›→ ax,y is a injective and continuous. This implies
that the induced subgraph on the set A = {ax,y : x, y ∈ F }, is isomorphic to HG(F ). Note that the alternative description of A as
A = ..x yΣ : x, y, z ∈ F, x − yz = 1Σ ,
makes it clear that A is closed, and hence Borel. This implies that the restriction of any finite Borel coloring of Γ2(F ) to A would yield in a Borel coloring of HG(F ) and so
χBor (Γ2(F )) ≥ χBor (HG(F )) = ∞,by Theorem 1.1.
Acknowledgement Hadwiger-Nelson problem代写
During the completion of this work, M.B. was supported by a postdoctoral fellowship from the Uni- versity of Ottawa. He wishes to thank his supervisor Vadim Kaimanovich. The authors are grateful to Saeed Akbari, Boris Bukh, Camelia Karimianpour and Hadi Salmasian with whom the authors discussed various parts of this paper.
References Hadwiger-Nelson problem代写
[1] Akbari, M. Jamaali, and S. A. Seyed Fakhari. The clique numbers of regular graphs of matrix algebras are finite. Linear Algebra Appl., 431(10):1715–1718,2009. [2]David F. Anderson and Ayman Badawi. The total graph of a commutative ring. Algebra, 320(7):2706– 2719,2008. [3]ChristineBachoc, Evan DeCorte, Fernando M´ario de Oliveira Filho, and Frank Vallen Spectral bounds for the independence ratio and the chromatic number of an operator. Israel J. Math., 202(1):227–254, 2014. [4]ChristineBachoc, Gabriele Nebe, Fernando M´ario de Oliveira Filho, and Frank Vallen Lower bounds for measurable chromatic numbers. Geom. Funct. Anal., 19(3):645–661, 2009. [5]Boris Bukh. Measurable sets with excluded distances. Funct. Anal., 18(3):668–697,2008. [6]Peter Cameron. Research problems from the BCC22. Discrete Math., 311(13):1074–1083, 2011.[7]FernandoM
´ario de Oliveira Filho and Frank Vallen Fourier analysis, linear programming, and densities of distance avoiding sets in Rn. J. Eur. Math. Soc. (JEMS), 12(6):1417–1428, 2010.
[8]J. Falconer. The realization of distances in measurable subsets covering Rn. J. Combin. Theory Ser. A, 31(2):184–189,1981. [9]Gerald Folland. Real analysis. Pure and Applied Mathematics (New York). John Wiley & Sons, Inc., New York, second edition, 1999. Modern techniques and their applications, A Wiley-Interscience Publication. [10]Ju¨rgenNeukirc Algebraic number theory, volume 322 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Springer-Verlag, Berlin, 1999. Translated from the 1992 German original and with a note by Norbert Schappacher, With a foreword by G. Harder.Hadwiger-Nelson problem代写 [11]Walter Fourier analysis on groups. Wiley Classics Library. John Wiley & Sons, Inc., New York,1990. Reprint of the 1962 original, A Wiley-Interscience Publication. [12]J. Sally, Jr. and M. H. Taibleson. Special functions on locally compact fields. Acta Math., 116:279–309, 1966. [13]Paul Sally, Jr. An introduction to p-adic fields, harmonic analysis and the representation theory of SL2.Lett. Math. Phys., 46(1):1–47, 1998.[14]-P. Serre.
A course in arithmetic. Springer-Verlag, New York-Heidelberg, 1973. Translated from the French, Graduate Texts in Mathematics, No.7.
[15]Alexander Soifer. The mathematical coloring book. Springer, New York, Mathematics of coloring andthe colorful life of its creators, With forewords by Branko Gru¨nbaum, Peter D. Johnson, Jr. and Cecil Rousseau. [16]Alexander Soifer and Saharon Shelah. Axiom of choice and chromatic number: examples on the plane. Combin. Theory Ser. A, 105(2):359–364,2004. [17]Robert M. A model of set-theory in which every set of reals is Lebesgue measurable. Ann. of Math. (2), 92:1–56,1970. [18]Elias M. Stein. Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals, volume 43 of Princeton Mathematical Series. Princeton University Press, Princeton, NJ, 1993. With the assistance ofTimothy Murphy, Monographs in Harmonic Analysis, III.Hadwiger-Nelson problem代写 [19] A. Sz´ekely. Erd˝os on unit distances and the Szemer´edi-Trotter theorems. In Paul Erd˝os and his mathematics, II (Budapest, 1999), volume 11 of Bolyai Soc. Math. Stud., pages 649–666. J´anos Bolyai Math. Soc., Budapest, 2002. [20]H. Taibleson. Fourier analysis on local fields. Princeton University Press, Princeton, N.J.; University of Tokyo Press, Tokyo,1975. [21]R. Woodall. Distances realized by sets covering the plane. J. Combinatorial Theory Ser. A, 14:187–200, 1973.Bardestani, Department of Mathematics and Statistics, University of Ottawa, 585 King Edward, Ottawa, ON K1N 6N5, Canada.
E-mail address: [email protected]
Mallahi-Karai, Jacobs University Bremen, Campus Ring I, 28759 Bremen, Germany.
E-mail address: [email protected]

更多其他:C++代写 java代写 r代写 代码代写 金融代写 python代写 web代写 物理代写 数学代写 考试助攻 C语言代写 finance代写 code代写 作业帮助 数据分析代写 analysis代写
