可集成系统代写 MA6522/MA7522代写

MA6522/MA7522 Integrable Systems Assessment 2

可集成系统代写 Suppose that u(x, t) is a solution of the Korteweg-de Vries equationut + 6uux + uxxx = 0,such that u, ux and uxx → 0 as |x| → ∞.

Assessment 1 consists of four written questions and has to be handed in by 4:00pm on Wednesday, March 27th, 2019.

1. Suppose that u(x, t) is a solution of the Korteweg-de Vriesequation  可集成系统代写

u_t + 6uu_x + u_xxx = 0,

such that u, u_x and u_xx → 0 as |x| → ∞. Show that

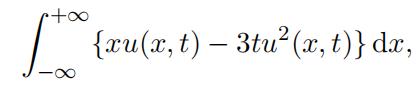
is a conserved quantity.   Determine the value of this conserved quantity for   the single-soliton solution  可集成系统代写

u(x, t) = 2κ²sech²[κ(x − 4κ²t)], κ > 0.

Hint: You may assume that

[10 marks]

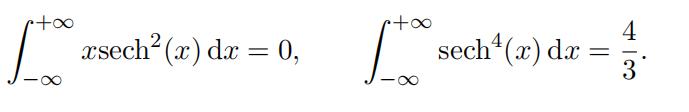
2. Consider the modified KdVequation

u_t = u_xxx − 6u²u_x.

(a)Presentit as a Hamiltonian equation (without proof). [4 marks]  可集成系统代写

(b)Define the linear operators L = D²− u² − u_x and

M = αD³ + aD_x + b,

where α is constant, a and b are dependent of x and t. Determine α, a and b such that L and M satisfy the Lax equation for the modified KdV equation. [14 marks]

3. Showthat the bilinear form of the KP equation (two-dimensional KdV) 可集成系统代写

D_x(u_t + 6uu_x + u_xxx) + 3u_yy = 0

is

(D_tD_x + D4 + 3D2)(f · f ) = 0,

where u(x, t) = 2 ^∂2

ln f (x, y, t). [12 marks]

4. Consider the map definedby 可集成系统代写

 

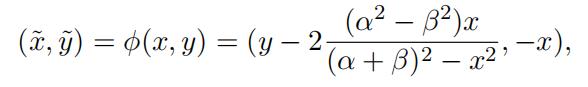
where α and β are constant.

(a)Showthat it is a symplectic  [4 marks]  可集成系统代写

(b)Show that the function definedby

I(x, y) = (x² − (α + β)²)(y² − (α + β)²) + 2(α² − β²)xy

is invariant under the map and thus it is a integrable map. [6 marks]

其他代写：代写CS C++代写 java代写 matlab代写 web代写 加拿大代写 app代写 作业代写 物理代写 数学代写 考试助攻 paper代写 r代写 金融经济统计代写 代写CS作业

合作平台：essay代写 论文代写 写手招聘 英国留学生代写