SUMMER TERM 2018
ECON3014: GAME THEORY
博弈论代考 Both agents value the object at v > 0. Agents submit their bids simultaneously and independently in the sealed envelopes.
Answer any THREE questions. All questions carry equal weight.
In cases where a student answers more questions than requested by the examination rubric, the policy of the Economics Department is that the student’s fifirst set of answers up to the required number will be the ones that count (not the best answers). All remaining answers will be ignored.
1.Two agents participate in a fifirst-price sealed-bid auction for an object.
Both agents value the object at v > 0. Agents submit their bids simultaneously and independently in the sealed envelopes. An agent who submitted the largest bid receives the object and payshis bid. If two agents submit the same bids, the winner is chosen randomly with equal probabilities. 博弈论代考
(a) Formalize this situation as a game and suggest the most appropriate equilibrium notion
(b) Find all equilibria in pure strategies.
(c) Are there any other symmetric equilibria? If there are, fifind at least one of them.

2. Consider a road network on the diagram below. There are 5000 drivers who wish to travel from point A to B. 博弈论代考
The travel time in minutes on the A → C road is tA→C = XA→C/100,where XA→C is the number of travelers taking that route. The travel time in minutes on the A → D road is a constant 45 minutes. The same travel times hold on the other two roads (see the diagram below). All drivers decide on the route they take simultaneously and independently of each other. Each driver tries to get from A to B as soon as possible.
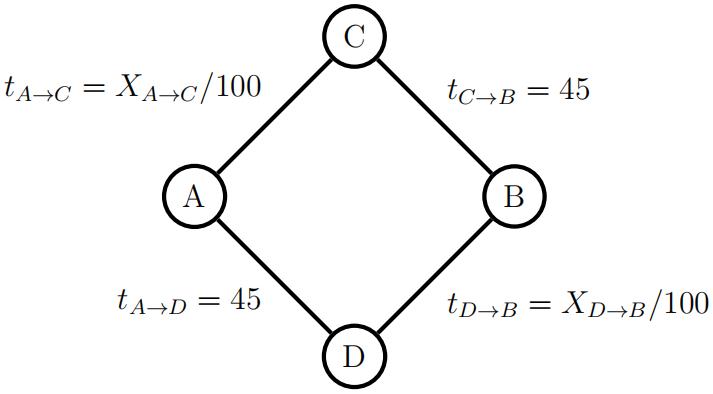
(a) Solve for an equilibrium in pure strategies.
(b) Suppose the additional one-way road from C to D is built and the travel time on this road is zero (see the diagram below). Solve for an equilibrium in pure strategies and compare your answer to the one you gave in 2a.
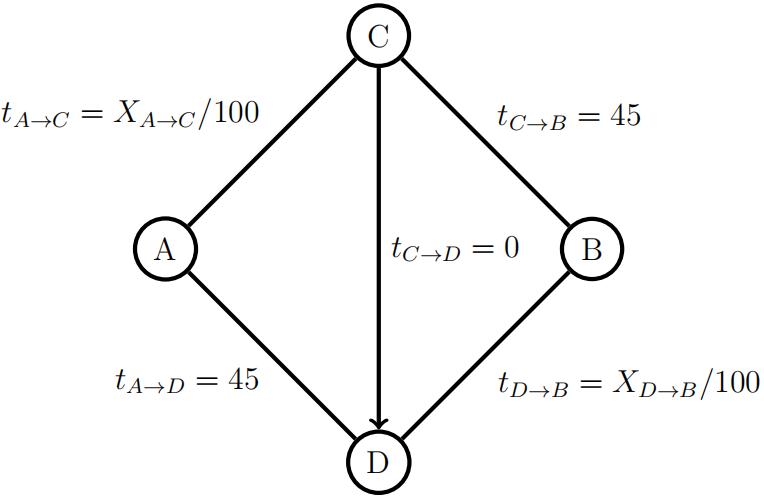
(c) Suppose the road between C and D is converted to a two-way road. The travel time on this road is still zero. Solve for an equilibrium in pure strategies and compare your answer to the ones you gave in 2a and 2b.
3.Two fifirms are competing with each other in the market for homogenous good.
Each fifirm can produce the good at zero marginal cost. There are two periods. In the fifirst period,fifirm 1 produces some amount of good q1. In the second period, fifirm 2 observes the choice of fifirm 1 and produces some amount of good q2. The output of both fifirms is sold in the second period in the market with a demand
Q = A − P.
Both fifirms maximize their profifits.
(a) Formalize this game and suggest the most appropriate notion of equilibrium. Solve the game. 博弈论代考
(b) Assume that in the second period fifirm 2 observes the choice of fifirm 1 with probability α and does not observe anything with the remaining probability (1 − α). Find an equilibrium in pure strategies.
(c) Assume that instead of observing the output of fifirm 1, fifirm 2 observes a signal y such that y = −1 if q1 ≥ kA and y = q1 otherwise. The parameter k ∈ (1/3, 1/2) is commonly known. Find an equilibrium in pure strategies. Provide intuition.
4. Consider a marriage market with n men and n women. Men are indexed by i ∈ {1, 2, .., n} and women are indexed by j ∈ {1, 2, .., n}. 博弈论代考
All women have the same preferences over men: if i > i0 any woman prefers mi 0 to mi . Each man i has the preferences described by the following utility function:
ui(wj ) = 2n − |i − j + 1/3|.
If a man does not marry, he gets a utility of zero.
(a) Suppose n = 3. Find a stable matching in this market.
(b) Find a stable matching for any n.
(c) Is there a unique stable matching in this market? Provide the proof for your answer.

