MT5863 Semigroups
半群代写 1. (a) Define a right zero element in a semigroup, and a right zero semigroup. [2](b) Denote by Tn the full transformation monoid on {1, . . . , n}.
EXAM DURATION: 2 hours
EXAM INSTRUCTIONS: Attempt ALL questions.
The number in square brackets shows the maximum marks obtainable for that question or part-question.
Your answers should contain the full working required to justify your solutions.
INSTRUCTIONS FOR ONLINE EXAMS:
Each page of your solution must have the page number, module code, and your student ID number at the top of the page. You must make sure all pages of your solutions are clearly legible.
1. 半群代写
(a) Define a right zero element in a semigroup, and a right zero semigroup. [2]
(b) Denote by Tn the full transformation monoid on {1, . . . , n}. A mapping α ∈ Tn is said to be constant if there exists y ∈ {1, . . . , n} such that xα = y for all x ∈ {1, . . . , n}. Prove that a mapping α is a right zero of Tn if and only if it is a constant mapping. [2]
(c) Does Tn (n > 1) have left zeros? Justify your answer. [2]
(d) Prove that the set C ⊆ Tn of all constant mappings is an ideal, and that this ideal is minimal with respect to inclusion. [2]
(e) Prove that if D ⊆ Tn is a subsemigroup isomorphic to a semigroup of left zeros, then all the elements of D have the same image. [2]
(f) Exhibit an example of a subsemigroup E of T4 isomorphic to the left zero semigroup of order 4. Justify your answer. [2]
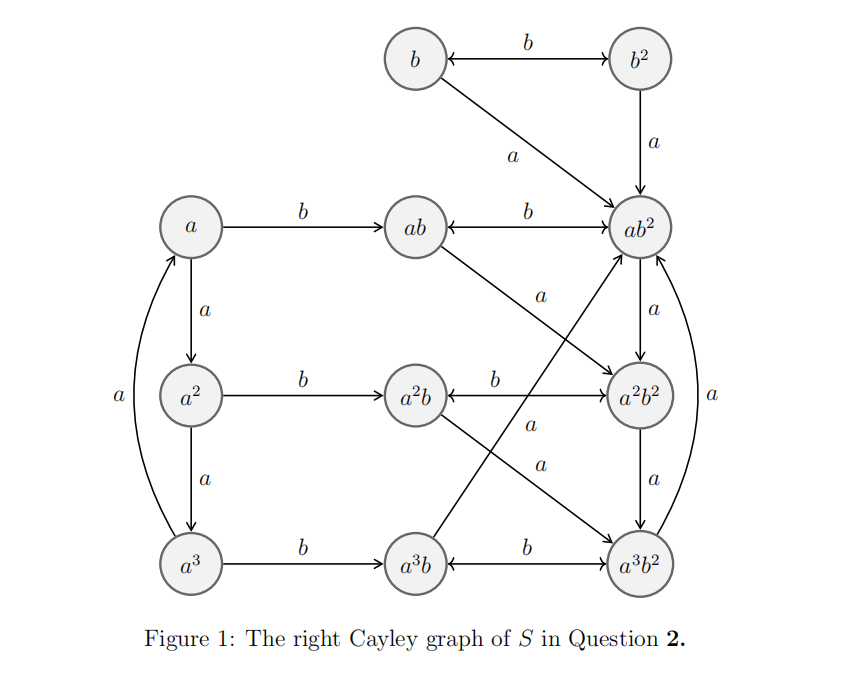
2.
Let S be the semigroup with 11 elements generated by two elements a, b whose right Cayley graph is shown in Figure 1.
(a) Compute the product a2b · ab2 in S. [1]
(b) List the R-classes of S. Justify your answer. [2]
(c) Is R a congruence relation on S? Justify your answer. [2]
(d) Compute and draw the left Cayley graph of S. Explain your method. [6]
(e) Which, if any, of the R-classes are ideals of S? Justify your answer. [2]
3. 半群代写
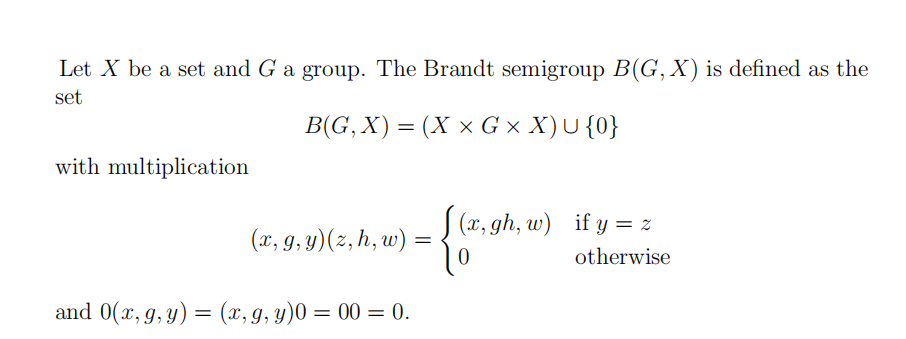
(a) Show that B(G, X) is a 0-simple semigroup. [2]
(b) Give the definition of an inverse semigroup and show that B(G, X) is an inverse semigroup. [2]
(c) Let H be a normal subgroup of G and let
ρH = {((x, g, y),(x, h, y)) | x, y ∈ X, gh−1 ∈ H},
which is an equivalence relation on B(G, X). Show that ρH is a congruence on B(G, X) and that
B(G, X)/ρH ≌ B(G/H, X). [4]
(d) Show that if σ is a congruence on B(G, X) and there are (x, g, y),(z, h, w) ∈ B(G, X) such that ((x, g, y),(z, h, w)) ∉σ then σ ⊆ ρG. [1]
(e) Show that if σ is a congruence on B(G, X) such that σ ⊆ ρG then there is a normal subgroup K ≤ G such that σ = ρK. [3]
(f) Show that if f : B(G, X) → T is a surjective homomorphism then T is either trivial or a Brandt semigroup. [2]
4. 半群代写
In this question let S be a regular semigroup.
(a) Show that each R-class R of S contains an idempotent e and that e is a left identity for R. [3]
(b) Let D be a D-class of S. For s ∈ D let Ls and Rs be the L– and R-classes of s, respectively. Prove that there is some d ∈ D such that LdRd = D. [3]
(c) Suppose S is such that aS = S for all a ∈ S. Show that for all x, s, t ∈ S, if xs = xt then s = t. [5]

