Dynamical systems
动力系统代写 d) Based on the fixed points in subtask b) and their indices in subtask c), address the following tasks without evaluating the stability exponents
1.
Bifurcation and indices Consider the dynamical system
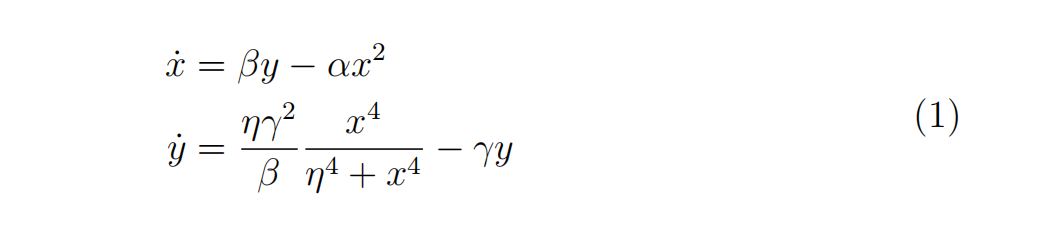
where α, β, γ and η are real parameters.

d) Based on the fixed points in subtask b) and their indices in subtask c), address the following tasks without evaluating the stability exponents
i. Find all bifurcations where fixed points are created or destroyed.
ii. Is the index conserved in the bifurcations?
iii. Discuss the possible types of fixed points that can be involved in the bifurcations.
2. 动力系统代写
Conservative systems Consider the dynamical system
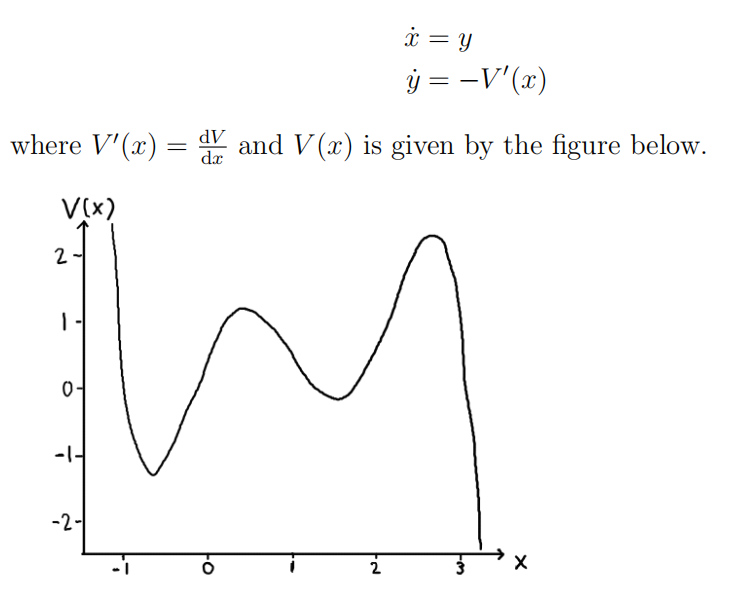
a) Sketch the phase portrait of this system and briefly explain how you obtain it. If you want to make the sketch by hand, you can either scan your solution, or take a photo of it.
b) For each fixed point you find in subtask a) do the following
i. highlight its stable and unstable manifolds in the phase portrait.
ii. indicate all regions in your sketch that contain closed orbits.
iii. verify that the indices of all closed orbits come out as expected.
The following subtasks are unrelated to subtasks a) and b)
c) Sketch the phase portrait of a dynamical system that has exactly one fixed point and two closed orbits.
d) Construct a dynamical system for the dynamical variables z and w that has an integral of motion E = wez+ z3we−w.
3. 动力系统代写
Lyapunov exponents of the damped driven pendulum Consider the damped driven pendulum
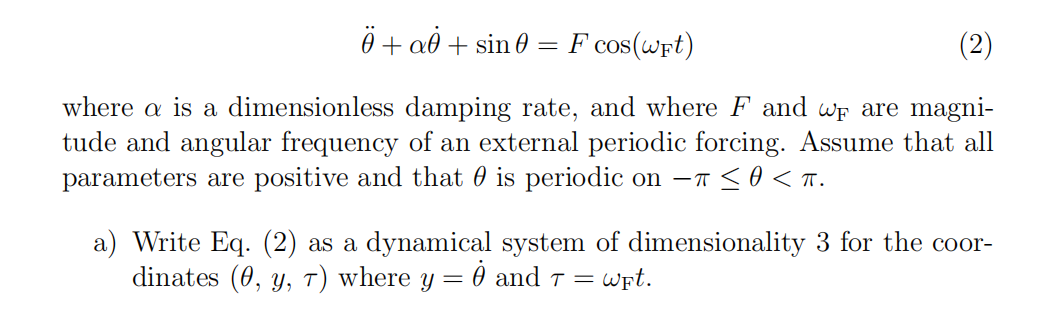
b) For the case F = 0, analytically determine the Lyapunov exponents of the system in subtask a) as functions of α. Explain the signs of the Lyapunov exponents.
c) Let F = 1 and ωF = 2/3 in what follows. For each of the values α = {0.1, 0.5, 2}, numerically integrate the system in subtask a) from an arbitrary initial condition. Make one plot showing the long-time asymptotes of the three resulting trajectories in the (θ, y) plane for a range of large τ .
d) Based on asymptotic trajectories similar to those in subtask c), use the method of successive QR-decompositions to numerically evaluate the Lyapunov exponents of the system in subtask a) as functions of α in the range 0 ≤ α ≤ 5 and address the following tasks
i. Make a plot containing your resulting Lyapunov exponents together with the analytical result (for F = 0) from subtask b).
ii. Do your results agree?
iii. If there are ranges where the results agree, explain why F does not matter much in these ranges.
iv. If there are ranges where the results do not agree, explain what happens in these ranges.

