Homework 1 Due 5-14 by 10:00 pm EST
加拿大统计代写价格 Then upload the PDF to Canvas Assignments by the due date. The recommended procedure is to download and print the homework (11 pages).
Instructions: Solve the problems in the spaces provided and save as a single PDF. Then upload the PDF to Canvas Assignments by the due date. The recommended procedure is to download and print the homework (11 pages). Fill in your solutions. Then scan the document and upload to Canvas Assignments. If this is not feasible for you, you may solve the problems on your paper, scan your solutions, then upload to Canvas. Neatness and presentation are important. Late homework not accepted. Show all work.
Total points: 30
1) Evaluate 加拿大统计代写价格
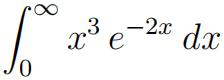
No need to show any work. Relate to the gamma distribution. (0.5 point)
2) Suppose the random variable X has the density given by
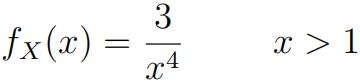
a) Find E[X]. (0.5 point)
b) Find V ar(X). (1 point)c) Find the cdf. Defifine for all real numbers. (1.5 points)
3) Suppose X ∼ U(−1, 1). Find
a) P(|X| > 4 1 ). (0.5 point)
b) the pdf of Y = X2 . Make sure to defifine the support of the density. (1.5 points)
4) Suppose that X ∼ Exp(1). For α > 0, β > 0, and −∞ < ν < ∞, find
a) the pdf of Y = αX β + ν. Make sure to defifine the support of the density function.(1.5 points)
b) E[Y ]. (1.5 points)
5) Let X be a random variable with density
![]() − ∞ < x < ∞
− ∞ < x < ∞
a) Find E[X]. (1 point)
b) Find V ar(X). (1 point)c) Find the cdf. Defifine for all real numbers. (1.5 points)
d) Find the moment generating function (mgf). Defifine the values t for which the mgfexists. (2 points)
6) Suppose that X and Y are jointly continuous random variables such that X ∼ U(0, 1) and
fY |X(y|x) = 1 x < y < x + 1.
Find P(X + Y < 1). (1.5 points)
7) Suppose X ∼ U(0, 1) and that conditional on X being observed, Y | x ∼ U(0, x). 加拿大统计代写价格
a) Find the joint density f(x, y). Defifine the support of the joint density function.(1 point)
b) Find the marginal density fY (y). Defifine the support of the density function.(1.5 points)
c) Calculate E[Y ] and V ar(Y ). (1.5 points)
(Hint: Try using Theorem A page 149 and Theorem B page 151 in text)d) Calculate Cov(X, Y ). (2 points)
8) The joint density function of X and Y is given by
![]() x > 0 y > 0
x > 0 y > 0
a) Find the conditional density f(x| y). Defifine the support with respect to x. (1 point)b) Find the conditional density f(y| x). Defifine the support with respect to y. (1 point)
c) Find the density function of Z = XY . Defifine the support of the density. (2 points)

9) Let X be a random variable having fifinite expectation µ and variance σ 2 . Let g be a twice difffferentiable function.
a) Show that
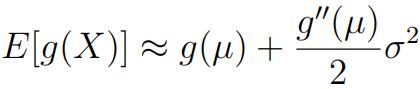
Hint: Expand g in a Taylor series about µ. Use the fifirst three terms and ignore the remainder. (1 point)
b) Let X be a Poisson random variable with mean λ. Show that if λ is not too small,then
V ar(![]() ) ≈ 0.25
) ≈ 0.25
Hint: Use the result from part a) to approximate E[ ![]() ]. (1.5 points)
]. (1.5 points)
10) In class we considered the distribution of the random variables X and Y
f(x, y) =![]() 0 ≤ y ≤ 1 − x 2 , −1 ≤ x ≤ 1
0 ≤ y ≤ 1 − x 2 , −1 ≤ x ≤ 1
a) Find the inverse cdf of Y . That is, fifind FY−1(y). (1.5 points)
We derived an algorithm for generating random variables from the joint distribution. The code to generate 1,000 observations in R is given below. Copy and paste the following code into R. Comments are preceded by the # sign.
u <- runif(1000) #generate 1,000 U(0,1) random variables
y <- 1-(1-u)^(2/3) #the inverse cdf method to generate y
x <- runif(1000,-sqrt(1-y),sqrt(1-y)) #x|y is U(-sqrt(1-y),sqrt(1-y))
plot(x,y) #scatterplot of x and y
b) Does it look like the points are uniformly distributed under the function y = 1−x2 for −1 ≤ x ≤ 1? (0.5 point) 加拿大统计代写价格
It is also true that x contains a sample of 1,000 random variables generated from the marginal fX(x) and y contains a sample of 1,000 random variables generated from the marginal fY (y). Just turn in the scatterplot of x and y. In a Windows environment you should be able to right click in the plot area to save it or print it.Optional problems to try for practice (taken from your text, do not turn in)
Page 67: 40ab
Page 69: 54, 55, 56, 58, 59, 61, 66, 67abc
Page 108: 14
Page 112: 43
Page 167: 13
Page 168: 14
Page 170: 44, 50
Page 171: 55, 56
More optional problems to try for practice (do not turn in)
1) Let X be a random variable with cumulative distribution function (cdf) 加拿大统计代写价格
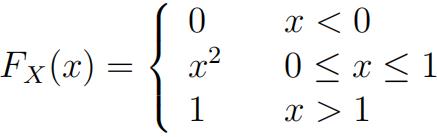
a) Find P(X > 0.5).
b) Find the median. This is the value m such that ![]() fX(x) dx = 0.5
fX(x) dx = 0.5
c) Find the standard deviation.
d) Let Y = ![]() . Find the pdf and the cdf of Y .
. Find the pdf and the cdf of Y .
2) Let X1, X2, . . . Xn be iid from Exponential(1/θ). That is
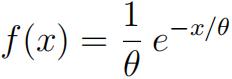 x > 0
x > 0
Calculate E[nX(1)] where X(1) is the smallest order statistic.
3) Let X1, . . . , Xn be independent and identically distributed (iid) random variables each with marginal density
f(x) = ![]() x > 0.
x > 0.
Find the pdf of the random variable
Y = 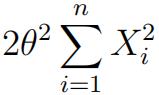
4) Let Z1 and Z2 be independent N(0, 1) random variables.
Calculate Cov(Z1 + Z2, Z1 − Z2).
5) If X ∼ N(0, σ2), fifind the pdf of Y = |X|. Make sure to defifine the support of the density function (the values of y where fY (y) > 0).
6) Suppose X ∼ N(µ, σ2 ). Find the pdf of Y = e X. This is known as the lognormal distribution. Make sure to defifine the support of the density.
7) Jill’s bowling scores are approximately normally distributed with mean 170 and stan-dard deviation 20, while Jack’s scores are approximately normally distributed with mean 160 and standard deviation 15. If Jack and Jill each bowl one game, then assuming that their scores are independent random variables, approximate the probability that
a) Jack’s score is higher.
b) the total of their scores is above 350.
8) The joint density of X and Y is given by 加拿大统计代写价格
f(x, y) = x e−(x+y) x > 0 y > 0
a) Determine if X and Y are independent.
If instead, f(x, y) were given by
f(x, y) = 2 0 < x < y 0 < y < 1
b) Determine if X and Y are independent.
c) Calculate Cov(X, Y ).
9) If X1 and X2 are independent U(0, 1) random variables, then the joint pdf of the order statistics (X(1), X(2)) is f(X(1), X(2))(x1, x2) = 2 0 < x1 < x2 < 1
For n ≥ 1 fifind P(nX(1) > X(2)). Calculate
![]() P(nX(1) > X(2))
P(nX(1) > X(2))
10) Let X1, X2 be iid N(0, 1). Let
Y1 = g1(X1, X2) = X1 + X2 Y2 = g2(X1, X2) = X1 − X2
a) Find the joint pdf f(y1, y2).
b) Are Y1 and Y2 independent?
c) What are the marginal distributions of Y1 and Y2?
11) Suppose that the conditional density of X given Y = y has an exponential distribution with parameter y. In addition, let Y ∼ Gamma(α, λ). Find the marginal density f(x)(this density will depend on parameters α and λ). 加拿大统计代写价格
12) Suppose X has the density given by
fX(x) = ex−ex− ∞ < x < ∞
a) Find the cdf FX(x).
The density of a distribution truncated on the left by a and the right by b is given by
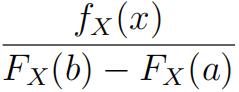 a < x < b
a < x < b
b) Find the truncated density when a = 0 and b = ∞.
13) Suppose the random variable X has the density given by
fX(x) = λ x−(λ+1) x > 1 , λ > 0
Find the density of Y = log X. Do you recognize this density?
14) The distribution given by
fX(x) =![]() x exp[−1/2(x/β) 2 ] x > 0, β > 0
x exp[−1/2(x/β) 2 ] x > 0, β > 0
is called the Rayleigh distribution.
a) Find E[X]. b) Find V ar(X).

