初等实分析作业代写 Elementary Real Analysis代写

Assignment 5- Elementary Real Analysis

初等实分析作业代写 Assume f ∈ C2(D). Show that f is convex in D if and only if the Hessian matrixD2f (x) is positive semi-definite for every x ∈ D.

1 . Suppose x, y, z, u satisfy the equation

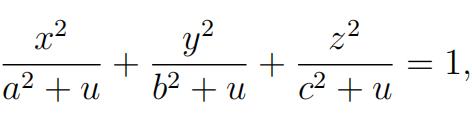
where a, b, c are constants. Prove that

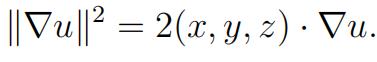
2 . (i) Assume f (x, y) is defined on a convex set E R2. Show that if f_x = 0 in E the  n f (x, y) only depends on y.  初等实分析作业代写

(ii) Show that the above convex condition can be replaced by a weaker condition, but some condition is required. For example when E is shaped like a horseshoe, the statement may be false.

3(Convex functions). Assume D Rⁿ  is a convex  domain and f : D →R is a function.

The function f is said to be convex if

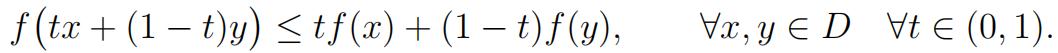
When the above ‘ ≤’ is replaced by ‘<’, we say f is strictly convex.

(i)Assume f ∈ C¹(D). Show that f is convex in D if and only if

f (y) ≤ f (x)+ ∇f (x) · (y — x), ∀x, y ∈ D.   初等实分析作业代写

(ii)Assume f ∈ C²(D). Show that f is convex in D if and only if the Hessian matrix

D²f (x) is positive semi-definite for every x ∈ D.

4(Continuity of the distance function). Assume x, y Rⁿ , E Rⁿ , and ρ is a distance function on Rⁿ .

(i)Fixedany y Rⁿ .  Show that ρ(x, y) is a uniform continuous function for x ∈Rⁿ .

(ii)Letρ(x, E) := inf ρ(x, y). Show that ρ(x, E) is a uniform continuous function for x ∈ Rⁿ .  初等实分析作业代写

(iii)Let a ∈ R. Show that the set G_a = {x ∈ Rⁿ : ρ(x, E) < a} is open and the set F_a = {x ∈ Rⁿ : ρ(x, E) ≤ a} is closed.

5 (Extension of a continuous function on a compact set). Assume K ⊂ Rⁿ is a compact set and f is a continuous function on K with 0 ≤ f (x) ≤ 1 for x ∈ K. Let

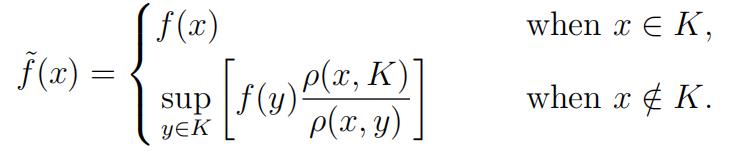
(i)Show that f˜(x) is continuous for x ∉ K.

(ii)Show that f˜(x)  is continuousfor x ∈ K. That is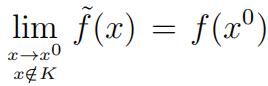

for any x0 ∈ ∂K.Here, ∂K denotes the boundary of K. Thus, (i) and (ii) together imply that f˜(x) is continuous on Rⁿ.

(iii)Show that 0 ≤ f˜(x) ≤ 1 for x ∈ Rⁿ.  初等实分析作业代写

(iv)Assumeg is a continuous and nonconstant function on K, denote

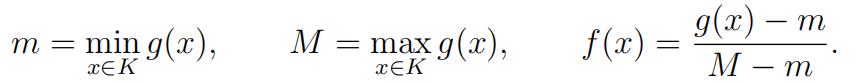
Using f (x) and parts (i)–(iii) to show that g(x) can be extended to a continuous function

g˜(x) on Rn   with m ≤ g˜(x) ≤ M .

(v)If a function h is continuous on an open set D ⊂ Rⁿ , is h always possible to be extended to a continuous function on Rn ? Consider the function h(x) = tan x for x ∈ (−π/2,π/2).

6(Mollifier). Consider the function  初等实分析作业代写

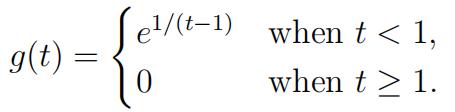
(i)Show that if a function φ(t) is defined in a neighborhood V_ϵ(t₀) and the limit lim φ^′(t) =l exists, then φ (t₀) exists and φ (t₀) = l.

(ii)Using part (i) to show that g ∈C^∞(R).

(iii) Let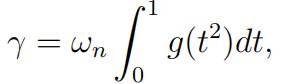where ωn is the surface area of the unit sphere in Rⁿ . Denote||x|| = (x²₁ + · · · + xx²_n)^1/2for x ∈ Rⁿ . Show that the function

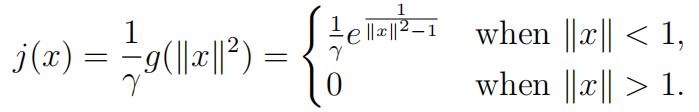
has the following properties

1) j(x) ≥ 0 for every x ∈ Rⁿ ; and j(x) = 0 when ∥x∥ ≥ 1;

2)

3)  j(x) ∈C₀^∞(Rn ).

Here, C₀^∞(A)  stands  for  the  set  of  smooth  functions  on  A  with  a  compact  support.   The support of a function is defined as

supp f = {x ∈ A ; f (x) 0} := the closure of the set where f does not vanish.  初等实分析作业代写

And if f  is smooth on A and supp f  is a compact subset of A, we write f  ∈ C₀^∞(A).

In what follows, we assume f is continuous on a compact K Rⁿ . By Problem 9, f can be extended to a continuous function on Rn , (we still denote this extension by f ). Define

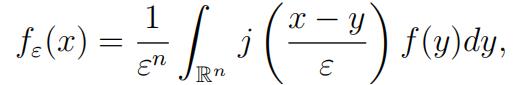(1)

which can be considered as the weighted average of f in the ball V_ε(x).

(iv)Show that f_ε(x) ∈ C^∞(Rⁿ).

(v)Show that,limε→0+f_ε(x) = f (x) uniformly for x ∈ K.

(vi)Redopart (iv) for an integrable function f on K: Assume f is integrable on K, and

extend f to Rn by setting f (x) = 0 for x / K. Show that, in this case, f_ε(x) defined in (1) also belongs to C0∞(Rⁿ ).

7 (Partition of unity).  初等实分析作业代写

(i)Assume K ⊂ U ⊂ Rn with K being nonempty compact and U open.Let

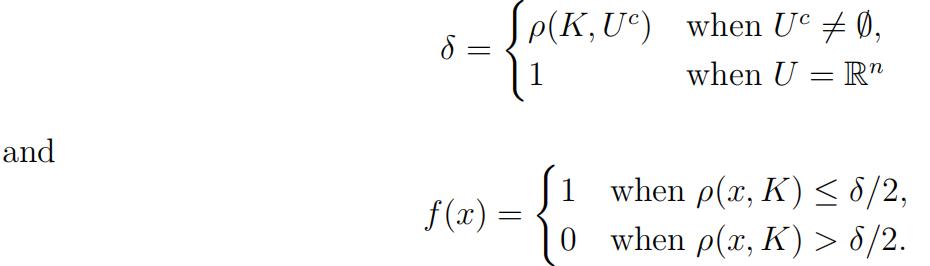
Here, ρ(x, K) is the distance of x to the set K as considered in Problem 8, and ρ(X, Y ) :=inf x∈X, y∈Y ρ(x, y) being the distance between two nonempty sets X and Y .

Let 0 < ε < δ/2. Show that f_ε(x) defined in (1) [as in Problem 10, part (vi)] satisfies

1)f_ε(x) = 1 when x ∈ K;

2)0 ≤ f_ε(x) ≤ 1 for all x ∈ Rⁿ;   初等实分析作业代写

3)suppf_ε ⊂ U .

(ii)Assume K ⊂ Rn is compact and U₁, . . . , U_Nis a finite open cover of K. Show that there exists another open cover V₁, . . . , V_N such that each V_j is bounded and V_j ⊂ U_j.

(iii)Assume K ⊂ Rn is compact and U₁, . . . , U_Nis a finite open cover of K. Show that

there exist functions h₁(x), . . . , h_N (x) such that

1) h_j(x) ∈ C^∞(Rn ) and supp h_j ⊂ U_j;

2)  h_j(x) ≥0;

N

3) 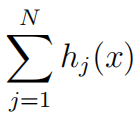= 1 for x ∈ K.

j=1

8. Letx,y Rⁿ and y = f (x) be a function. Recall that in the inverse theorem, one requires that f (x) to be C¹ near the point x⁰.  初等实分析作业代写

Consider the case n = 1 and

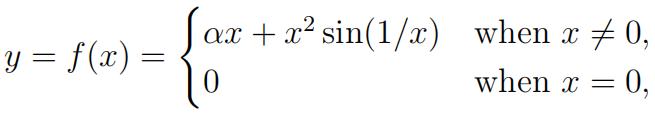
where 0 < α < 1.

(i)Findf^′(x) and show that f^′(x) is not continuous at 0.

(ii)Show that there are infinitely many points near x = 0 such that f ^′(x) = 0 and

f^′′(0)≠ 0, and thus conclude that there is no inverse function of y = f (x) near x = 0.

 

更多代写：美国assignment代写  多邻国代考  HIS作业代写  美国essay润色  马来西亚论文代写范文  代写演讲稿价格

合作平台：essay代写 论文代写 写手招聘 英国留学生代写