分析导论final代考 Final Exam代写

Introduction to Analysis

Final Exam

分析导论final代考 In the induction step, the original proof wrote “x and y were arbitrary pens in P so all pens in P are the same color”.

Problem 1 分析导论final代考

In the induction step, the original proof wrote “x and y were arbitrary pens in P so all pens in P are the same color”. Being arbitrary pens in P doesn’t imply x and y are of same color because P is an arbitrary set of n+1 pens, which is not proved to be of same color yet. The flaw in this proof provided is that it used the conclusion that we need to prove as an evidence.

Problem 2 分析导论final代考

(a)Suppose sets ,by definition. Note that if any one of them is not ℝ or ∅, then its complement is finite, and its union with another set whose complement is also finite would generate a new set whose complement is finite.

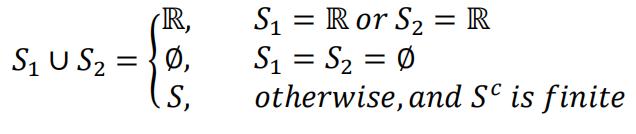
Therefore if 𝑆1, 𝑆2 ∈ 0, it follows that . For a countable union of sets in 0, we have, by induction, the union is also in 0

(b)Suppose ,we have that:

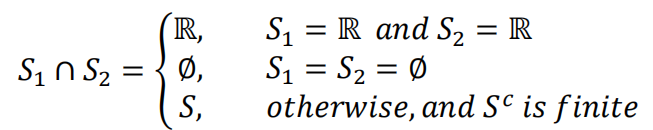
The third scenario can be proved by showing:

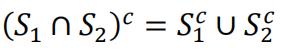
Is a union of two finite sets. It’s obvious is also finite. By induction, a union of finite number of finite sets is also finite. Therefore a finite intersection of sets in is also in 0. 分析导论final代考

(c)Proof: for every element 𝑂 ∈ 0 that contains 0, then 𝑂 = ℝ or that is finite by definition of 0. If 𝑂=ℝ, then there exists that for all 𝑛 ≥ 100.

If is finite and𝑂≠ℝ, then there exists 100 ∈ ℕ a finite set of points {𝑑1,𝑑2,… ,𝑑𝑘|𝑑𝑖∈ℝ, 𝑑𝑖∉𝑂} that i𝑛∈𝑂=ℝis not in . Without loss of generality assume is the minimum of these points with a positive value. Then we have 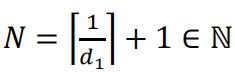, such that 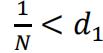. For any 𝑛 ≥ N, 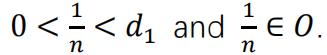If such positive 𝑑1 doesn’t exist, then let N = 100.

So 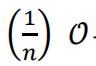-converges to 0. 分析导论final代考

(d)Following the routine in part (c). Note that if 𝑂 = ℝ that contains 1, then𝑁 = 100, for all𝑛 ≥100, .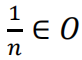

If is finite and 1∈0. Because 𝑂c is finite, so 𝑂 must contain an interval that has 0 in it. We can still have 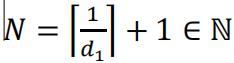where 𝑑1 is the smallest positive value in the point set that is not in 𝑂. And for all 𝑛 ≥ N,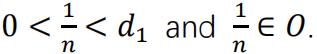

The above argument can be further expanded to prove that sequence 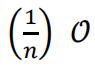-converges to any 𝐿 ∈ ℝ.

(e)Prove: for any 𝐿∈ℝ,if and𝑂∈0, then𝑂=ℝ or 𝑂𝑐 is finite

If 𝑂=ℝ, let 𝑁=100, for any 𝑛≥100,𝑥𝑛=𝑛∈ 𝑂.

If , note that only a finite set of k points is not in , let be the maximum value of such points, and 𝑁=⌈𝑑𝑘⌉ +1∈ℕ. For any 𝑛≥N，𝑥𝑛=𝑛 >𝑑𝑘, 𝑥𝑛 ∈ 𝑂.

Therefore (𝑛) 0 -converges to any 𝐿 ∈ ℝ

Problem 3 分析导论final代考

(a)With , the derivative of f is:

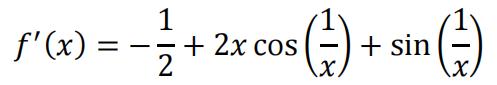
When x = 0, the derivative is:

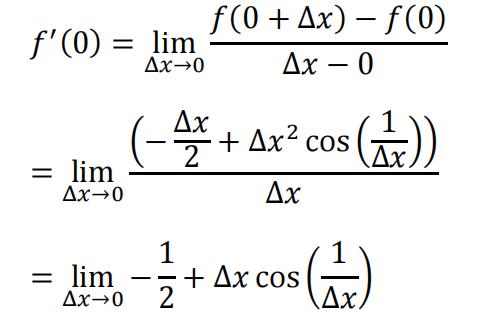
Because for any , so:

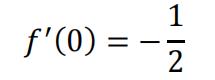
Therefore, f(x) is differentiable on , and that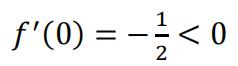

(b)In an open interval that contains 0:

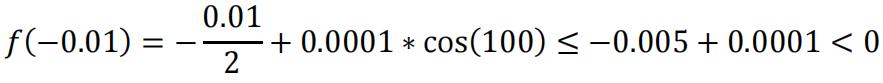
And 𝑓(0) = 0

Therefore there must be an open interval containing both 𝑥 = −0.01 and 𝑥 = 0 that f(x) is not decreasing.

Problem 4 分析导论final代考

(a)Regardless of the enumeration scheme of ℚ,there is always a one-to-one mapping between ℕ and ℚ. Without loss of generality, assume that there is a subset 𝑋𝑁 ⊂ ℕ such that if 𝑛∈ 𝑋N, then 𝑞𝑛 < x. Now for any 𝜖> 0:

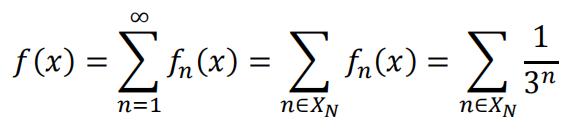
Note that , so we can find a smallest N such that 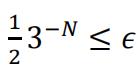, and:

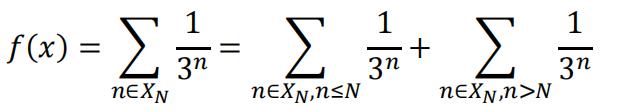
The first part is finite, the second part ≤∈. So it’s obvious that 𝑓(𝑥) is finite and well-defined for all 𝑥 ∈ ℝ.

(b)Suppose and 𝑦 > x and𝑥, 𝑦∈ ℝ,then there must be a subset and a subset 𝑌𝑁 ⊂ ℕ such that if , and if 𝑛 ∈ 𝑌𝑁, 𝑞𝑛 < y. Since if 𝑞𝑛 <x, then 𝑞𝑛 < y.

Rationales are dense, so in the interval , there must be at least one 𝑁∗ that 𝑥< 𝑞𝑁∗ <y. And 𝑁∗ ∈ 𝑌𝑁, 𝑁∗ ∉ 𝑋N

We have:

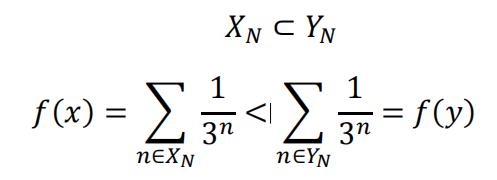
So f(x) is monotone.

(c)Suppose 𝑥∈ ℚ,then there exists 𝑁∗ that𝑞𝑁∗ = x. For any 𝜖> 0, in the interval of(𝑥 − 𝜖, 𝑥), there must be a subset 𝜖𝑁 ⊂ℕ that if𝑛 ∈𝜖𝑁,𝑞𝑛 ∈(𝑥 −𝜖, 𝑥).

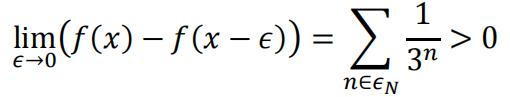
Therefor𝑓(𝑥) is discontinuous at all 𝑥 ∈ ℚ.

Problem 5

(a)The antiderivative of the Weierstrass function is:

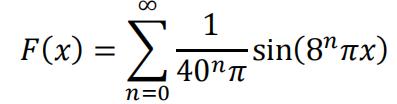
Both 𝐹(𝑥) and 𝑓(𝑥) is continuous on ℝ and𝐹(𝑥) is differentiable with 𝐹′(𝑥) = 𝑓(𝑥).

By the fundamental theorem of calculus,𝑓(𝑥) is integrable.

(b)The function is found in part (a):

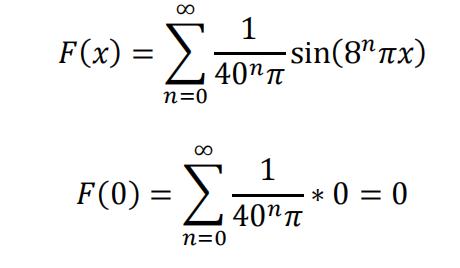
(c)By definite integral:

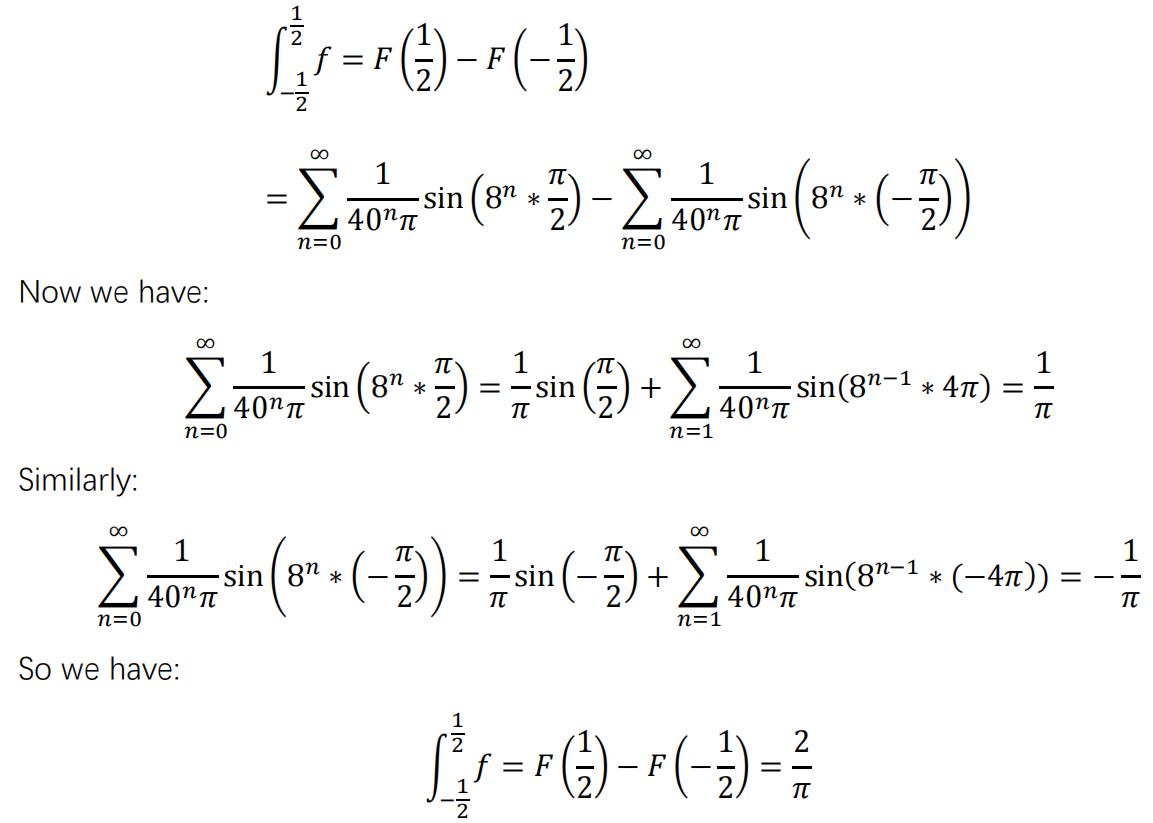
Problem 6

(a)Prove:

When 𝑥′ = 𝑥” ∈ [𝑥]

𝑑([𝑥],[])=inf{|𝑥′−𝑥”|:𝑥′∈[𝑥],𝑥”∈[𝑥]}=0

And for any 𝑥, 𝑦 ∈ 𝑋:

𝑑([𝑥],[𝑦]) =inf{|𝑥′−𝑦′|: 𝑥′∈[𝑥], 𝑦′∈[𝑦]}=inf{|𝑦′−𝑥′|:𝑥′∈[𝑥],𝑦′∈[𝑦]}

=𝑑([𝑦],[𝑥])

For any𝑥, 𝑦, 𝑧∈X

𝑑([𝑥],[𝑧])=inf{|𝑥′−𝑧′|:𝑥′ ∈[𝑥], 𝑧′ ∈[𝑧]} 分析导论final代考

≤inf{|𝑥′−𝑦′|+|𝑦′−𝑧′|: 𝑥′∈[𝑥], 𝑦′ ∈[𝑦], 𝑧′ ∈[𝑧]}

≤inf{|𝑥′−𝑦′|:𝑥′∈[𝑥],𝑦′ ∈[𝑦]} +inf{|𝑦′−𝑧′|: 𝑦′ ∈[𝑦], 𝑧′ ∈ [𝑧]}

≤𝑑([𝑥],[𝑦])+𝑑([𝑦],[𝑧])

therefore𝑑([𝑥],[𝑦]) is a valid metric on the set of equivalence classes of this relation.

(b)The value of can be calculated by definition:

𝑑([𝜋],[1000]) = inf{|𝑥′ −𝑦′|: 𝑥′ ∈ [𝜋], 𝑦′∈ [1000]}

Now the equivalence relation is given by 𝑥~𝑥′ if 𝑥− 𝑥′ ∈ ℤ

So [𝜋] = {𝑥 + 𝜋|𝑥 ∈ ℤ}, [1000] =ℤ, and it’s easy to verify that:

𝑑([𝜋],[1000]) = 3.14 − 3 = 0.14

Problem 7 分析导论final代考

(a)By definition:

𝑑∞((𝑥𝑛), (𝑦𝑛)) =sup{||sin(𝑛 −1)| − |cos(𝑛 −1)||: 𝑛∈ℕ}

Now to maximize|sin(𝑛−1)|− |cos(𝑛 − 1)|, we can assume that for a proper n,

sin(𝑛−1)→1andcos(𝑛−1)→0at the same time, i.e.𝑛−1→2𝑘𝜋+ 𝜋2 for some𝑘∈ℤ

Now to maximize , we can assume that for a proper n, and at the same time, i.e. for some 𝑘∈ℤ. 分析导论final代考

And𝑑∞((𝑥𝑛),(𝑦𝑛)) = 1

(b)A sequence in(𝑥𝑛)i is Cauchy ℓ∞if for every 𝜖>0, there exists 𝑁 ∈ ℕ such that whenever , then

𝑑∞((𝑥𝑛)𝑎,(𝑥𝑛)𝑏)=sup{|𝑥𝑛𝑎− 𝑥𝑛𝑏|:𝑛∈ℕ, 𝑥𝑛𝑎 ∈ (𝑥𝑛)𝑎,𝑥𝑛𝑏∈(𝑥𝑛)𝑏} < 𝜖

Now that(𝑥𝑛)i 𝑖s bounded for any i, then we must have a converging subsequence of(𝑥𝑛)𝑖 . Let (𝑥𝑛)𝑝𝑖denote the subsequence, and 𝑝𝑖 lim→∞(𝑥𝑛)𝑝𝑖 be the limit. For any 𝜖 > 0,

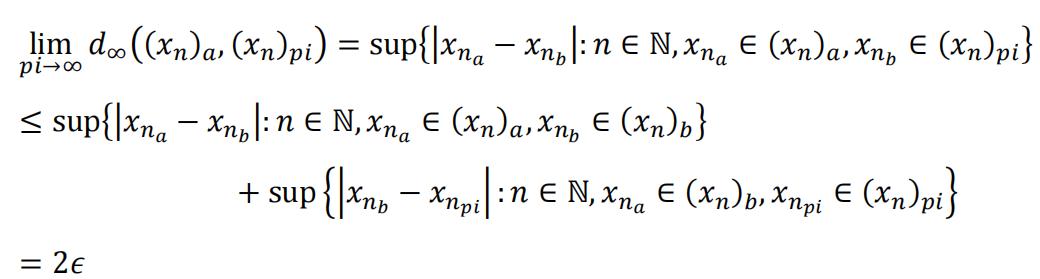
With 𝑎, 𝑏 ≥𝑁, and(𝑥𝑛)b

is in the converging subsequence. So Cauchy sequences in ℓ∞ converges. And

(ℓ∞,𝑑∞((𝑥𝑛),(𝑦𝑛)))is a complete metric space.

合作平台：essay代写论文代写写手招聘英国留学生代写