Final
分析导论代考 In the induction step, the original proof wrote “x and y were arbitrary pens in P so all pens in P are the same color”.
Problem 1
In the induction step, the original proof wrote “x and y were arbitrary pens in P so all pens in P are the same color”. Being arbitrary pens in P doesn’t imply x and y are of same color because P is an arbitrary set of n+1 pens, which is not proved to be of same color yet. The flaw in this proof provided is that it used the conclusion that we need to prove as an evidence.
Problem 2 分析导论代考
(a)Suppose sets ![]() ,by definition. Note that if any one of them is not
,by definition. Note that if any one of them is not ![]() or ∅, then its complement is finite, and its union with another set whose complement is also finite would generate a new set whose complement is finite.
or ∅, then its complement is finite, and its union with another set whose complement is also finite would generate a new set whose complement is finite.
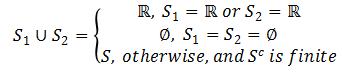
Therefore if ![]() , it follows that
, it follows that ![]() . For a countable union of sets in
. For a countable union of sets in ![]() , we have, by induction, the union is also in
, we have, by induction, the union is also in![]()
(b)Suppose 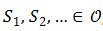 ,we have that:
,we have that:
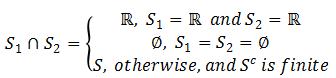
The third scenario can be proved by showing:
![]()
Is a union of two finite sets. It’s obvious ![]() is also finite. By induction, a union of finite number of finite sets is also finite. Therefore a finite intersection of sets in
is also finite. By induction, a union of finite number of finite sets is also finite. Therefore a finite intersection of sets in ![]() is also in
is also in ![]()
(c)Proof: for every element ![]() that contains 0, then
that contains 0, then ![]() or that
or that ![]() is finite by definition of
is finite by definition of ![]() . If
. If ![]() , then there exists
, then there exists ![]() for all n ≥100.
for all n ≥100.
If ![]() is finite and
is finite and ![]() , then there exists a finite set of points
, then there exists a finite set of points ![]()
![]() that is not in 0. Without loss of generality assume d1 is the minimum of these points with a positive value. Then we have
that is not in 0. Without loss of generality assume d1 is the minimum of these points with a positive value. Then we have ![]() , such that
, such that ![]() . For any
. For any ![]() , and
, and ![]() . If such positive doesn’t exist, then let N = 100.d1
. If such positive doesn’t exist, then let N = 100.d1
So ![]() -converges to 0.
-converges to 0.
(d)Following the routine in part (c). Note that if![]() that contains 1, then N = 100, for all n≥100,
that contains 1, then N = 100, for all n≥100, ![]() . 分析导论代考
. 分析导论代考
If ![]() is finite and 1∈0 . Because
is finite and 1∈0 . Because ![]() is finite, so 0 must contain an interval that has 0 in it. We can still have
is finite, so 0 must contain an interval that has 0 in it. We can still have ![]() where d1 is the smallest positive value in the point set that is not in 0. And for all
where d1 is the smallest positive value in the point set that is not in 0. And for all ![]() .
.
The above argument can be further expanded to prove that sequence ![]() -converges to any
-converges to any ![]() .
.
(e)Prove: for any ![]() ,if
,if ![]() , then
, then ![]() is finite
is finite
If ![]() , let N = 100, for any n = 100,
, let N = 100, for any n = 100, ![]() .
.
If ![]() ,L∈0 note that only a finite set of k points is not in , let dk be the maximum value of such points, and
,L∈0 note that only a finite set of k points is not in , let dk be the maximum value of such points, and ![]() . For any
. For any![]()
![]() .
.
Therefore -converges to any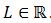 .
.
Problem 3
(a)With x≠0, the derivative of f is:
![]()
When x = 0, the derivative is:
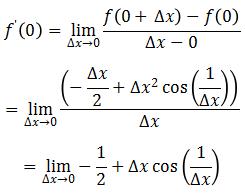
Because cos(x)∈[-1,1] for any ![]() , so:
, so:
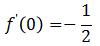
Therefore, f(x) is differentiable on , and that ![]()
(b)In an open interval that contains 0:
![]()
And f(0)=0
Therefore there must be an open interval containing both and that f(x) is not decreasing.

Problem 4
(a)Regardless of the enumeration scheme of Q,there is always a one-to-one mapping between N and Q. Without loss of generality, assume that there is a subset ![]() such that if
such that if ![]() , then
, then ![]() . Now for any
. Now for any ![]() :
:
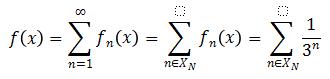 <
<
Note that ![]() , so we can find a smallest N such that
, so we can find a smallest N such that ![]() , and:
, and:
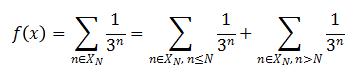
The first part is finite, the second part ≤∈. So it’s obvious that f(x) is finite and well-defined for all ![]() .
.
(b)Suppose y>xand y,x∈R, then there must be a subset YN ⊂N and a subset XN⊂N
such that if ![]() , and if
, and if ![]() . Since if
. Since if ![]() , then qn<y.
, then qn<y.
Rationales are dense, so in the interval (x,y)≠Ø, there must be at least one N*that ![]()
We have:
![]()
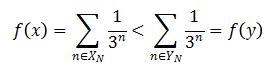
So f(x) is monotone.
(c)Suppose ![]() ,then there exists N* that
,then there exists N* that ![]() . For any
. For any ![]() , in the interval of
, in the interval of ![]() , there must be a subset
, there must be a subset ![]() that if
that if ![]() .
.
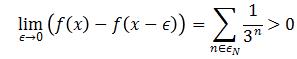
Therefore f(x) is discontinuous at all x∈R.
Problem 5 分析导论代考
(a)The antiderivative of the Weierstrass function is:
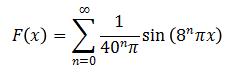
Both F(x) and f(x) is continuous on R and F(x) is differentiable with F(x)=f(x).
By the fundamental theorem of calculus, f(x) is integrable.
(b)The function is found in part (a):
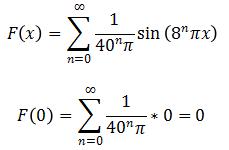
(c)By definite integral:
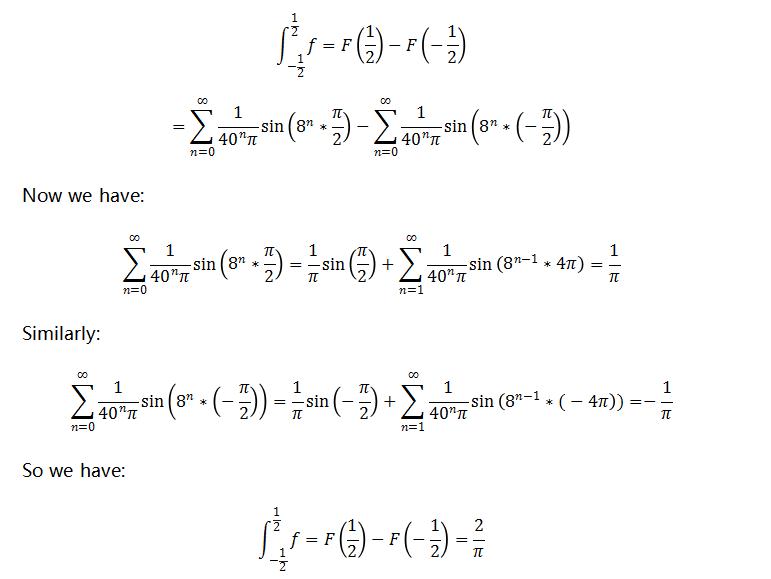
Problem 6
(a)Prove:
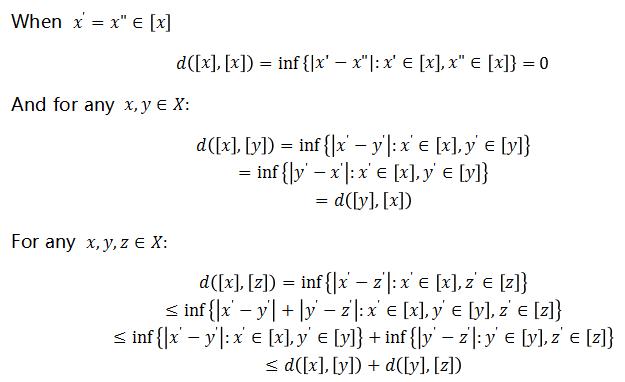
therefore d([x],[y]) is a valid metric on the set of equivalence classes of this relation.
(b)The value of d([π],[1000]) can be calculated by definition:
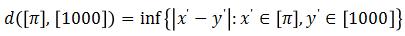
Now the equivalence relation is given by if![]()
So ![]() and it’s easy to verify that:
and it’s easy to verify that:
![]()
Problem 7 分析导论代考
(a)By definition:
![]()
Now to maximize ![]() , we can assume that for a proper n, sin(n-1)→1 and sin(n-1)→0 at the same time, i.e.
, we can assume that for a proper n, sin(n-1)→1 and sin(n-1)→0 at the same time, i.e. ![]() for some
for some ![]() .
.
And ![]()
(b)A sequence ![]() in
in ![]() is Cauchy if for every
is Cauchy if for every ![]() , there exists
, there exists ![]() such that whenever
such that whenever ![]() , then
, then ![]()
(c)Assume that sequence ![]() is Cauchy in
is Cauchy in ![]() , then for every
, then for every ![]() , there exists
, there exists ![]() such that whenever
such that whenever ![]() , then:
, then:
![]()
Now that ![]() is bounded for any i, then we must have a converging subsequence of
is bounded for any i, then we must have a converging subsequence of ![]() . Let
. Let ![]() denote the subsequence, and
denote the subsequence, and ![]() be the limit. For any ∈>0, we
be the limit. For any ∈>0, we
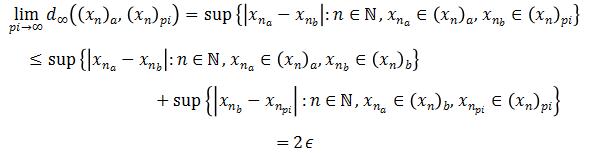
With a,b<N and ![]() is in the converging subsequence. So Cauchy sequences in
is in the converging subsequence. So Cauchy sequences in ![]() converges. And
converges. And ![]() is a complete metric space.
is a complete metric space.

