分地域地对我国原保险保费的阐明和预测
改良开放以来,中国的保险业经验了三十多年的高速增长,在赔偿灾害损失、维护社会安宁、支持中国的经济建树等方面发挥了重要浸染,具有辽阔的成长前景和潜力。跟着中国保险业进入深化改良、全面开放、加速成长的新阶段,保险业处事经济社会的规模越来越广,包袱的社会责任越来越重,保险业正在尽力提高科学成长和处事经济社会全局的本领。这就要求保险行业能有效地举办成长筹划。个中,原保费收入是权衡保险业成长的重要指标之一,对其举办精确的阐明和实时的预测对行业打算的拟定来说很是重要。
可是,我国经济成长不服衡,导致保险行业成长不服衡。假如只是对全国原保险保费举办阐明和预测,显然不能指导有针对性的打算拟定。于是,我们按照的2012年2月全国各地域(省级行政单元)的原保险保费收入数据,对各个地域举办聚类,再有代表性地分地域举办保费收入阐明和预测。
首先按照数据(见附录1)举办地域的聚类。思量到人口是保费收入的显著影响因素,于是操作2010年全国人口普查数据对原数据做人均处理惩罚,并综合各聚类要领得出以下聚类功效:
数据剪影(人均):
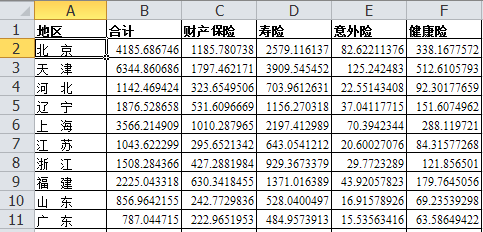
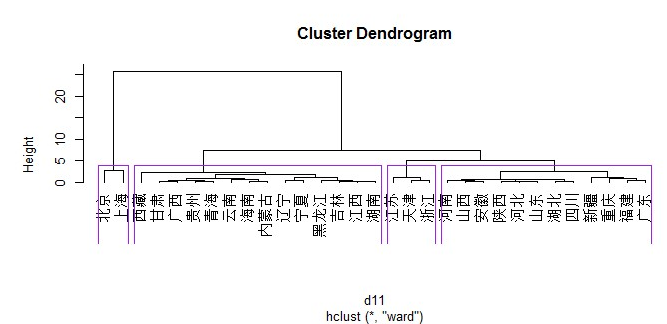
第一类:北京,上海;
第二类:江苏,天津,浙江;
第三类:河南,山西,安徽,陕西,河北,山东,湖北,四川,新疆,重庆,福建,广东;
第四类:西藏,甘肃,广西,贵州,青海,云南,海南,内蒙古,辽宁,宁夏,黑龙江,吉林,江西,湖南。
分类的功效根基切合我们的直观感觉,经济发家的处所保险业也较发家,人们的保险意识相对较强。
接下来,我们从这四类中别离随机抽取一个地域作为代表,再举办保险保费预测。
随机抽取功效如下:

我们将团结学过的常识,操作以上四个地域2006年1月–2012年2月原保险保费收入的原始数据,举办多方面的阐明,虽然会把重点放在原保险保费的预测上。由于研究要领一致,所以我们只将第一类代表——上海的探究进程具体论述,其它三个地域的则只给出功效。
@上海市原保险保费收入数据阐明和预测
1. 总体阐明
原始数据剪影如下:
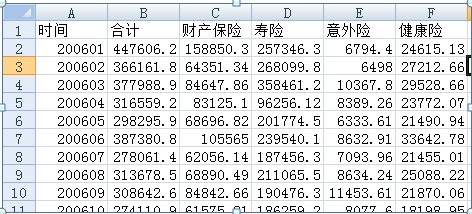
通过画图、成立回归模子等方法对数据作劈头的阐明处理惩罚。
1.1 通过pairs()查察数据各列之间的二元图
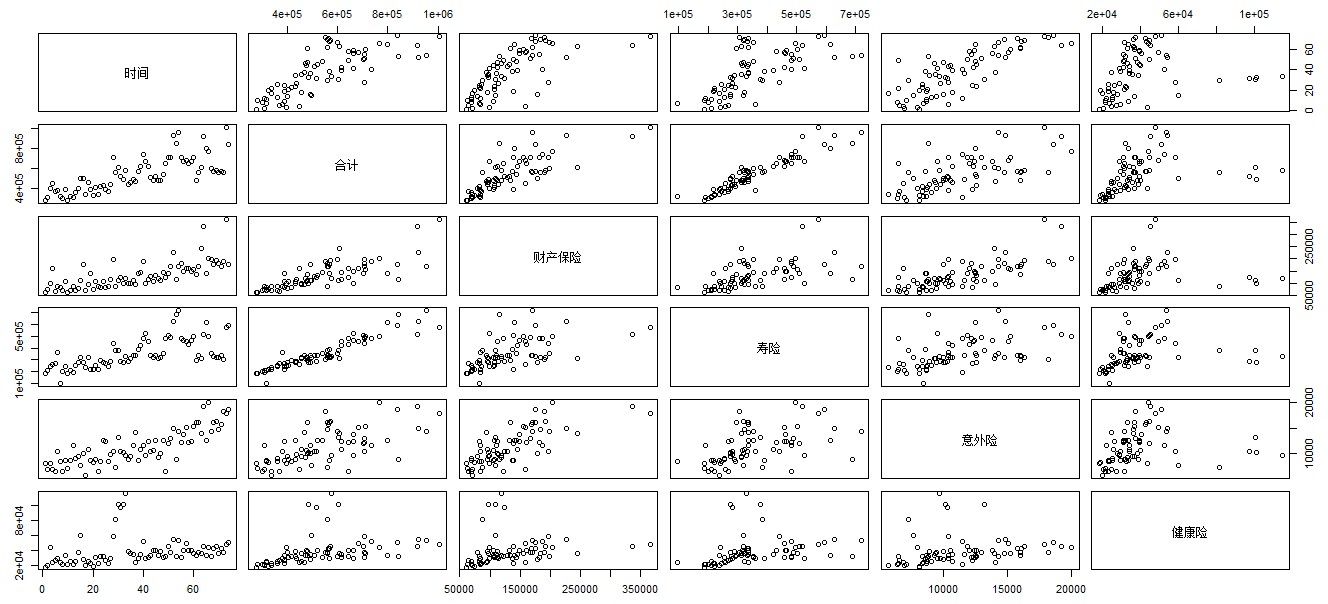
从上图可以看出,保险总收入随时间推移大抵呈增长状况,这和我们平时的直观认识相符。别的,差异险种之间好像存在必然水平的线性相关。
1.2 阐明差异险种之间大概存在的干系
1.2.1 主身分分类
对样本作主身分分类,绘制结果图如下(1、2、3、4别离对应工业保险、寿险、意外险和康健险):
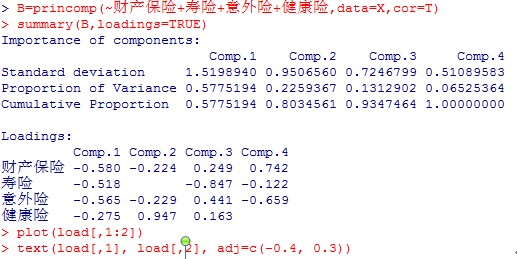
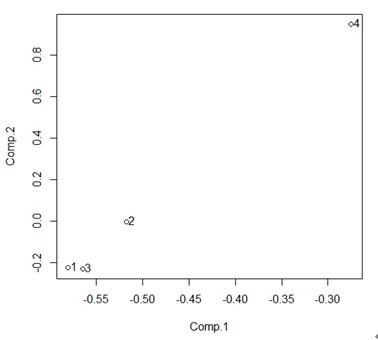
从图中看生工业保险和意外险可当作一类,寿险和康健险各成一类。对此作出一个大概的表明是:购置工业保险一般是源于制止受到意外的工业损失,这种意外很大比例是由自然灾害或其他意外变乱造成,这些变乱一旦产生,将有很或许率对人自身造成意外伤害,所以工业保险和意外险经常是一并购置的。
1.2.2 主身分回归
以工业保险为相应变量,研究工业保险和其他险种的线性干系,先成立模子,再用主身分阐明法举办模子批改。全进程如下:
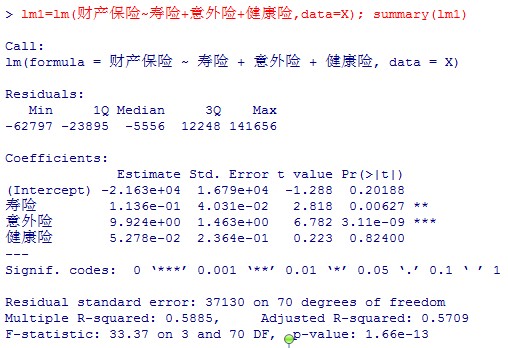
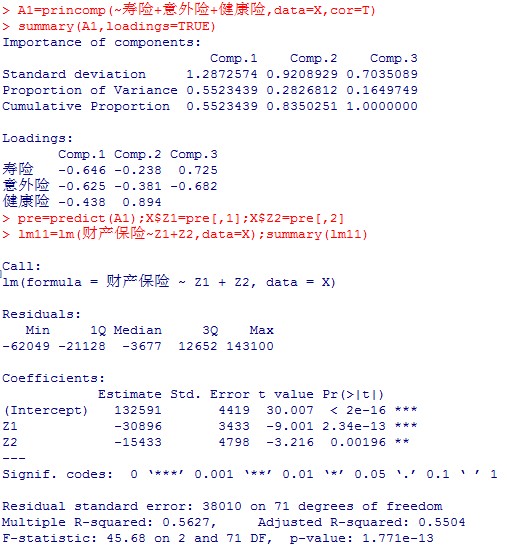
用同样的要领成立以其他险种为响应变量的回归模子,发明同样的特点:R方的值并不抱负,可是显著性较强。团结pairs()的二元图,我们猜测差异险种之间确实有必然水平的线性相关,可是受其他因素的影响,可是这种线性相关不敷以用线性表达式完全表达。
2. 部门阐明
画图阐明每一年内保费总收入变革环境如下:
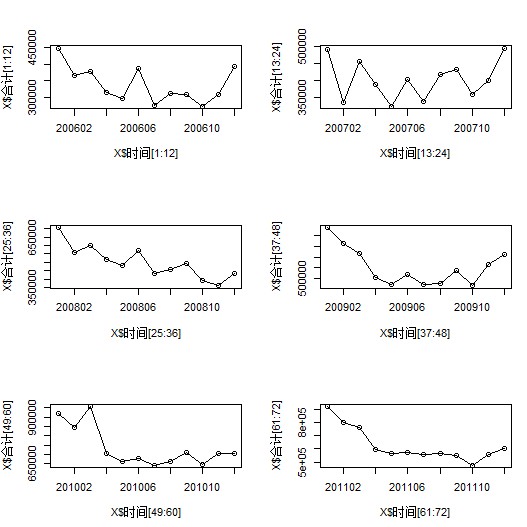
各年各月保费收入大抵存在以下纪律:1月份保费较高,随后递减,6月份呈现新的小岑岭,随后继承递减,10月份后又开始递增,这大概与内地的政策、保险公司推出的新产物、人们的消费习惯、其时从业人员的数量等等有关。
由于保费收入具有很强的关于时间的周期性特征,可以思量利用ARIMA模子做关于保费收入合计的时间序列预测。对付保险规模以致经济金融规模里与时间序列有关的指标,都可以操作ARIMA模子做出较正确的短期预测,从而指导行业的成长筹划。
3. 数据预测
3.0关于ARIMA模子的简介
ARIMA模子全称为差分自回归移动平均模子(Autoregressive Integrated Moving Average Model,简记ARIMA),是由博克思(Box)和詹金斯(Jenkins)于70年月初提出的一著名时间序列预测要领,所以又称为box-jenkins模子、博克思-詹金斯法。个中ARIMA(p,d,q)称为差分自回归移动平均模子,AR是自回归,p为自回归项;MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。
可能说,所谓ARIMA模子,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值举办回归所成立的模子。ARIMA模子按照原序列是否平稳以及回归中所含部门的差异,包罗移动平均进程(MA)、自回归进程(AR)、自回归移动平均进程(ARMA)以及ARIMA进程。
3.1 绘制趋势线、自相关、偏自相关图
趋势线:ts.plot(Insurance)
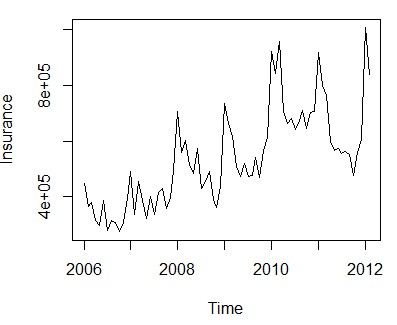
自相关图:acf(Insurance)
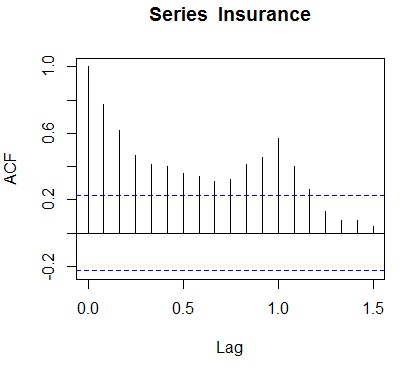
偏相关图:pacf(Insurance)
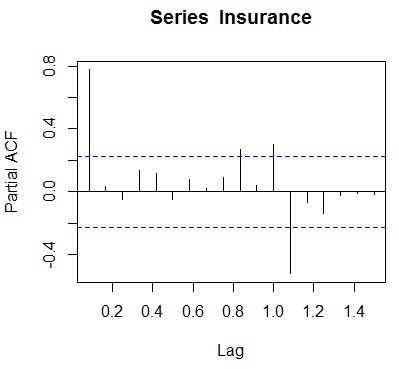
劈头判定有趁势、季候性,将其用decompose函数举办解析:
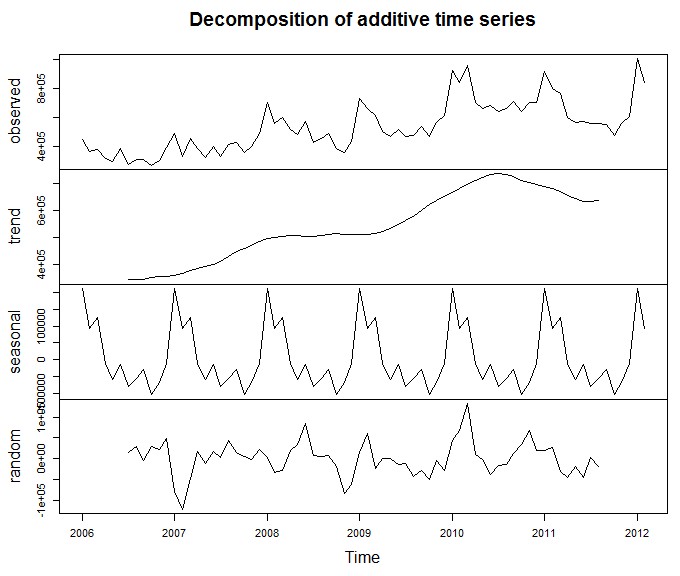
3.2成立模子
用auto.arima()自动生成arima最优拟合模子的参数,Insurance.fit即为生成的模子:
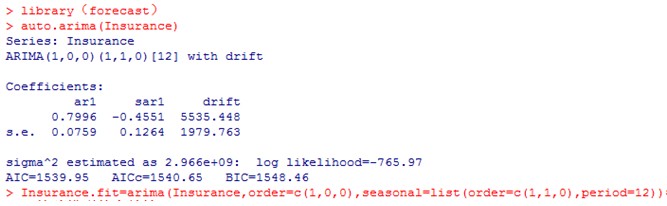
用tsdiag()检讨模子的有效性:

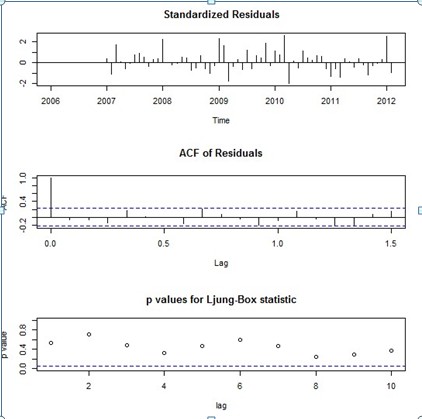
第二行的ACF检讨说明残差没有明明的自相关性。第三行的Ljung-Box 测试显示所有的P-value>0.1,说明残差为白噪声。模子及格。
3.3 数据预测
下面举办一年时间的保费预测,给出80%(黄色),95%(橙色)置信度下的置信区间,
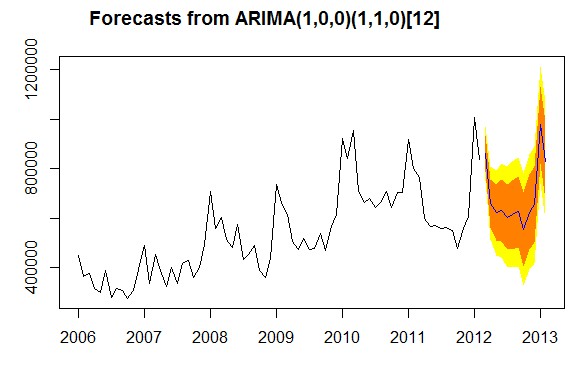
预测出的数据如下:
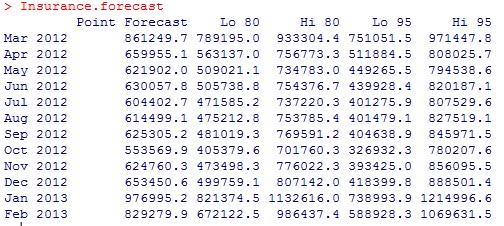
按照预测的数据,保险公司可以当令调办理策偏向、推出新产物。值得说明的是,尽量给出了将来12个月的预测值,只有短期的预测值有较大参考代价。从恒久来看,由于影响不确定性因素增加,模子的预测本领必会下降。
@江苏省原保险保费收入数据阐明和预测
江苏的环境与上海的存在差别。
下面是对四个险种(1:工业保险;2:人寿保险;3:意外险;4:康健险)举办主身分分类的功效。
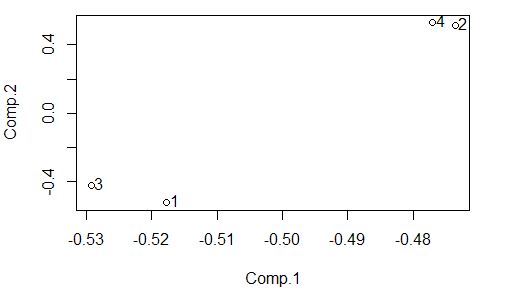
从图中看生工业保险和意外险是一类,寿险和康健险是一类。对此作出的一个表明是:买寿险的江苏人会对自身康健程度较量存眷,所以两种保险存在很强的相关干系;工业保险和意外险分类环境与上海大抵沟通,购置工业保险一般是源于制止受到意外的工业损失,这部门人所糊口和事情的情况大概就是他们的工业地址地,也不免碰着意外,所以工业保险和意外险经常是一并购置的。
而对江苏保费收入举办预测时,我们发明江苏省原保险保费数据明明地呈周期增长趋势,原数据颠簸较大(如下左图所示),可以先对数据举办预处理惩罚,这里对数据取自然对数(如下右图所示),使数据相对的平缓。
趋势线:ts.plot(Total) ts.plot(lntotal)
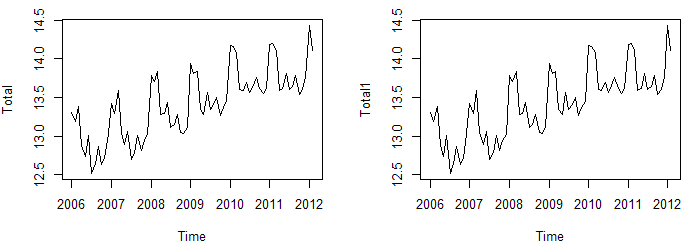
操作Arima函数举办模子构建,我们发明做这样的预处理惩罚可以令模子更让人满足。
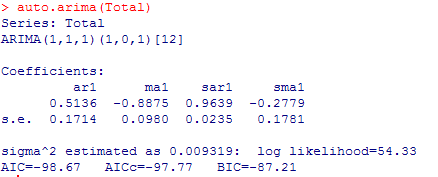
Sigma^2 estimated 的值较小,并且ar1~sma1呈现负值。
预测功效如下:
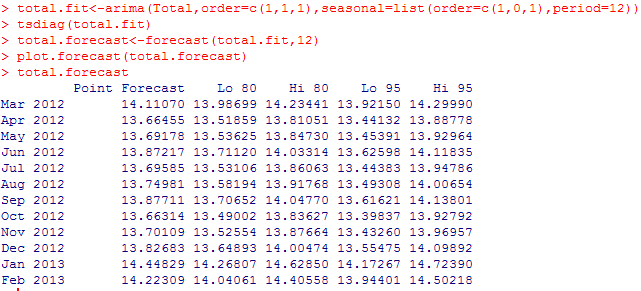
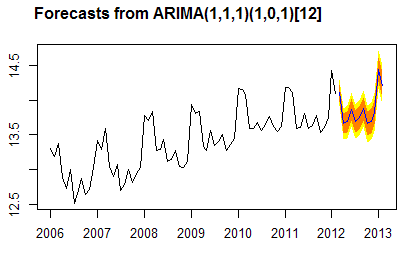
获得功效之后再举办数值调动即可。
@广东省原保险保费收入数据阐明和预测
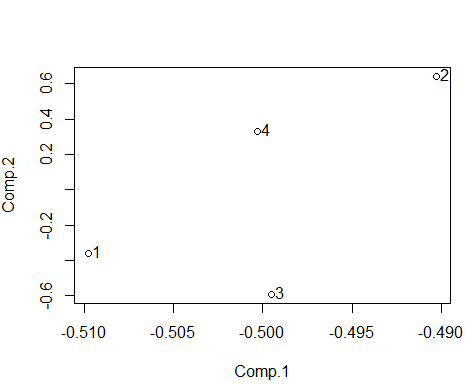
由图上看出各个险种间并无明明干系,为四个彼此独立的种别,由此得出广东人在选择购置的保险种类时对各险种的选择相对来说较量地独立。
保费收入预测:
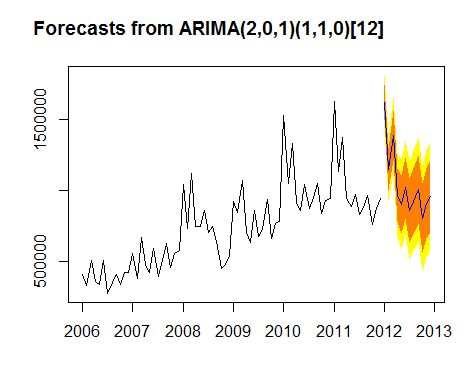
@云南省原保险保费收入数据阐明和预测
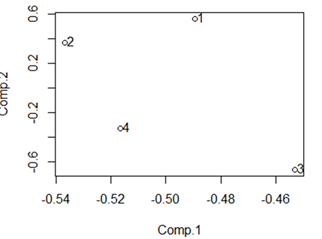
从图中可以看出,四个险种各成一类,阐明:在云南省,人们买保险,各个险种之间是无明明相关干系。
保费收入预测:
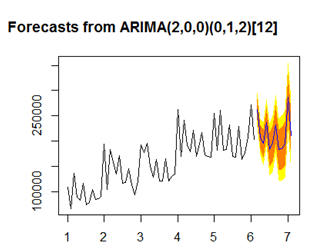
从以上的探究我们可以得出几个结论:
1. 差异地域人们的消费习惯等影响了保险购置的行为,各大保险公司在举办业务打算时应因地制宜,按照差异的地域的环境做出差异的决定,设计差异的险种可能掘客差异的销售方法,以助于提高收入;
2. 各地域代表的保费收入依然呈周期增长趋势,保险行业有强劲的成长趋势,各保险公司可以按照这个短期的预测拟定成长打算以及相关险种的销售打算等,有利于其成长壮大。
