递归在编程中的意思就是程序调用自身的技巧。也可以说是函数在定义中使用函数自己。就像Hanoi游戏一样,解决的方法也是使用了递归的思想不断地调用同一种解决的方法。C中还有一种思想叫迭代,和递归思想相类似,下面我们来了解一下递归和迭代。
递归概念
程序在调用一个函数的过程中出现直接或者间接的调用函数本身,这就是递归。在C语言编程中总会遇到规模较大的问题,这时候我们就可以将它分解成很多的小问题,然后从小问题的解构造出大问题的解。不过要在递归中设定递归的条件。不然就是死循环。
迭代概念
不断重复反馈的过程,目的是为了逼近所需目标或者结果。每一次对过程的重复称为一次”迭代”,迭代的结果将作为下一次迭代的值。
两者的区别
迭代使用的是循环结构,递归使用的选择结构(选择结构用于判断给定的条件,根据判断的结果判断某些条件,根据判断的结果来控制程序的流程)。但是要注意任何递归能解决的问题迭代都能解决。
两者的优点
迭代不需要反复调用函数和占用额外的内存(对于递归来说,大量的递归会占用大量的内存,因为每一次的递归调用都会建立函数备份)。递归能是程序的结构更加清晰,让人更加容易理解。
递归有一个经常用于讲解的问题:Hanoi 塔问题
有三个柱子A、B、C,A中有诺干个圆盘,大小没有相等的。而且小的在上打的在下,你需要把这诺干个圆盘移动到C中,每次只能移动一个,而且一定要保证小的在上,大的在下。
我们来解决一个简单的Hanoi 塔问题,在Hanoi 塔中只有三个盘子。
说个题外话:
我在网上看到有朋友做个一个计算。如果有n个盘子,则总的移动所需次数为2的n次方-1;那如果我说,盘数有64个,你会觉得大吗?我们来算一下:2^64 – 1 = 18446744073709551615 。为5.05390248594782e+16年,也就是约5000世纪,如果对这数字没什么概念,就假设每秒钟搬一个盘子好了,也要约5850亿年左右。所以你能想到就64个盘子都要用5850亿年来搬么。
看完64个盘子我们来分析3个盘子的Hanoi问题。
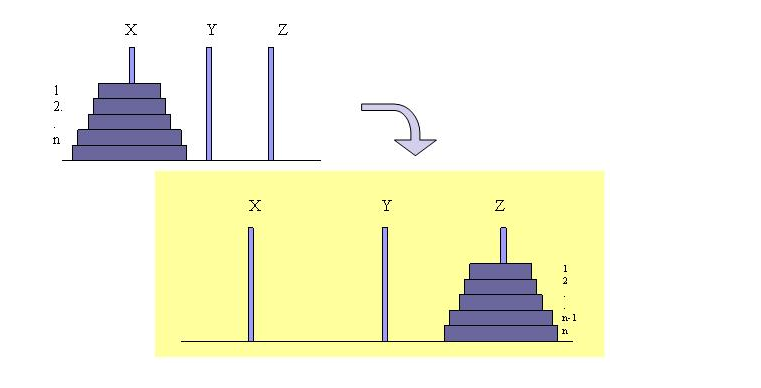
有一个简单的解法:A、B、C排列成一个三角形,A->B->C->A构成一顺时针循环。在移动圆盘的过程中,若是奇数次移动,则将最小的圆盘移到顺时针方向的下一塔座上;若是偶数次移动,则保持最小的圆盘不动。而其他两个塔座之间,将较小的圆盘移到另一塔座上去。
如果你觉得3个圆盘太简单,你可以用此方法对4个圆盘的Hanoi进行运算,你会惊奇的发现这个问题如此简单。
用递归来解决:
当n=1的时候,将最小的1移至B塔。
当n>1的时候,需要利用塔座C作为辅助塔座。此时设法将n-1个较小的圆盘依照移动规则从塔座A移至塔座C,然后,将剩下的最大圆盘从塔座A移至塔座B,最后,再设法将n-1个较小的圆盘依照移动规则从塔座C移至塔座B。
这样子n个圆盘的移动问题就变成了两次n-1个圆盘问题,这样我们就可以对它进行递归的运算。

如果你看完Hanoi问题还不是很懂,我们再看一个递归求 3的阶乘:
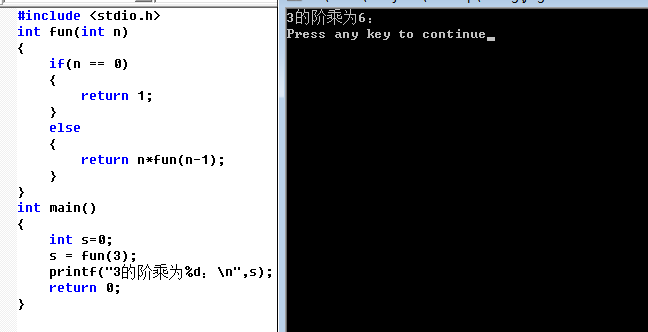
用迭代的方法算一次:
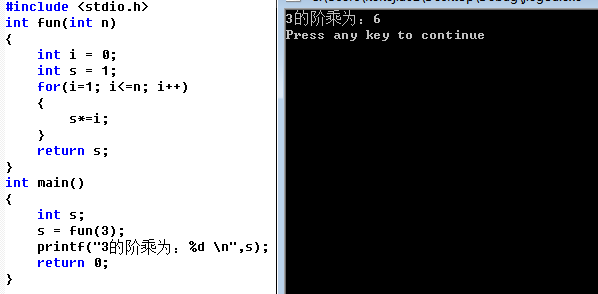
递归的用法看完你可能知识了解了概念和作用,但是真正运用的时候回觉得难以下手。所以你应该自己设计一个简单的递归程序,自己在纸上写出程序的过程,再去慢慢的理解。这样子会对你理解递归很有帮助。
