AMATH 342 Fall 2019: Assignment 4
Fourier analysis代写 Assignments below are either theory or computational. For the computational assignments you may use any programming language
Office hrs: Monday’s 11:00-12:00, MC 6134
Due Date: Tuesday 3 December, 2019, before midnight
Total points: 39. Your grade will be in terms of a percentage (rounded to the nearest integer).Fourier analysis代写
Assignments below are either theory or computational. For the computational assignments you may use any programming language you want except Maple or Mathematica. Please hand in a single document that includes: (i) all responses to the exercises, (ii) all figures (if asked) (iii) all codes. You can either print everything and give it to the instructor, or include everything in a single pdf file and email it to the TA and to the instructor.
1.Consider the advection equation:Fourier analysis代写
∂tu + a∂xu = 0, −∞ < x < ∞, t > 0 and u(x, 0) = u0(x), (1) with a > 0 a constant. Discretize the x–t plane by choosing a mesh width ∆x and time step
∆t and define the discrete mesh points (xj, tn) by
xj = j∆x, j = …, −1, 0, 1, 2, … and tn = n∆t, n = 0, 1, 2, …
(a)(2 points) Show that the following difference scheme is notstable:
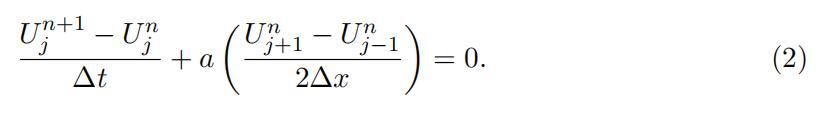
We will now derive a stable scheme.
(b)(1 point) From (1) it is clear that ∂tu = −a∂xu. Show that ∂ttu =a2∂xxu.
(c)(2points) Using the Taylor series expansion of u(x, t + ∆t) around t and question (b), show that
u(x, t + ∆t) = u(x, t) − ∆ta∂xu(x, t) + 1 (∆t)2a2∂xxu(x, t) + h.o.t. (3)
(h.o.t = higher order terms).Fourier analysis代写
(d)(2 points)Approximating the x-derivatives in (3) by central differences, show that we obtain the following finite difference scheme:
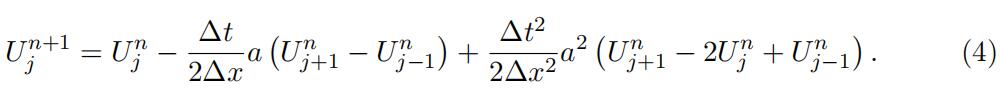
(e)(3points) Define ν = a∆t/∆x. Using Fourier analysis, find the amplification Under what condition on ν is the finite difference scheme (4) stable?

2.Given is the followingproblem:Fourier analysis代写
∂tu = ∂x (a(x)∂xu) , u(0, t) = 0, u(1, t) = 0, u(x, 0) = u0(x), where a(x) > 0. (5)
(a)(2 points) Find the finite difference scheme for (5) using the θ-method in time. You mayuse that central differences in space for the ∂x (a(x)∂xu) term is given by
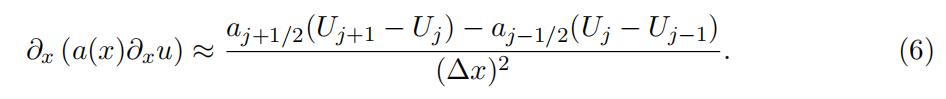
where aj+1/2 = a(xj+1/2) and xj+1/2 = 1 (xj + xj+1).Fourier analysis代写
(b)(2 points) Show that the matrix resulting from this scheme is diagonallydominant.Fourier analysis代写
(c)(5 points) Show that (6) is a consistent approximation of ∂x(a(x)∂xu).
3.(4 points) Let 0 < x < 1 and 0 < t < TFand consider the following mixed initial-boundary value problem:Fourier analysis代写
∂tu = 2∂xxu, u(0, t) = u(1, t) = 1, u(x, 0) = f (x), (7)
where f (x) = 2 if x = 0.5 and f (x) = 1 otherwise. Suppose the mesh points are chosen to satisfy
0 = x0 < x1 < x2 < … < xJ−1 < xJ = 1 Fourier analysis代写
where xj xj−1 = ∆x for all j = 1, 2, …, J. Implement the θ-method for problem (7). To solve the implicit system you need to solve a matrix system of the form AU n+1 = F . Write down the matrix A and vector F . Now compute a solution using θ = 1 and J = 10. Plot thesolution at all computed time levels between 0 and TF = 0.07 using ∆t = ∆x2 (so plot the solution at t = 0, t = ∆t, t = 2∆t, …, t = TF ).
4.(5points) The third-order Radau IA method is given by
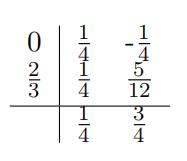
Is this Runge-Kutta method algebraically stable?
5.Beingable to capture boundary layer effects in fluid dynamics is very important and the grid plays an important role in being able to capture these effffects.
Let 0 < x < 1 and 0 < t < 10 and consider the following advection-diffusion problem:
∂tu + ∂xu − Re ∂xxu = 0, (8)Fourier analysis代写
where Re is the Reynolds number. Consider the following boundary conditions u(0, t) = 1 and u(1, t) = 0 and initial condition u(x, 0) = 1 − x. The exact steady-state solution to this problem is given by
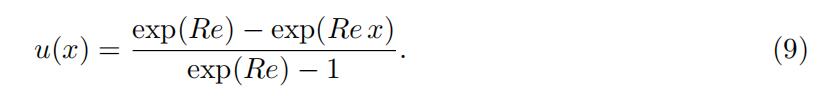
To discretize (8), we first use a uniform grid, where
xi = (i − 1)∆x, i = 1, 2, …, N + 1, (10)Fourier analysis代写
where ∆x = 1/N . As finite difference method, we use, for i = 2, 3, …, N ,
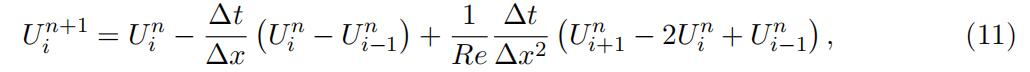
(a)(5points) Take Re = Implement the finite difference discretization (11). For this, take N = 64 and ∆t small enough such that your scheme is stable. In one figure, plot the exact steady solution given by (9) and the numerical approximation at time t = 10. At t = 10, compute the error E = maxi=1,…,N |Ui − u(xi)|. Compute this error also when N = 128. Based on these two errors, what would you say is the order of the finite difference method given by (11)Fourier analysis代写
We will now compute the solution on the following non-uniform grid:
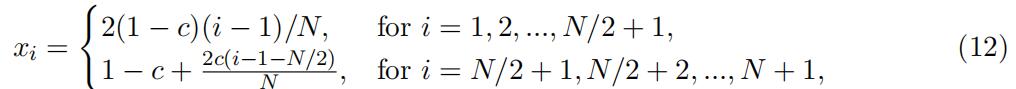
where c = (2/Re) ln(N ). The reason to use this non-uniform grid is that for high Reynolds numbers Re the solution rapidly changes in a small neighbourhood of the point x = 1. This non-uniform grid captures these changes better than a uniform grid.
A finite difference approximation to (8), on the non-uniform grid (12), is given by
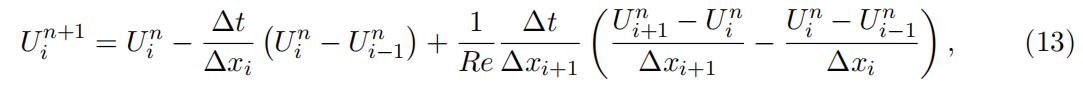
for i = 2, 3, …, N , and where ∆xi = xi − xi−1.
∆t . Σ 1 ∆t . U n − U n U n − U n Σ Fourier analysis代写
(b)(3points) Take Re = Implement the finite difference discretization (13). For this, take N = 64 and ∆t small enough such that your scheme is stable. In one figure, plot the exact steady solution given in part (a) and the numerical approximation at time t = 10. At t = 10, compute the error E = maxi=1,…,N |Ui − u(xi)|. Compute this error also when N = 128. Based on these two errors, what would you say is the order of the finite difference method given by (13)?Fourier analysis代写
(c)(1 point) Now take Re = 1000. In the same figure, plot the solution computed on the uniform grid and the solution on the non-uniform grid. Use N = 64. Explain the difference.

其他代写:考试助攻 计算机代写 java代写 algorithm代写 assembly代写 function代写paper代写 金融经济统计代写 web代写 编程代写 report代写 algorithm代写 数学代写 finance代写 作业代写 代写CS作业 python代写 code代写 Haskell代写 代码代写 Data Analysis代写
