ECMT5001: In-semester Exam (2022s1)
代考计量经济学期中 The number of Bob’s burgers sold on a day, denoted N, follows a normal distribution with mean 400 and standard deviation 50.
Time allowed: 1.5 hours
The total score of this exam is 40 marks. Attempt all questions. Correct all numerical answers to 2 decimal places.
1.[Total: 9 marks] Bob is the proud owner of the restaurant ”Hungry Bob.” The only product Hungry Bob sells is Bob’s burger, which is priced at $10 each.
The number of Bob’s burgers sold on a day, denoted N, follows a normal distribution with mean 400 and standard deviation 50.
(a) [3 marks] What is the probability that the daily revenue exceeds $5,000?
It is known that the total daily cost, denoted C, follows a normal distribution with mean $1,000 and standard deviation $300. The correlation between C and N is 0.8.Let P denote the total daily profit.
(b) [1 mark] Express P in terms of C and N.
(c) [2 marks] Compute E(P).
(d) [3 marks] Compute V ar(P).

2.[Total: 16 marks] The government reported that the infection rate of COVID-19 is 0.2. 代考计量经济学期中
Let Y denote the number of people infected with COVID-19 in a random sample of 5 individuals.
(a) [3 marks] What is the distribution of Y ? Name the distribution and specify its parameter(s).
(b) [3 marks] Compute P(Y > 1).
(c) [4 marks] Compute P(Y > 2jY > 1).
(d) [6 marks] Simon wanted to test whether the true infection rate is higher than 0.2. 代考计量经济学期中
He collected a random sample of 100 individuals. It was found that 27 individuals were infected with COVID-19. Carry out a hypothesis test for Simon at the 5 percent significance level. Show all your steps. A complete response should include:
i.setting up the null and alternative hypotheses;
ii.defining an appropriate test statistic;
iii. stating the distribution of your test statistic under the null hypothesis;
iv.computing the test statistic based on the sampled data;
v.making a decision using a correct method (e.g., critical value approach or p-value approach); and
vi.drawing a conclusion.
3.[Total: 15 marks] Carol is a trader for an investment bank in Wall Street. 代考计量经济学期中
She is studying the tick movement of a blue chip stock. Let X denote the price change (in number of ticks).
The probability density function of X is given below.
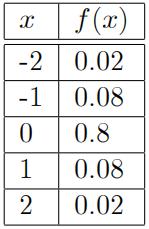
(a) Compute the following:
i.[2 marks] E(X)
ii.[2 marks] E(X2 )
iii. [2 marks] sd(X)
(b) Let S denote the sign of X, defined below
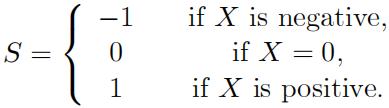
Let |X| denote the absolute value of X (e.g., |-2|= 2, |2| = 2). Note that |X| = SX and X =S |X|.
i.[3 marks] Compute Cor(S; |X|), the correlation between S and |X|.
ii.[4 marks] Compute Cor(S; X), the correlation between S and X.
iii. [2 marks] Are S and X independent? Why or why not?

更多代写:加拿大代考代管 代考托福 加拿大Cs代上网课 会计Essay代写论文 毕业论文选题代写 Econometrics期中代考
