代考宏观计量经济学 Macroeconometrics代写

Midterm

代考宏观计量经济学 Above: the βs and &s are parameters; the ρ parameters are numbers strictly between  zero  and 1; and ηt is white noise.

Problem 1 (25 points total)

Suppose you are interested in running the following regres- sion:

y_t = β0 + β1x_t + ε_t;

where

_εt = ρ0 + ρ1ε_t–1 + ηt,

Above: the βs and &s are parameters; the ρ parameters are numbers strictly between  zero  and 1; and ηt is white noise. Derive mathematically E (ε_t). Please show your work.  

Problem 2 (25 points total).  代考宏观计量经济学

Continuing with problem 1, denote the variance of η by Then, please address the following two parts.

Part a (12.5 points). Suppose that &1 =0 but all other assumptions from problem 1 remain unchanged. What properties of white noise does “ satisfy, if any? Please show your work.   代考宏观计量经济学

Part b (12.5  points).  Continuing  with part  (a),  suppose that,  as in part  (a),  in reality  &1 = 0. However, you incorrectly assume that the equation for ” is instead exactly as in problem 1 meaning that, in particular, &1 (0; 1).  Given this assumption, you decide to use  the transformation strategy to try to solve the assumed (yet non-existent) issue of Örst order serial correlation for the purposes of running the regression noted in problem 1, that is,

y_t = β0 + β1x_t + ε_t.

Does this (ultimately incorrect) use of the transformation strategy generate any problematic issues for the purposes of estimating the transformed equation and getting at the parameters of interest? Please show your work in detail.

Problem 3 (25 points total).   代考宏观计量经济学

Let  be a k  ×   1 vector of OLS estimates that result from running a regression of the vector y on the matrix X.Show that for the k ×1 vector β of true underlying parameters we can write the sum of squared residuals, denoted SSR (β), as

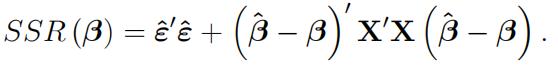
While we have generally worked with time subscripts in this class, for simplicity they are omitted in this case.  Above, is the vector of estimated residuals, and X is the matrix of regressors. Please show your work in detail.

Problem 4 (25 points total). Consider the following regressions:

y_t = 1.2y_t–1 + ε_t

and

x_t = 1.3x_t–1 – 0.4x_t–2 + t,   代考宏观计量经济学

where the error terms ε and are white noise.  Assess whether the following statement as a whole is completely true, completely false, entirely uncertain, or partly true: “Given the regressions above, it follows trivially that the equation for y is explosive because the slope parameter on the first lag of this variable is greater than 1. Similarly, because in the equation for x the slope parameter on the first lag of this variable is greater than 1, then the process governing the behavior of x is explosive as well.” Please justify your answer mathematically and in detail. An answer without mathematical justification earns zero points.

更多代写：美国哲学网课代修  雅思代考  秋季网课代上  欧美文学论文代写  纽约州立大学论文代写  Essay的结构

合作平台：essay代写 论文代写 写手招聘 英国留学生代写