ECO5204 Macroeconomics I
代考宏观经济学 Writethe Lagrangian of the problem (note: you may use either the lifetime budget constraint, or the period budget constraints.)
Midterm 1
This exam is closed-book and closed-notes. You have until the end of the class period. Please clearly indicate your final answer to each question, putting a box around key numbers or expressions. Show your work, and provide a reasonable amount of explanation for what you do and what you find. Total points are 100.
Time limit: 1 hours 15 minutes
Name:
Date:
1.Saving Problem (35 points). 代考宏观经济学
Consider the basic infinite-horizon saving prob- lem we covered in class with constant gross interest rate R and periodincome
{yt}. Assets are at, and initial assets a0 are given. Household utility is:
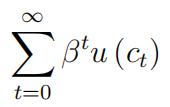
where u (·) is a strictly increasing, strictly concave function that satisfies the Inada conditions.
(a)Write the household budget constraint.
(b)Derive the lifetime budget constraint and discuss its meaning. 代考宏观经济学
(c)Formally state the optimization problem facing households.
(d)Writethe Lagrangian of the problem (note: you may use either the lifetime budget constraint, or the period budget constraints.)
(e)Solvethe problem to derive the Euler equation. 代考宏观经济学
(f)How does your solution relate to the Permanent Income Hypothesis (PIH) and the concept of consumptionsmoothing ?

2. Solow Model (20 points). 代考宏观经济学
(a)Write down the key difference equation that determines the dynamics of capital in the Solow Model.
(b)Derivea condition for steady state capital in the Solow Model.
(c)Whatis the golden rule level of capital? What is the condition for the golden rule in the Solow Model?
(d)Speakinggenerally, what are the predictions and shortcomings of the Solow Model?
3. Optimal Growth Problem with Durable Consumption Good (45 points).
Suppose that there is a representative household that maximizes utility:
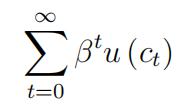
New goods are produced from capital using production function f (k). Both u (·) and f (·) are strictly increasing and strictly concave and satisfy the Inada condi- tions. Old capital depreciates at rate δ ∈ (0, 1). However, unlike in the baseline model, consumer goods are durable and also depreciate at rate δ. Consumption
goods and capital can be converted into one another one-for-one. However, it is still the case that capital is chosen in the previous period, whereas consump- tion is chosen in the period in which it is consumed. The resource constraint is
ct + kt+1 ≤ (1 − δ) (kt + ct−1) + f (kt). 代考宏观经济学
(a)Formallystate the optimal growth problem (i.e. Social Planner’s Problem).
(b)We will solve the problem What are the state variables and choicevariables?
(c)State the Bellman equation.
(d)Derive first-order and envelope conditions.
(e)Combine to derive optimality conditions. 代考宏观经济学
(f) Derive conditions for steady state.
(g) What difference does durability of the consumption good make to the steady state? Provide an intuition for your results.

