Algebra MATH-UA.0343-003
Midterm exam
代数考试代写 Problem 1. Defifine a relation on R123as follows:(x13,y1) ∼ (x2,y2) if and only if there exists λ > 0 such that (x1,y1) = (λx2,y2).
- Make sure that this fifile has your last name in its name!
- This is an open book exam: you can use lecture notes and the textbook.
- Only complete, detailed solutions will get the full credit. No credit will be given for an answer without a proof.
- Include the following pledge on the top of your fifirst page “I shall perform honestly all my academic obligations. I will not represent the words, works, or ideas of others as my own; will not cheat; and will not seek to mislead faculty or other academic offiffifficers in their evaluation of my course work or in any other academic affffairs.”
- Write you NetID (e.g. yu3) in the top right corner of every page.
Problem 1. 代数考试代写
Defifine a relation on R123as follows:
(x13,y1) ∼ (x2,y2) if and only if there exists λ > 0 such that (x1,y1) = (λx2,y2).
Prove that this is an equivalence relation, and describe the equivalence classes.
Problem 2.
Find (with a proof!) the smallest positive integer in the set
A = {24u + 60v + 150w | u, v,w ∈ Z}.
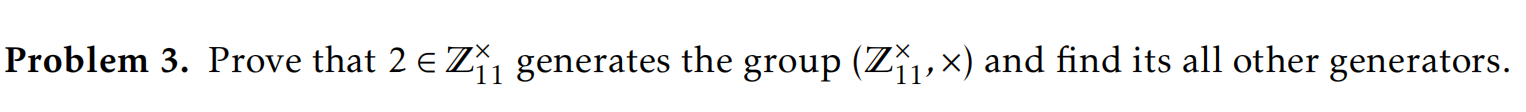
Problem 4.
Let G be an abelian group, and x,y ∈ G are two elements of orders 4. What are the possible orders
of xy ∈ G?
Problem 5. 代数考试代写
Does the set of 2 × 2 matrices
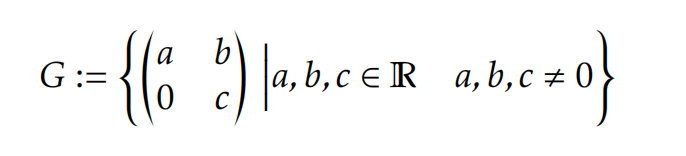
form a group with respect to the matrix multiplication?
Problem 6. 代数考试代写
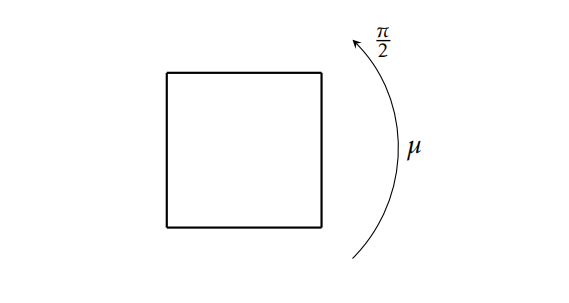
Let G be the group of rigid plane motions of a square (includes rotations and reflflections). Find
the index of the subgroup generated by the rotation µ (see the picture)

其他代写:homework代写 北美作业代写 algorithm代写 analysis代写 英国代写 Exercise代写 finance代写 C/C++代写 code代写 CS代写 cs作业代写 essay代写
