代数和微积分代写 基础数学代写

AMA1100 Basic Mathematics – An Introduction To Algebra And Differential Calculus

Assignment 2

 

A Guideline   代数和微积分代写

 Instructions for uploading the Assignment through Blackboard

1. Please download the “Assignments” from your Blackboard website in the link.

https://learn.polyu.edu.hk/webapps/blackboard/content/listContentEditable.jsp?content_id=_6350357_1&course_id=_109017_1

2. Please complete all questions.
3. Sign the covering declaration statement and write your answers with detailed steps.
4. Please scan your solutions onto a PDF using the app “CamScanner”on Google Play or Apple Store:

https://play.google.com/store/apps/details?id=com.intsig.camscanner&hl=en

OR

https://apps.apple.com/us/app/camscanner-scanner-to-scan-pdf/id388627783

You may use other app scanners, like “Tiny Scanner”, “Genius Scanner” etc.          代数和微积分代写

5. Please upload/attach your assignment solutions (a single) PDF file with the first page “covering declaration statement” at the same place you’ve downloaded this assignment by pressing the “Browse My Computer”, choosing your PDF file you want to upload, and then press Submit. You may re-submit the assignment again, to a maximum of 10 times, before the due date. Only the last attempt will be counted.

Covering Declaration：

1. have not given nor received any unauthorized aid to/from any person or persons, and
2. have not used any unauthorized materials in completing my answers to this submission

 

B Questions   代数和微积分代写

Please complete the following questions and upload the solutions through Blackboard.

Remember, combine all your solutions into one single PDF file.

 

 

4. Show that the point P(1, 1) lies on the curve defined by the equation

K : x²y + y³ = x³ + y²

and find the tangent to the curve K at P(1, 1). [8 marks]

 

 

8. A function f(x) and its first and second order derivatives f′(x) and f′′(x) are shown in the following table.    代数和微积分代写

x	f	f′	f′′
0	1	0	−π2
1	-1	0	π2

If g(x) = e^xf(x²), find the values of g(x) and its first and second order derivatives g′(x) and g′′(x) for x = 0 and x = 1.  [6 marks]

 

 

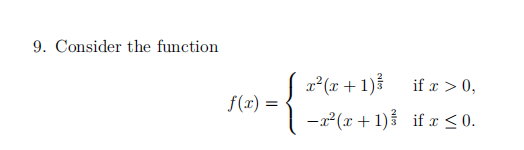
(a) Find f′(x) and f′′(x) for x = 0, −1.

(b) Discuss the existence of f′(x) and f′′(x) when x = 0, −1.

(c) Find the local maxima and minima (if any) of f(x) by the first derivative test.

(d) Find the local maxima and minima (if any) of f(x) by the second derivative test. [18 marks]

 

 

更多代写：cs澳洲春季网课代上  考试作弊  英国历史Online exam代考   澳洲英语论文代写  北美dissertation代写  现代自然科学论文代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写