EF 5070: FinancialEconometrics
Problem Set 4: Mock FinalExam
Due Dec 14th, 2018
Section A (40%)
Attempt ALL questions from this Section
1. (20 pts) Answer briefly the following questions
a) How to understand volatility? How to understand uncertain and risk?
b) Describe one test statistics that can be used to evaluate model adequacy and explain how it works using plain words.
c) Provide two reasons for the observed significant first order autocorrelation of high frequency data.
2. (20 pts) Suppose that simple return of a monthly stock index follows an AR dynamics,
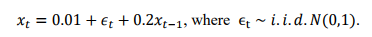
a) What is the mean of the simple return of this monthly stock?
b) What is the variance of the simple return of this monthly stock?
c) Consider the forecast origin h = 100 with
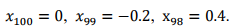
. Compute the 1-step-ahead forecast of the simple return at the forecast origin h = 100 and the variance of your forecast error.
d) Compute 2-step-ahead forecast at the forecast origin h=100.
e) Provide two features of AR models.
Section B (60%)
Attempt ALL questions from this Section
1. (30 pts) Consider the daily returns of Apple (AAPL) stock from October 1st, 2009 to September 30, 2017. Let Pt denote daily closing prices. We denote rt as the percentage log returns of daily Apply stock.
a) Provide two reasons why we prefer log returns over price levels in regression analysis.
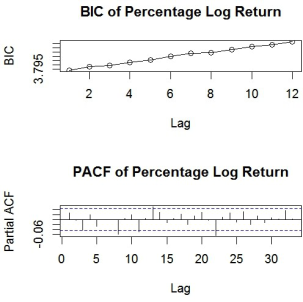
b) Based on R output Q(b), can you ensure stationarity of the return series? Provide your reasoning.
c) From the R output in appendix Q3 (c), we fit a Gaussian AR (1) model to the rt series. Do you find strong evidence on the predictability ability that lagged returns exhibit on current returns at 5% significance level? Form your hypothesis, write down the test statistics, asymptotic distribution of your test statistics, rejection rule and conclusion.
d) Now, we want to fit an MA model to the rt series. From the R output in appendix Q3 (d) and Figure Q3-1 below, what is the best MA(q) model? Why? Write down the fitted MA(q) model.
a) From the Figure Q3-2 below, do you think we should model volatility processes? Why? Now, we fit an GARCH model to the rt series. Please explain why GARCH models can capture the well-known volatility clustering effect.
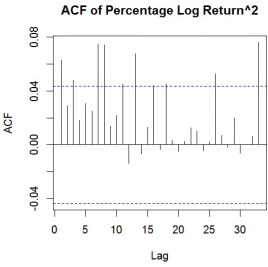
Figure Q3-2
b) Now, we will fit a GARCH(1,1) model to the return series. From R output in appendix Q3 (e)-(f), please write down the fitted model and its equivalent ARMA representation. Is the GARCH(1,1) model estimated in f) adequate?
c) From the R output in appendix Q3 (e)-(f), do you observe significant impact that historical conditional volatility may exhibit on current conditional volatility? Write down your hypothesis, test statistics, rejection rule and conclusion. Does your model satisfy stationary conditions?
1. (30 pts) We will investigate the role nonlinearity plays in our regression analysis.
a) Now, we consider another simple nonlinear model that allows us to examine asymmetric pattern in constant effect as follows,
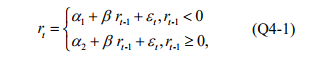
From the R output in appendix Q4 (a), write down the fitted model of (Q4-1) and provide interpretations for x .
a) Do you find statistically significant evidence for asymmetry in the constant effect at 10% level? Form your hypothesis, write down the test statistics, rejection rule and conclusion.
b) Do you find statistically significant evidence for the predictability ability that lagged one period return exhibit on current return at 5% level? Form your hypothesis, write down the test statistics, rejection rule and conclusion.
Now, we consider a two-stage Markovian chain Regime-switching model for the market model.
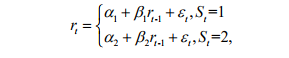
a) From the R output in appendix Q4 (d)-(f), write down the fitted model.
b) Compute the unconditional volatility of the model in stage 1 and state 2. Which regime has higher uncertainty?
c) From the R output in appendix Q4 (d)-(f), compute the expected duration for stage 1 and stage 2 respectively.
Appendix 1:
R Output Appendix
> library(quantmod)
> library(tseries)
> library(TSA)
> getSymbols(‘AAPL’,from=’2009-10-01′,to=’2017-09-30′)
[1] “AAPL”> head(AAPL)
AAPL.Open AAPL.High AAPL.Low AAPL.Close AAPL.Volume AAPL.Adjusted
| 2009-10-01 | 29.538 | 29.676 | 28.797 | 25.83714 | 131177900 | 23.16128 |
| 2009-10-02 | 28.910 | 29.632 | 28.900 | 26.41429 | 138327000 | 23.67865 |
| 2009-10-05 | 29.673 | 29.778 | 29.366 | 26.57429 | 105783300 | 23.82208 |
| 2009-10-06 | 29.919 | 30.280 | 29.848 | 27.14428 | 151271400 | 24.33305 |
| 2009-10-07 | 30.240 | 30.366 | 30.124 | 27.17857 | 116417000 | 24.36378 |
| 2009-10-08 | 30.384 | 30.510 | 30.102 | 27.03857 | 109552800 | 24.23828 |
| > tail(AAPL) |
AAPL.Open AAPL.High AAPL.Low AAPL.Close AAPL.Volume AAPL.Adjusted
| 2017-09-22 | 152.085 | 152.817 | 151.101 | 151.89 | 46645400 | 151.3459 |
| 2017-09-25 | 150.529 | 152.376 | 149.696 | 150.55 | 44387300 | 150.0107 |
| 2017-09-26 | 152.326 | 154.473 | 152.235 | 153.14 | 36660000 | 152.5914 |
| 2017-09-27 | 154.353 | 155.276 | 154.092 | 154.23 | 25504200 | 153.6776 |
| 2017-09-28 | 154.443 | 154.835 | 153.249 | 153.28 | 22005500 | 152.7310 |
| 2017-09-29 | 153.761 | 154.684 | 152.546 | 154.12 | 26299800 | 153.5679 |
> AAPLP=as.numeric(AAPL$AAPL.Close)
>
> #Form percentage log returns
> lnrt=diff(log(AAPLP))*100
> head(lnrt)
[1] 2.2091892 0.6039056 2.1222470 0.1262342 -0.5164430 0.6320077>
##Q3(b)
> #(b)
> Box.test(lnrt)
Box-Pierce test
data: lnrt
X-squared = 1.307, df = 1, p-value = 0.2529
> adf.test(lnrt,k=20)
Augmented Dickey-Fuller Test
data: lnrt
Dickey-Fuller = -9.2706, Lag order = 20, p-value = 0.01 alternative hypothesis: stationary
##Q3(c)##
> #(c)
> mc=arima(lnrt,order=c(1,0,0))
> mc
Coefficients:
ar1 intercept 0.0255 0.0888
s.e. 0.0223 0.0368
##Q3 (d)
> md=arima(lnrt,order=c(0,0,1))
> md
Coefficients:
ma1 intercept 0.0255 0.0887
s.e. 0.0223 0.0368
#Q3 (e)-(f)
> library(‘fGarch’)
> mf=garchFit(~garch(1,1),data=lnrt,trace=F)
> summary(mf)
Std. Errors:

based on Hessian Error Analysis:
Standardised Residuals Tests:
Statistic p-Value
| Jarque-Bera Test | R | Chi^2 | 1344.524 | 0 |
| Shapiro-Wilk Test | R | W | 0.9621468 | 0 |
| Ljung-Box Test | R | Q(10) | 11.66765 | 0.3079153 |
| Ljung-Box Test | R | Q(15) | 16.84009 | 0.3285136 |
| Ljung-Box Test | R | Q(20) | 20.52761 | 0.4253902 |
| Ljung-Box Test | R^2 | Q(10) | 4.954776 | 0.8941784 |
| Ljung-Box Test | R^2 | Q(15) | 9.191117 | 0.8673143 |
| Ljung-Box Test | R^2 | Q(20) | 12.17481 | 0.9099277 |
| LM Arch Test | R | TR^2 | 6.862016 | 0.8665957 |
##Q4## ##Q4(a)-(c)##
> y=lnrt[2:T]
> x=lnrt[1:(T-1)]
> idx=c(1:(T-1))[x<0]
> nsp=rep(0,(T-1))
> nsp[idx]=x[idx]
> c1=rep(0,(T-1))
> c1[idx]=1
> xx=cbind(y,x,c1,nsp)
>
> mda=lm(y~c1+x)

> summary(mda) Coefficients:
##Q4(d)-(f)##
> mod<-lm(lnrt ~ 1)
> msm_intercept <- msmFit(mod, k=2, sw=c(T,T,T), p=1)
> summary(msm_intercept) Markov Switching Model
Coefficients:
Regime 1
———
Estimate Std. Error t value Pr(>|t|)
(Intercept)(S) 0.1540 0.0386
lnrt_1(S) 0.0182 0.0328
Residual standard error: 1.063557
—
Regime 2
———
Estimate Std. Error t value Pr(>|t|) (Intercept)(S) -0.0786 0.1169
lnrt_1(S) 0.0205 0.0478
Residual standard error: 2.468642
Transition probabilities:
Regime 1 Regime 2
Regime 1 0.91144868 0.2150418
Re

